Файл: ТЭА-2009_ГЛАВА-4.doc

4.5. Законы распределения случайных величин

Законы распределения отказов, являющихся случайными величинами, имеют большое значение для теории и практики по обеспечению надежности технических систем. Значение этих законов позволяетрассчитывать и прогнозировать надежность технических систем на этапах проектирования и испытаний, производства и эксплуатации, а также при оценке правильности установления и продления ресурсов и сроков эксплуатации технических систем.

Наибольшее значение для решения задач по обеспечению надежности имеют следующие законы распределения случайных величин:

• нормальное распределение;

• экспоненциальное (показательное) распределение;

• распределение Вейбулла;

• гамма-распределение;

• закон распределения Релея;

• распределение χ².

Применение того или иного закона распределения обусловлено характеристиками появления и изменения показателей надежности по времени.

Применительно к показателям технических систем, эксплуатируемых на автомобильном транспорте и в сельском хозяйстве, в подавляющем большинстве случаев используются законы нормального распределения, экспоненциального распределения, распределения Вейбулла.

В ряде случаев законы распределения случайных величин могут быть опи­саны аналитически, как функции параметров этих законов. Такие аналитические зависимости имеются для нормального, экспоненциального и ряда других законов распределения случайных величин, описывающих процессы ТЭА.

Общий вид закона распределения:

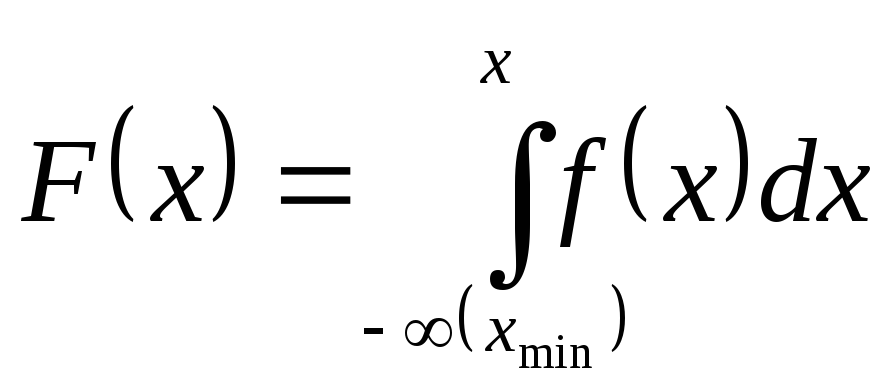; (4.20)

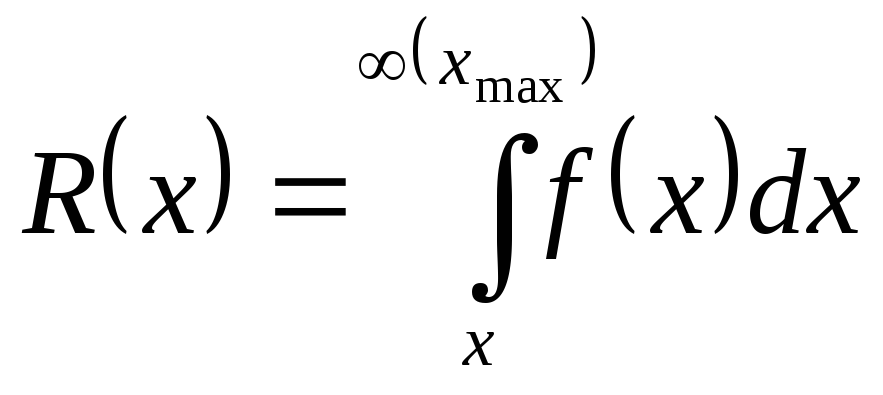, (4.21)

причем

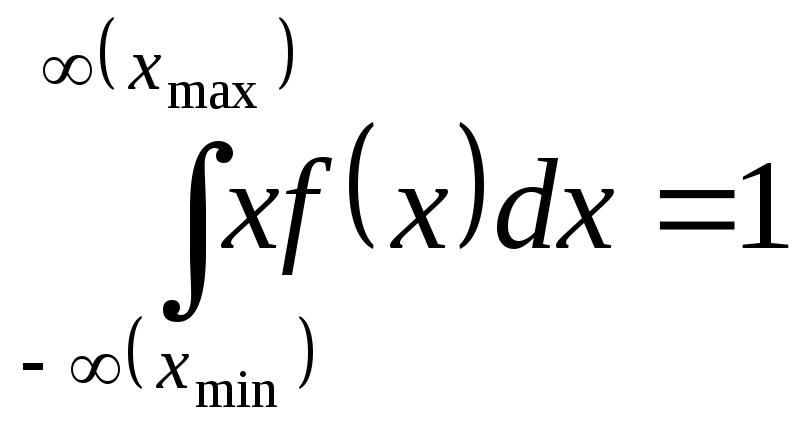, . (4.22)

4.5.1. Нормальный закон распределения (двухпараметрический: σ и х). Нормальный закон часто называют законом Гаусса. Этот закон занимает важное место и наиболее часто используется на практике по сравнению с другими законами распределения.

---

Основная особенность этого закона состоит в том, что он является предельным законом, к которому приближаются другие законы распределения. Его используют для описания постепенных отказов, корда распределение времени безотказной работы в начале имеет низкую плотность, затем максимальную плотность и далее плотность снижается, то есть нормальным распределением описывают наработки на отказ элементов и систем вследствие их износа и старения.

Нормальный закон формируется, когда на исследуемый процесс и его результат влияет сравнительно большое число независимых (или слабозависимых) элементарных факторов (сла­гаемых), каждое из которых в отдельности оказывает лишь незначительное дейст­вие по сравнению с суммарным влиянием всех остальных:

, (4.23)

. (4.24)

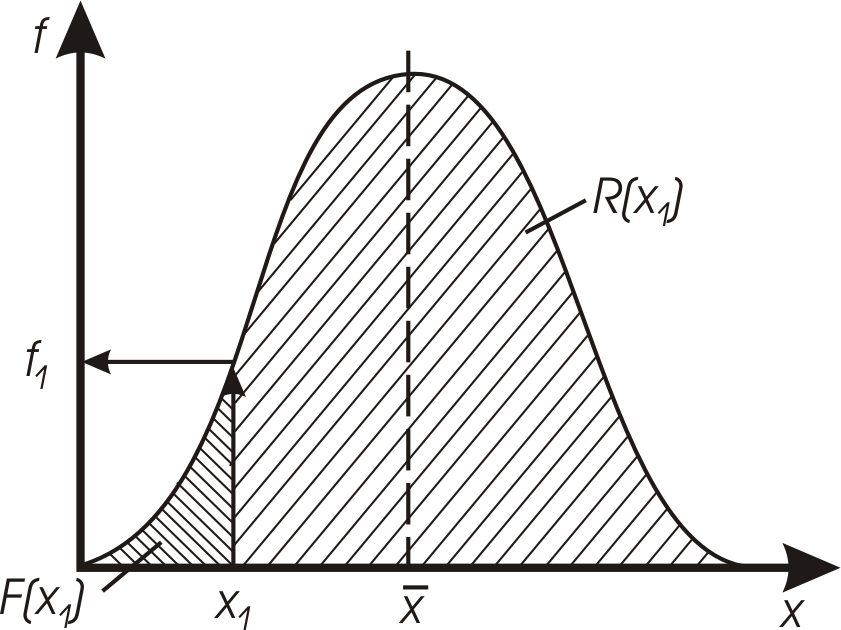
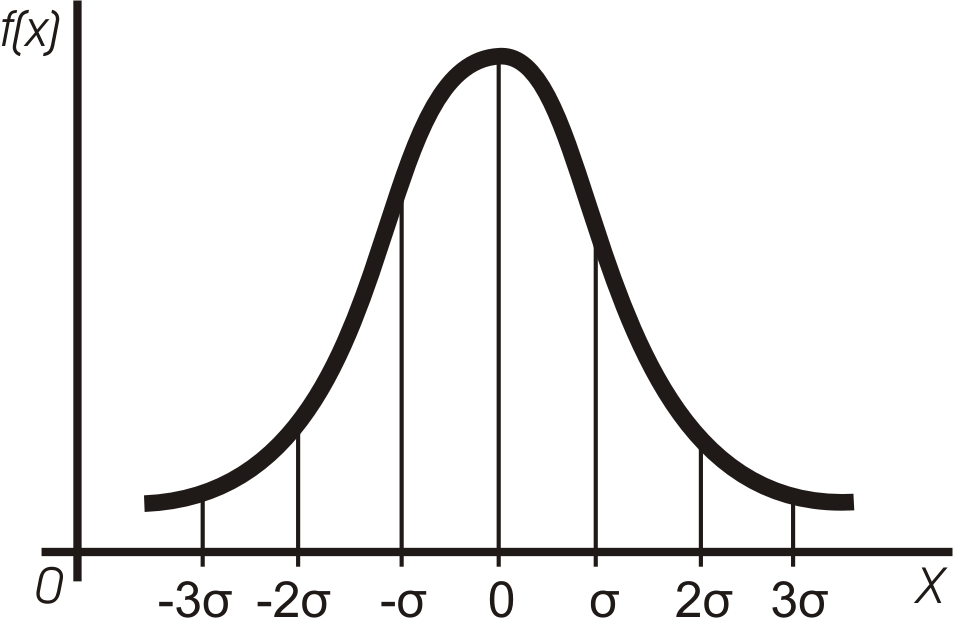
Рис. 4.6. Дифференциальная функция распре­деления - закон нормального распределения

4.5.2. Экспоненциальный закон (однопараметрический – λ) нашел широкое применение, так как он прост для практического использования. Экспоненциальный закон описывает надежность работы машины в период ее нормальной эксплуатации, когда постепенные отказы еще не проявляются и надежность характеризуется внезапными отказами.

При экспоненциальном законе распределения вероятность безотказной работы не зависит от того, сколько проработало изделие с начала эксплуатации, а определяется конкретной продол­жительностью рассматриваемого периода или пробега Δх, называемого временем выполнения задания. Таким образом, эта модель не учитывает постепенного изме­нения параметров технического состояния, например, в результате изнашивания, старения и других причин, а рассматривает так называемые нестареющие элемен­ты и их отказы. Экспоненциальный закон используется чаще всего при описании времени безотказной работы различных изделий: сложных технических систем, эксплуатируемых в период после приработки и до появления постепенных отказов; элементов электронной аппаратуры, систем управления. Кроме того, этот закон используют для описания продолжительности разнообразных ремонтных воздействий и в ряде других случаев:

---

; (4.25)

. (4.26)

Для этого закона ;;ν =1.

Рис. 4.7 – Экспоненциальный закон распределения случайной величины: а – плотность распределения; б – функция распределения

4.5.3. Закон распределения Вейбулла (двухпараметрический – а и b). Среди непрерывных распределений закон распределения Вейбулла один из наиболее часто применяемых в оценке надежности по результатам испытаний и эксплуатации. Это распределение Вейбулл использовал при описании разбросов усталостной прочности стали, пределов ее упругости, размеров частиц сажи и др. В настоящее время закон распределения Вейбулла нашел применение при описании надежности сложных технических систем, а также при изучении разбросов в сроках службы изделий различного назначения. Его используют для оценки надежности деталей и соединений автомобилей, а также для оценки надежности в процессе приработки. Закон проявляется в модели так называе­мого слабого звена. Если система состоит из группы независимых элементов, отказ каждого из которых приводит к отказу всей системы, то в такой модели рассмат­ривается распределение времени (или пробега) достижения предельного состояния системы как распределение соответствующих минимальных значений х, отдельных элементов

. (4.27)

Функция распределения этой величины может быть выражена следующей зависимостью

, (4.28)

где а и b - параметры распределения.

Примером использования распределения Вейбулла является рас­пределение ресурса подшипника качения. Этот ресурс ограничивается ресурсом одного из элементов (шарика, ролика, конкретного участка сепаратора и т.д.).

---

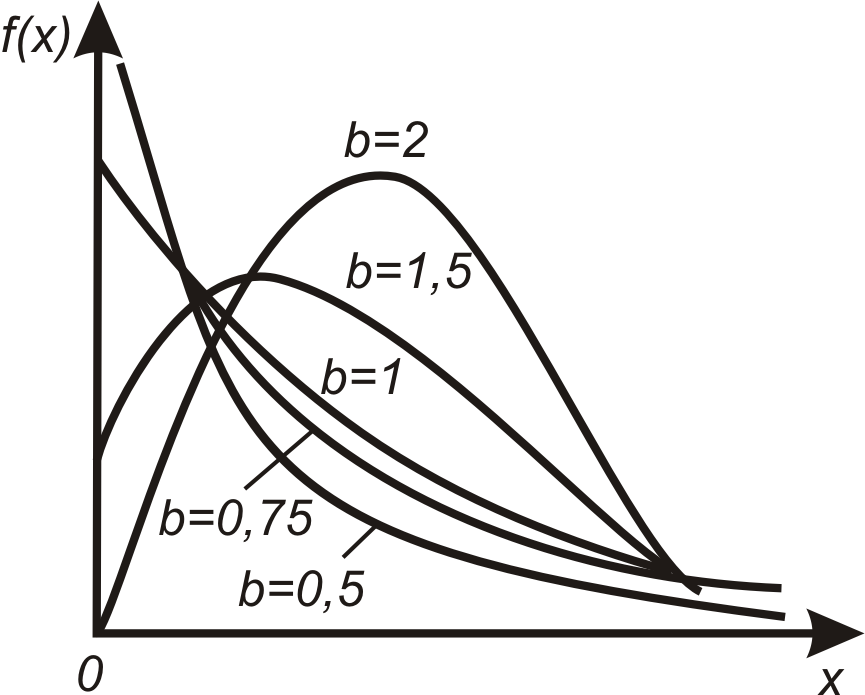
Рис. 4.8 – Кривые плотности вероятности закона распределения Вейбулла

Значение аналитических зависимостей состоит в том, что если известен вид закона (на основе опыта, литературных источников, наблюдений) и его параметры, то можно расчетными методами, не проводя объемных наблюдений, воспроизвести (прогнозировать) ожидаемые вероятности отказов и других состояний изделий и процессов. Например, для нормального закона необходимо знать два параметра (х, σ), а для экспоненциального - один (х или λ), чтобы рассчитать вероятность отказов и безотказной работы.

Теоретический закон распределения для выравнивания опытной информации ориентировочно выбирают по величине коэффициента вариации ν: если ν≤0,30, используют закон нормального распределения, если ν>0,50 – закон распределения Вейбулла, если ν=1,0 – экспоненциальный. Если значение коэффициента вариации находится в интервале 0,30…0,50, то выбирают тот закон распределения (закон нормального распределения или закон Вейбулла), который лучше совпадает с распределением опытной информации.

Таким образом, умение оценивать случайные величины позволяет в реальной эксплуатации, во-первых, перейти от ожидания стихийного появления событий (отказы изделия, требования на услуги ТО и ремонт, заправку и др.) к инструмен­тальному описанию и объективному предвидению их реализации с определенной вероятностью, что позволяет подготовить и приспособить производство к эффективному освоению соответствующих требований. Во-вторых, принять риск в качестве объективной реальности, свойственной любой деятельности, особенно эксплуатационной. Поэтому для успешной производственной деятельности важно не стремиться полностью исключить риск (что нереально для случайных процессов), а уметь его оценить и выбрать с учетом возможных отрицательных и положительных последствий.

0

0

---