Файл: ТЭА-2009_ГЛАВА-4.doc

4. Закономерности изменения

ТЕХНИЧЕСКОГО СОСТОЯНИЯ

4.1. Виды закономерностей

Процессы в природе и технике (в том числе и при технической эксплуатации) могут быть двух видов: процессы, характеризуемые функциональными зависимос­тями, и случайные (вероятностные, стохастические) процессы.

Для функциональных процессов характерна жесткая связь между функцией (зависимой переменной величиной) и аргументом (независимой переменной вели­чиной), когда определенному значению аргумента (аргументов) соответствует определенное значение функции. Например, зависимость пройденного пути от скорости и времени движения.

Случайные процессы происходят под влиянием многих переменных факторов, значение которых часто неизвестно. Поэтому результаты вероятностного процесса могут принимать различные количественные значения (т.е. наблюдается рассеивание, или вариация) и называются случайными величинами (СВ).

Случайные процессы могут быть описаны пучком кривых Y_i(t), характери­зующих изменение технического состояния конкретных изделий 1, 2, 3,..., i,..., п (рис. 4.1) от их наработки t. Иными словами, случайный процесс Y(t) может быть описан функцией, которая при каждом новом значении аргумента характеризуется набором нескольких случайных величин. Конкретные значения случайной функции при фиксированном значении аргумента t называются реализацией случайной величины.

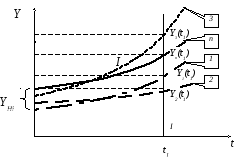
Рис. 4.1. Схема формирования случайного процесса: I – сечение случайного процесса, Y₁-Y_п – случайные величины – реализация случайного процесса Y(t) при t = t₁

При эксплуатации в основном приходится иметь дело со случайными процесса­ми и величинами.

4.2. Закономерности изменения технического состояния

автомобиля по его наработке (закономерности ТЭА

первого вида)

У значительной части узлов и деталей процесс изменения технического состоя­ния в зависимости от времени или пробега автомобиля носит плавный, монотонный характер, приводящий к возникновению так называемых постепенных отказов. При этом характер зависимости может быть различным (рис. 4.2). В случае постепенных отказов изменение параметра технического состояния конкретного изделия или среднего значения для группы изделий аналитически достаточно хорошо может быть описано двумя видами функций:

---

целой рациональной функцией n-го порядка

; (4.1)

и степенной функцией

, (4.2)

где a_o – начальное значение параметра технического состояния, l – наработка, а₁,а₂,...,а_n, b – коэффициенты, определяющие характер и степень зависимости у от l.

В практических вычислениях по формуле (4.1), как правило, достаточно использовать члены до третьего - четвертого порядков. Таким образом, зная функцию у=φ(l) и предельное Y_П или предельно допустимое Y_ПД значение пара­метра технического состояния, можно аналитически определить из уравнения l =f(у) ресурс изделия или периодичность его обслуживания (табл. 4.1).

Рис. 4.2. Возможные формы зависимости параметра технического состояния Y от нара­ботки l: Y_H, Y_П - начальное и предельное значения параметра

Таблица 4.1 - Характерные значения интенсивностей изменения

параметров технического состояния механизмов грузовых автомобилей

Наименование параметра технического состояния механизма	Единица измерения	Численное значение
Свободный ход педали сцепления	мм/1000 км	(4 - 6)·10-1
Свободный ход педали тормоза	мм/1000 км	(6 - 9)·10-1
Зазор между тормозными накладками и барабанами передних колес	мм/1000 км	(6 - 9)·10-1
Зазор между тормозными накладками и барабанами задних колес	мм/1000 км	(4 - 6)·10-1
Схождение передних колес	мм/1000 км	(1 - 3)·10-1
Прогиб ремня ременной передачи	мм/1000 км	(3 - 6)·10-1
Суммарный угловой люфт карданной передачи	град/1000 км	(1 - 3)·10-2
Суммарный угловой люфт главной передачи заднего моста	град/1000 км	(2 - 3)·10-1

---

Достаточно часто закономерности изменения параметров (например, зазора между накладками и тормозными барабанами, свободного хода педали сцепления и др.) описываются линейными уравнениями вида

, (4.3)

где a₁ - интенсивность изменения параметра технического состояния, зависящая от конструкции и условий эксплуатации изделий.

Закономерности первого вида характеризуют тенденцию изменения парамет­ров технического состояния (математическое ожидание случайного процесса), а также позволяют определить средние наработки до момента достижения предель­ного или заданного состояния.

---

4.3. Закономерности вариации случайных величин

(закономерности ТЭА второго вида)

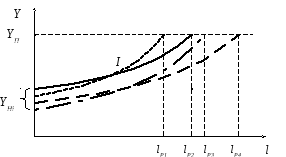
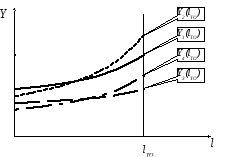
При работе группы автомобилей приходится иметь дело не с одной зависи­мостью Y(t), которая была бы пригодна для всей группы, а с индивидуальными зависимостями Y_i(t), свойственными каждому i-му изделию (рис. 4.3). Применитель­но к техническому состоянию однотипных изделий причинами вариации являются: даже незначительные изменения от изделия к изделию качества материалов, обра­ботки деталей, сборки; текущие изменения условий эксплуатации (скорость, нагрузка, температура и т.д.); качество ТО и ремонта, вождения автомобилей и др. В результате при фиксации для группы изделий определенного параметра техни­ческого состояния, например Y_П каждое изделие будет иметь свою наработку до отказа (рис. 4.3а), т.е. будет наблюдаться вариация наработки. Возникает вопрос: какую периодичность ТО планировать для группы однотипных авто­мобилей.

Если все изделия обслуживать с единой периодичностью l_ТО, то будет иметь место вариация фактического технического состояния (рис. 3б), которая скажется на продолжительности выполнения работ, количестве расходуемого материала и запасных частей.

В этом случае возникают вопросы: какую трудоемкость и стоимость операции планировать, какие потребуются производственные площади, технологическое оборудование, персонал.

При технической эксплуатации приходится сталкиваться и с другими СВ: расход топлива однотипными автомобилями даже на одинаковых маршрутах; расход запасных частей и материалов; число требований на ремонт в течение часа, смены работы поста ремонтной мастерской, станции ТО; число заездов на АЗС и др. Все это сказывается на нормировании и организации ТО и ремонта, опре­делении необходимых для этого ресурсов.

Для решения этих задач необходимо уметь оценивать вариацию СВ.

а

б

Рис. 4.3. Вариации случайных величин: а – наработки (l_P1-l_P4) при фиксации Y_П, б – параметра технического состояния (Y₁(l_ТО)-Y₄(l_ТО)) при фиксации наработки l.

---

4.4. Оценки случайных величин

Исходными данными для оценки случайных величин являются результаты наблюдений за изделиями или отчетные данные, которые выявили индивидуальные реализации случайных величин (например, наработки на отказ, фактический расход топлива, материалов и т.д.).

4.4.1. Случайные величины (от 1 до п) располагают в порядке возрастания или убывания их абсолютных значений

. (4.4)

4.4.2. Точечные оценки случайных величин:

среднее значение случайной величины

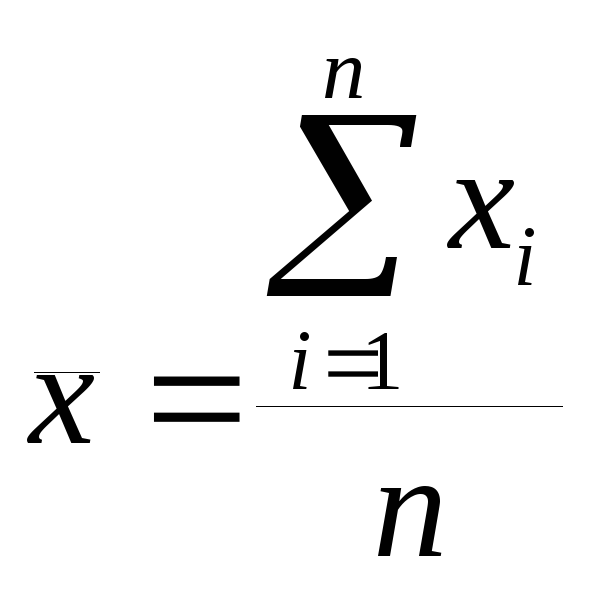; (4.5)

размах случайной величины

; (4.6)

среднеквадратическое отклонение, характеризующее вариацию,

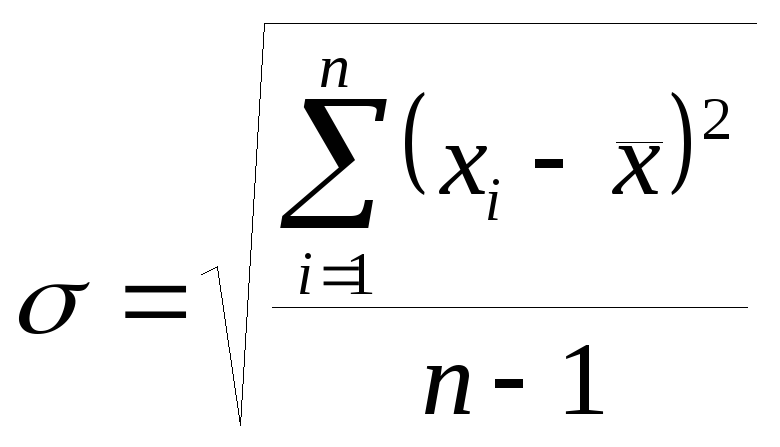; (4.7)

коэффициент вариации

. (4.8)

В ТЭА различают случайные величины

• с малой вариацией: ν < 0,1;

• со средней вариацией: 0,1≤ ν ≤ 0,33;

• с большой вариацией: ν > 0,33.

Точечные оценки позволяют предварительно судить о качестве изделий и технологических процессов. Чем ниже средний ресурс и выше вариация (σ, ν, z), тем ниже качество конструкции и изготовления (или ремонта) изделия. Чем выше коэффициент вариации показателей технологических процессов ТЭА (трудоемкость, простои в ТО или ремонте, загрузка постов и исполнителей и др.), тем менее совершенны применяемые организация и технология ТО и ремонта.

4.4.3. Вероятностные оценки случайных величин.

При вероятностных оценках рекомендуется размах СВ разбить на несколько (как правило, не менее 5…7 и не более 9…11) равных по длине Δх интервалов (табл. 4.2). Далее следует произвести группировку, т.е. определить число случайных величин, попавших в первый (n₁), второй (n₂) и остальные интервалы. Это число называется частотой. Разделив каждую частоту на общее число случайных величин (n₁+п₂+...+n_n=п), определяют частость ω_i=п_i/п. Частость является эмпирической (опытной) оценкой вероятности Р, т.е. при увеличении числа наблюдений частость приближается к вероятности ω_i→р_i.

---