ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 18.10.2024
Просмотров: 147
Скачиваний: 0
СОДЕРЖАНИЕ
Давление жидкости на плоскую наклонную стенку
Вывод уравнения Бернулли для установившегося, плавноизменяющегося потока жидкости.
9) Способы регулирования подачи центробежных насосов.
1.Водоснабжение – как отрасль народного хозяйства. Классификация систем водоснабжения.
2) Схема водоснабжения с забором из поверхностного водоисточника.
3) Схема водоснабжения с забором из подземного водоисточника.
4) Производительность и напор водопроводных насосных станций I и II подъема.
6) Определение высоты водонапорной башни.
7) Определение регулирующей емкости бака водонапорной башни.
8) Автоматический безбашенная водоподъемная установка. Схема и принцип действия.
9) Водоструйный водоподъемник, схема и принцип действия.
10) Воздушный водоподъемник (эрлифт), схема и принцип действия.
11) Требования, предъявляемые к источнику водоснабжения.
Уравнение неразрывности и его следствие:
Q= u*w=const
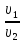 =
=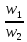
Формулы ля определения потерь напора:
hL
=λ*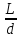 *
*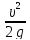 =λ*
=λ*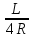 *
*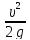 -формула
Дарси-Вейсбаха
-формула
Дарси-Вейсбаха
hм=ξ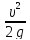 -формула
Вейсбаха
-формула
Вейсбаха
Формула Шези для равномерного движения жидкости:
υ=C*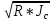 υ=
υ=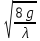 *
*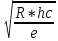 =C*
=C*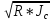
hc
= λ*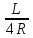 *
*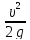
e – коэффициент Шези.
а) Формула Павловского
С=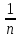 *Ry
y~1,5
*Ry
y~1,5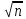 приR
< 1м
приR
< 1м
y~1,3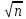 приR
> 1м
приR
> 1м
б) Формула Манинича
С=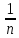 *
*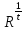
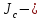 гидравлический
уклон или уклон трения, т.е. потери
приходящиеся на единицу длины.
гидравлический
уклон или уклон трения, т.е. потери
приходящиеся на единицу длины.
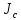 =
=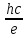
Q=
u*w=w*C*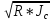 – уравнение
равномерного движения жидкости.
– уравнение
равномерного движения жидкости.
Расходная характеристика или модуль расхода
K=wc*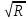 =
=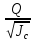
Гидравлический расчет простого трубопровода
Типы задач:
d=const
hw=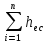 +
+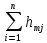
Ход решения:
Z1+
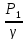 +
+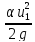 = Z2+
= Z2+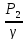 +
+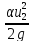
Z1=H Z2 =0
P1=Pатм P2=Pатм
υ1~ 0 υ2= ?
hw=he
+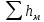 =(
λ*
=(
λ*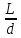 + ∑
+ ∑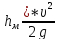
ηс=
λ*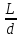 + ∑
+ ∑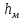
υ
=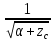 *
*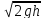 =φ*
=φ*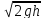
φ – коэффициент скорости
Q=
u*w=w*φ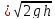 =μ*w*
=μ*w*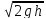
Q=μ*w*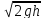
μ – коэффициент распада (φ=μ)
Если истечение происходит из закрытого резервуара в жидкую среду, то напор возрастает на высоту соответственно разности давлений:
υ=φ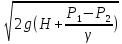
Q=μ*w*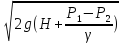
Задача №1
Определить пропускной способности трубопровода
Дано:
d;l;∆;виды местных сопротивлений;H
Определить:
Q - ?
Решение:
Q=μ*w*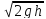
Задача №2
Определить напор необходимого для пропуска заданного расхода
Дано:
d;l;∆;виды местных сопротивлений;Q
Определить:
H - ?
Решение:
H=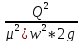
Вывод уравнения Жуковского повышения давления при гидравлическом ударе. Прямой и непрямой удар. Способы предотвращения удара.
Гидравлический удар – явление, связанное с резким изменением (повышением или понижением) давления в напорном трубопроводе при быстром изменении скорости движения жидкости в нем.
Гидравлический удар, начинающийся с волны повышенного давления, называют положительным, а с волны пониженного давления – отрицательным.
Может возникать вследствие резкого закрытия или открытия задвижки.
Вывод уравнения Жуковского повышения давления при гидравлическом ударе.
Определяем изначальную фазу гидравлического удара. Фаза гидравлического удара – время пробега прямой ударной волны(повышения давления от задвижки до резервуара) и обратной ударной волны (понижения давления от резервуара до задвижки).
Определяется
по формуле:
T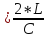
где T – фаза гидравлического удара; L – длина трубопровода; С – скорость распределения ударной волны.
Теория гидравлического удара была разработана профессором Н.Е.Жуковским. При этом были получены, проверены и рекомендованы к практическому использованию формулы для определения величины повышения давления ∆р при гидравлическом ударе и формулы для определения скорости С распространения ударной волны: ∆р=ρ*С*υ
где ρ- плотность жидкости; υ – средняя скорость движения жидкости в трубопроводе до гидравлического удара.
Величина С определяется по формуле:
C
=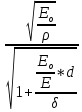
где
Е- модуль объемной упругости жидкости,
ρ- плотность жидкости,
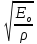 -
скорость распространения звука в
жидкости, Ео- модуль упругости
материала стенок трубы,d- диаметр трубы, δ- толщина стенок трубы.
-
скорость распространения звука в
жидкости, Ео- модуль упругости
материала стенок трубы,d- диаметр трубы, δ- толщина стенок трубы.
Для
воды отношение
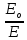 зависит
от материала труб и может быть принято;
для стальных - 0.01; чугунных - 0.02; ж/б -
0.1…0.14; асбестоцементных - 0.11; полиэтиленовых
– 1…1.45
зависит
от материала труб и может быть принято;
для стальных - 0.01; чугунных - 0.02; ж/б -
0.1…0.14; асбестоцементных - 0.11; полиэтиленовых
– 1…1.45
Прямой и непрямой удар.
В зависимости от соотношения времени закрытия задвижки tз и фазы удара Т различают прямой и непрямой гидравлический удар.
Прямой гидравлический удар может иметь место в трубопроводах весьма большой длины, когда tз < Т.Максимальное повышение давления определяется по формуле Н.Е.Жуковского.
∆р=ρ*С*υ
Непрямой гидравлический удар наблюдается когда tз >Т.При этом максимальное повышение давления:
∆р=ρ*С*υ*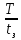
В случае, когда уменьшение скорости в трубе происходит не до нуля, а до значения υ1 возникает неполный гидравлический удар и по формуле Н.Е.Жуковского приобретет вид
∆р=ρ*С*(υ – υ1)
Способы предотвращения удара.
Исходя из формулы Жуковского (определяющей увеличение давления при гидроударе) и величин, от которых зависит скорость распространения ударной волны, для ослабления силы этого явления или его полного предотвращения можно уменьшить скорость движения жидкости в трубопроводе, увеличив его диаметр.
Для ослабления силы этого явления следует увеличивать время закрытия затвора
Истечение жидкости из отверстий и насадков. Вывести формулу истечения жидкости через малое отверстие в тонкой стенке в атмосферу. Значение коэффициентов скорости, сжатия, расхода.
Малое отверстие – отверстие линейный размер которого не более 0,1 H
H – напор над центром тяжести отверстия
d < 0,1 H
Тонкая стенка – стенка, если ее толщина не более 0,2 диаметра отверстия
δ < 0,2 d
Острая кромка стенки:
δ =(2…2,5) d
Вывести формулу истечения жидкости через малое отверстие в тонкой стенке в атмосферу.
Составим уравнение Бернулли
Z1+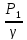 +
+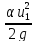 =Z2+
=Z2+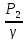 +
+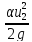
Учитывая что:
Z1=H Z2 =0
P1=Pатм P2=Pатм
υ1~ 0 υ2= ?
hм=ξ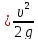
Уравнение Бернулли приобретет следующий вид:
H=
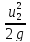 + ξ
+ ξ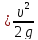
Откуда
скорость в сжатом сечении определиться
по формуле:
υ2
=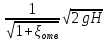
Выражение
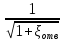 называют
коэффициентом скорости φ
называют
коэффициентом скорости φ
φ
=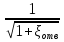
Тогда скорость истечения жидкости
υ2=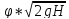
Расход жидкости Q=υ*wсж с учетом коэффициента сжатия ε и скорости υ2 может быть представлен в виде:
Q=
ε* φ*w*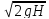
Произведение коэффициентов ε и φ принято называть коэффициентом расхода μ:
μ= ε * φ
Тогда формулу расхода окончательно можно записать так:
Q=
μ *w*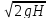
Сжатие струи оценивается коэффициентом сжатия ε;
ε
=
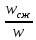
Значение коэффициентов скорости, сжатия, расхода.
Коэффициент сжатия ε;
ε
=
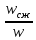
Коэффициент скорости φ
φ
=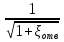
Скорость истечения реальной жидкости меньше идеальной из-за вязкости и трения, поэтому коэффициент скорости φ всегда меньше единицы.
Коэффициент расхода μ:
μ= ε * φ
Действительный расход всегда меньше расхода идеальной жидкости, следовательно, коэффициент расхода всегда меньше единицы из-за сжатия струи и трения.
Классификация насадков. Почему при том же напоре и диаметре отверстия и насадка расход насадка больше, чем отверстия
Классификация насадков.
Гидравлическим насадком называется короткий напорный патрубок, присоединенный к отверстию в тонкой стенке, длина которого составляет (3…5)d отверстия.
У внешнего цилиндрического насадка (насадок Вентури) струя жидкости непосредственно после входа в него образует сжатое сечение С - С, а вытекает полным сечением (ε=1). Внешний цилиндрический насадок увеличивает расход по сравнению с отверстием в тонкой стенке в 1,32 раза, благодаря вакууму в сжатом сечении, который обуславливает подсос жидкости.
Гидравлические сопротивления во внутреннем цилиндрическом насадке (насадок Борда) больше, чем во внешнем благодаря наличию встречных токов жидкости на входе в насадок. Это приводит к уменьшению расхода жидкости, поэтому, как правило, внешние цилиндрические насадки предпочитают внутренним.
Для конического сходящегося насадка коэффициент расхода зависит от угла конусности.
Конический расходящийся насадок характерен малой выходной скоростью. Основная особенность насадка – образование значительных разряжений в узком сечении, что существенно увеличивает расход жидкости.
Коноидальный насадок по форме внутренней поверхности близок к поверхностям вытекающей струи. Струя, выходящая из коноидального насадка, обладает еще большей, чем в сходящемся насадке, удельной кинетической энергией, т.к. гидравлические сопротивления в нем малы и расход повышен.
Почему при том же напоре и диаметре отверстия и насадка расход насадка больше, чем отверстия
Возрастание расхода жидкости наблюдается при истечении из насадков по сравнению с обычным отверстием того же диаметра. Это объясняется возникновением вакуума в начале насадка. По условию неразрывности скорость в сечении 1-1 будет меньше скорости в сжатом сечении с-с, поэтому гидродинамическое давление в сжатом сечении будет меньше давления на выходе из насадка. Поскольку в выходном сечении давление равно атмосферному, то в сжатом сечении будет наблюдаться вакуум.