ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 19.10.2024
Просмотров: 63
Скачиваний: 0
СОДЕРЖАНИЕ
8. Обработка результатов прямых измерений многократных измерений при большом числе наблюдений.
8.1 Определение систематической погрешности.
8.2 Построение укрупненного статического ряда
8.3 Определение статических характеристик рассеяния измерений.
8.4 Проверка результатов измерений на наличие грубых погрешностей
8.6.Определение погрешности измерений
8.7. Определение числа измерений для частичного и полного исключения случайной погрешности
Определяем третий центральный момент выборки
μ3=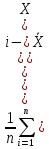 ≈
≈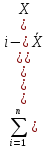 Nj
Nj
Для нашего случая имеем
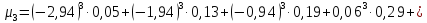
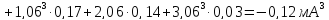
Для относительной характеристики асимметрии используют безразмерный коэффициент асимметрии
γ3=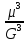 ≈
≈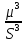
Для
нашего случая 
γ3=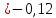 /
/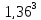 =
0,048
=
0,048
Четвертый центральный момент выборки характеризует остро- или плосковершинность кривой распределения
μ4=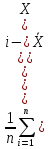 ≈
≈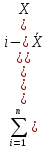 Nj
Nj
Для нашего случая пользуясь таблицей 8.3, находим
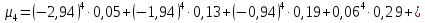
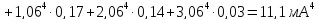
Относительное значение четвёртого нейтрального момента называется коэффициентом экцесса и находим его по формуле
γ4=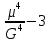 ≈
≈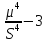
Эксцесс определяем по формуле
ξ=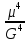 ≈
≈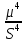
В нашем случае
γ4=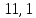 /
/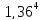 -3=
0,26
-3=
0,26
ξ=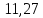 /
/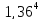 =
3,26
=
3,26
Для классификации распределений по их форме удобней использовать другую функцию от эксцесса-контрэксцесс
Kэ=1/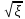
Для нашего случая
Kэ=1/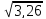 =0,52
=0,52
Таким образом получены все основные характеристики эпмирического распределения.
8.4 Проверка результатов измерений на наличие грубых погрешностей
Проверяем анормальность результатов наблюдений. Для этого берём крайние точки выборки и определяем зависимость.
U1=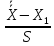 ; Un=
; Un=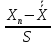

Для нашего случая
U1=(100-97,06)/ 1,36 =2,16<h=3,28
U100=(100,06-100)/ 1,36 =0,044<h=3,28
8.5 Подбор теоретического распределения погрешности
8.5.1 Построение эмпирического распределение погрешности
Для нашего примера по таблице 8.3 построим гистограмму и для наглядного представления формы закона распределения погрешностей.
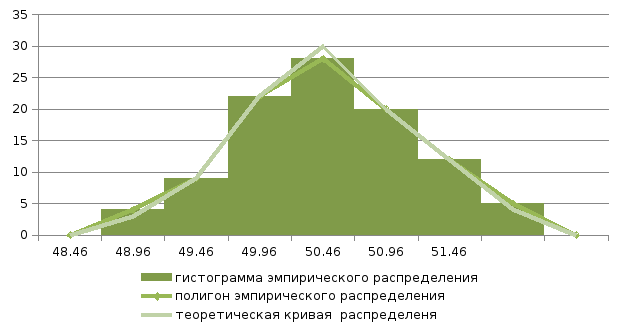
Рис.8.1. Распределение погрешностей
8.5.2 Идентификация закона распределения при помощи критерия согласия
|
Наименование закона распределения |
Асимметрия γ3 |
Эксцесс ξ |
Контрэксцесс Kэ |
|
Нормальный |
0 |
3 |
0,577 |
|
Треугольный (Симпсона) |
0 |
2,4 |
0,645 |
|
Равномерный |
0 |
1,8 |
0,745 |
|
Арксинусный |
0 |
1,5 |
0,816 |
В нашем случае при Kэ=0,66, ξ=2,286.
8.5.3
Идентификация закона распределения
при помощи критерия согласия
Tj=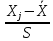
Определяем теоретическую дифференциальную функцию распределения для каждого класса по формуле
Нормальное распределение
P*(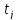 )=
)=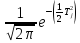
Распределение Лапласа
P*(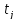 )=
)=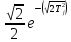
Определение дифференециальных функций для экспоненциальных
распределений.
Pj(Xj)=Pj(tj)
Для закона распределения Симпсона
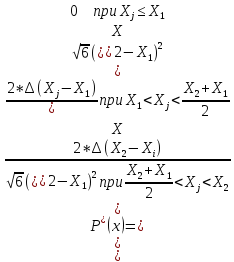
За
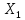 и
и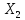 примем
точки пересечения с осью абсцисс
полигона,
примем
точки пересечения с осью абсцисс
полигона,
т.е
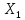 =48,21мА,
=48,21мА,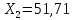 мА
мА
После расчета функции Pj(Xj) для всех законов распределения определяем теоретическую частоту для всех классов и заполняем таблицу 8.3
Ej= Pj(Xj)n.
Определяем величину χ2
χ2=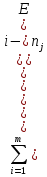
Для удобства расчета сводим все в таблицу 8.3. Находим что для нормального распределения χ2=5,6548, распределения Лапласа χ2=16,0615 ,а для распределения Симпсона χ2=22,5304 .Чем меньше χ2, тем больше подходит распределение.
Далее определяем число степеней свободы эмпирического ряда
v=m-1-r,
v=7-3=4
По
таблице П5, в соответствии с значением
v,
определяем строку и по строке смотрим
, какая из цифр vнаиболее
близко к значению χ2,
определяем столбец и вероятность
согласия эмпирического и теоритического
распределений. Таким образом, вероятность
согласия для нормального закона
распределения Р 0,95;
Лапласа Р=0;Симпсона Р=0. Наиболее
подходящим из анализируемых распределений
является нормальное распределение
(ЗНР).
0,95;
Лапласа Р=0;Симпсона Р=0. Наиболее
подходящим из анализируемых распределений
является нормальное распределение
(ЗНР).
8.6.Определение погрешности измерений
Определяем границы доверительного интервала случайной погрешности измерений:
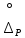 =±tp
=±tp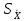
где tp – квантиль распределения
Для
нормального распределения, если n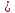 30
при Р=0,9 t0,9=1,64,при
Р=0,95 t0,95=1,96,
при Р=0,99 t0,99=2,58.
Для распределения Лапласа при Р=0,99
t0,9=1,38,
при Р=0,95 t0,95=1,87.
Для распределения Симпсона -
30
при Р=0,9 t0,9=1,64,при
Р=0,95 t0,95=1,96,
при Р=0,99 t0,99=2,58.
Для распределения Лапласа при Р=0,99
t0,9=1,38,
при Р=0,95 t0,95=1,87.
Для распределения Симпсона -
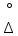 =±2,4S
=±2,4S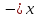 ,
,
В нашем примере
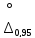 =±1,96*
=±1,96*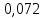 =±
0,14112
мА
=±
0,14112
мА
Далее
определяем доверительные границы не
исключённой систематической погрешности
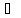 .
.
В
качестве границ не исключенной
систематической погрешности принимаем
погрешности изготовления меры
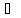 =±0,9мА.
=±0,9мА.
Определяем
доверительные границы суммарной
погрешности результата измерения
зависят от соотношения
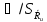
Если
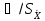 <8,
то границы погрешности результата
измерения принимаются равными случайной
погрешности,
<8,
то границы погрешности результата
измерения принимаются равными случайной
погрешности, ∑=
∑=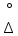
Если
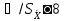 ,
то границы погрешности результата
измерения принимаются равными случайной
погрешности,
,
то границы погрешности результата
измерения принимаются равными случайной
погрешности, ∑=
ϴ
∑=
ϴ
Если0,8
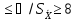 ,
то границы погрешности результата
измерения определяют по формуле
,
то границы погрешности результата
измерения определяют по формуле ∑=KS∑
∑=KS∑
K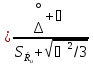
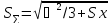
Для нашего примера
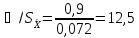
 ∑=
ϴ=0,9мА
∑=
ϴ=0,9мА
Результат измерения записываем в виде
Q=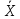 ±
±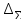 ,
приP=0,9%
,n=100
,
приP=0,9%
,n=100
A= (100,0±0,9) , при P=0.9% ,n=100
8.7. Определение числа измерений для частичного и полного исключения случайной погрешности
При
использования однократного наблюдения
(n=1)
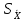 =0,75
Н ,тогда
=0,75
Н ,тогда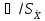 =0,9/0,75=1,2
т.е на результат однократного измерения
оказывает влияние случайная погрешность
=0,9/0,75=1,2
т.е на результат однократного измерения
оказывает влияние случайная погрешность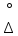 .
Число измерений для исключения
.
Число измерений для исключения определяем следующим образом.
определяем следующим образом.
Для частичного исключения
nч=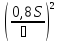
nч= (0,8*0,75)²/0,9=0,44
Для полного
nп=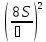
nп= (8*0,75)²/0,9=44,44
Для нашего примера при nч≥1,47 , принимаем 2 ; при nп≥ 147,5, принимаем 150
8.8. Выводы
1.Результат измерения А=(100±0,9)мА, при Р=0,9%,n=100.
2. На большую погрешность оказывает влияния как случайная, так и систематическая погрешность измерения.
3.Для частичного исключения влияния случайной погрешности нужно проводить2 и более измерений, а для полного- свыше 107.
4. Эмпирическое распределение погрешности измерений образцовой величины z совпадает с знаком нормального распределения. Это свидетельствует о малом количестве влияющих факторов на погрешность измерений.
5. Результирующие данные расчета представлены в табл. 11.14.
Таблица 11.14.
Параметры распределения и погрешности измерения
|
Параметры распределения погрешности |
Р,% |
n |
R,мА |
d,мА |
|
S,мА |
|
|
|
|
Полученные значения |
95 |
100 |
3 |
0,5 |
50 |
0,72 |
0,072 |
49,96 |
49,96 |
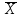 ,мА
,мА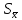 ,мА
,мА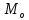 ,мА
,мА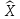 ,мА
,мА