ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 19.10.2024
Просмотров: 61
Скачиваний: 0
СОДЕРЖАНИЕ
8. Обработка результатов прямых измерений многократных измерений при большом числе наблюдений.
8.1 Определение систематической погрешности.
8.2 Построение укрупненного статического ряда
8.3 Определение статических характеристик рассеяния измерений.
8.4 Проверка результатов измерений на наличие грубых погрешностей
8.6.Определение погрешности измерений
8.7. Определение числа измерений для частичного и полного исключения случайной погрешности
8. Обработка результатов прямых измерений многократных измерений при большом числе наблюдений.
При проведении проверки рабочего средства измерений проводили прямые многократные измерения образцовой величины Z в количестве n=100 раз. Действительное значение измеряемой величины усиливалось в К раз, поэтому при её определении требуется корректировка на величину множителя φ. Доверительная вероятность расчётов Р=9%.
Исходные данные приведены в таблицах 8.1 и 8.2
Таблица 8.1
|
Показатель |
Значения |
|
Образцовая величина Z |
50 |
|
Погрешность образцовой величины |
±0,1 |
|
Единица измерения |
мА |
|
Множитель к показанию прибора φ |
0,5 |
Таблица 8.2
|
Показания прибора при проверке |
Количество повторения показания прибора |
|
97 |
5 |
|
98 |
13 |
|
99 |
19 |
|
100 |
29 |
|
101 |
17 |
|
102 |
14 |
|
103 |
3 |
Полученные
данные располагают в порядке возрастания
97,97,97,97,98,98,98,98,98,98,98,98,98,99,99,99,99,99,99,99,99,99,99,99,99,99,99,99,99,99,99,99,99,99,99,100,100,100,100,100,100,100,100,100,100,100,100,100,100,100,100,100,100,100,100,100,100,100,100,100,100,100,100,101,101,101,101,101,101,101,101,101,101,101,101,101,101,101,101,101,101,101,101,102,102,102,102,102,102,102,102,102,102,102,102, 103,103,103,103,103 мА.
8.1 Определение систематической погрешности.
В
общем случае, если известна величина
Z,
воздействующая на прибор, с точностью
в три и более раз превышающей точность
самого прибора (например, образцовая,
эталонная), то систематическую погрешность
определяем по формуле
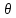 =
=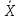 -Z
-Z
где
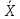 -
среднее арифметическое значение
неисправленного ряда наблюдений, В
-
среднее арифметическое значение
неисправленного ряда наблюдений, В
Среднее
арифметическое значение неисправленного
ряда наблюдений определяем по формуле
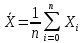
В нашем случае значение неисправленного ряда наблюдений:
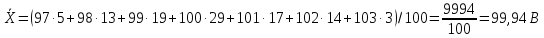
Тогда систематическая погрешность
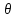 =99,94-100
= -0,06 В
=99,94-100
= -0,06 В
Систематическая
погрешность должна быть исключена из
результатов измерений путём введения
поправки, равной
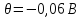
После введения поправки получается исправленный ряд значений
97,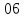 ;
97,
;
97,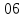 ;
97,06; 97,06; 97,06; 98,06; 98,06; 98,06; 98,06; 98,06; 98,06; 98,06;
98,06; 98,06; 98,06; 98,06; 98,06; 98,06; 99,06; 99,06; 99,06; 99,06;
99,06; 99,06; 99,06; 99,06; 99,06; 99,06; 99,06; 99,06; 99,06; 99,06;
99,06; 99,06; 99,06; 99,06; 99,06; 100,06; 100,06; 100,06; 100,06;
100,06; 100,06; 100,06; 100,06; 100,06; 100,06; 100,06; 100,06;
100,06; 100,06; 100,06; 100,06; 100,06; 100,06; 100,06; 100,06;
100,06; 100,06; 100,06; 100,06; 100,06; 100,06; 100,06; 100,06;
100,06; 101,06; 101,06; 101,06; 101,06; 101,06; 101,06; 101,06;
101,06; 101,06; 101,06; 101,06; 101,06; 101,06; 101,06; 101,06;
101,06; 101,06; 102,06; 102,06; 102,06; 102,06; 102,06; 102,06;
102,06; 102,06; 102,06; 102,06; 102,06; 102,06; 102,06; 102,06;
103,06; 103,06; 103,06; В
;
97,06; 97,06; 97,06; 98,06; 98,06; 98,06; 98,06; 98,06; 98,06; 98,06;
98,06; 98,06; 98,06; 98,06; 98,06; 98,06; 99,06; 99,06; 99,06; 99,06;
99,06; 99,06; 99,06; 99,06; 99,06; 99,06; 99,06; 99,06; 99,06; 99,06;
99,06; 99,06; 99,06; 99,06; 99,06; 100,06; 100,06; 100,06; 100,06;
100,06; 100,06; 100,06; 100,06; 100,06; 100,06; 100,06; 100,06;
100,06; 100,06; 100,06; 100,06; 100,06; 100,06; 100,06; 100,06;
100,06; 100,06; 100,06; 100,06; 100,06; 100,06; 100,06; 100,06;
100,06; 101,06; 101,06; 101,06; 101,06; 101,06; 101,06; 101,06;
101,06; 101,06; 101,06; 101,06; 101,06; 101,06; 101,06; 101,06;
101,06; 101,06; 102,06; 102,06; 102,06; 102,06; 102,06; 102,06;
102,06; 102,06; 102,06; 102,06; 102,06; 102,06; 102,06; 102,06;
103,06; 103,06; 103,06; В
8.2 Построение укрупненного статического ряда
Для удобства обработки результатов наблюдений построим укрупненный статический ряд.
Определяем область изменения признака (размах выборки):
R=Xmax-Xmin
где Xmax и Xmin – наибольшее и наименьшее показание прибора при измерениях
Для нашего примера
R=103,07-97,07=6 В
Определяем число классов (интервалов) укрупненного статического ряда m:
mmin=0,55n0,4 mmax=1,25n0,4
Для нашего примера
mmin=3,47 mmax=7,88
Рекомендуется брать нечетное число интервалов и не менее пяти. Примем m=7
Определяем
ширину класса (интервал):
d=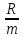 , при условииdm≥R
, при условииdm≥R
Значение d округляем в большую сторону со значащими цифрами, как и у выборки (или в два раза точнее). В нашем случае точность оценки d может быть 1,0 и 0,5 В (примем 0,5). Тогда
d=6/7=0,86 тогда d=1,0 мА
Строим
таблицу укрупненного статистического
ряда (таблица 8.1). В первой строке таблицы
записываем номера классов укрупненного
ряда 1…j…m.
Во второй строке располагаем наибольшее
и наименьшее значение результатов
наблюдений для каждого класса. Наименьшее
значение первого класса приравниваем
к наименьшему значению выборки: Xmin
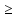 Ximin;
наибольшее значение первого класса
получается так: X₁min+d=Xjmax.
Для всех классов последовательность
выбора повторяем.
Ximin;
наибольшее значение первого класса
получается так: X₁min+d=Xjmax.
Для всех классов последовательность
выбора повторяем. 
|
Номер
класса m |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
Σ |
|||||||||
|
Границы |
Xj min |
96,56 |
97,56 |
98,56 |
99,56 |
100,56 |
101,56 |
102,56 |
- |
||||||||
|
класса |
Xj max |
97,56 |
98,56 |
99,56 |
100,56 |
101,56 |
102,56 |
103,56 |
- |
||||||||
|
Средняя точка класса Xj |
97,06 |
98,06 |
99,06 |
100,06 |
101,06 |
102,06 |
103,06 |
- |
|||||||||
|
Частота nj |
5 |
13 |
19 |
29 |
17 |
14 |
3 |
100 |
|||||||||
|
Относительная частота Nj |
0,05 |
0,13 |
0,19 |
0,29 |
0,17 |
0,14 |
0,03 |
1 |
|||||||||
|
(Xj-X) |
-2,94 |
-1,94 |
-0,94 |
0,06 |
1,06 |
2,06 |
3,06 |
- |
|||||||||
|
Nj(Xj-X)² |
0,43 |
0,49 |
0,17 |
0,0014 |
0,19 |
0,29 |
0,28 |
1,8514 |
|||||||||
|
Nj(Xj-X)³ |
-1,27 |
-0,95 |
-0,16 |
0,0000 |
0,2 |
1,2 |
0,86 |
-0,12 |
|||||||||
|
Nj(Xj-X)⁴ |
3,74 |
1,84 |
0,15 |
0,0000 |
0,22 |
2,52 |
2,63 |
11,1 |
|||||||||
|
tj |
2,16 |
1,42 |
0,69 |
0,044 |
0,78 |
1,5 |
2,25 |
- |
|||||||||
|
Нормальное распределение |
P*(tj) |
0,04 |
0,147 |
0,32 |
0,40 |
0,30 |
0,131 |
0,0325 |
- |
||||||||
|
Pj=(d/s)P*(tj) |
0,029 |
0,11 |
0,24 |
0,29 |
0,222 |
0,097 |
0,024 |
|
|||||||||
|
Ej=Pjn |
0,145 |
1,43 |
4,56 |
8,41 |
3,77 |
1,4 |
0,072 |
|
|||||||||
|
|(Ej-nj|) |
|
|
|
|
|
|
|
|
|||||||||
|
(nj-Ej)²/Ej |
|
|
|
|
|
|
|
|
|||||||||
|
Распределение Лапласа |
P*(tj) |
|
|
|
|
|
|
|
|
||||||||
|
Pj=(d/s)P*(tj) |
|
|
|
|
|
|
|
|
|||||||||
|
Ej=Pjn |
|
|
|
|
|
|
|
|
|||||||||
|
|(Ej-nj|) |
|
|
|
|
|
|
|
|
|||||||||
|
(Ej-nj)²/Ej |
|
|
|
|
|
|
|
|
|||||||||
|
Распределение Симпсона |
P*(Xj) |
|
|
|
|
|
|
|
|
||||||||
|
Pj=(d/s)P*(tj) |
|
|
|
|
|
|
|
|
|||||||||
|
Ej=Pjn |
|
|
|
|
|
|
|
|
|||||||||
|
|(Ej-nj|) |
|
|
|
|
|
|
|
|
|||||||||
|
(Ej-nj)²/Ej |
|
|
|
|
|
|
|
|
|||||||||
Таблица
8.3 




45
КР.53.12.38. 08
Лист
Частота
в nj
в j-м
классе – это попавшее в интервал
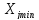 ≤
≤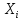 ≤
≤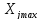 значения
значения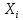 выборка 1…i…n.
Заполняется пятая строка таблицы 8.3 При
этом сумма частот:
выборка 1…i…n.
Заполняется пятая строка таблицы 8.3 При
этом сумма частот:
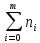 =n
=n
В нашем случае 4+9+22+28+20+12+5=100
Относительная частот Nj записываем в шестой строке таблицы и определяем так
Nj=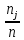
Поэтому
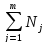 =1,0
=1,0
8.3 Определение статических характеристик рассеяния измерений.
Далее определяем выборочное среднее арифметическое (точнее оценка первого нейтрального выбора μ₁ или математического ожидания M(X))
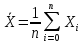 ≈
≈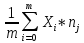 ≈
≈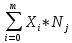
В нашем случае после введения поправки выборочное среднее
арифметическое для исправленного ряда наблюдений должно быть равно Z
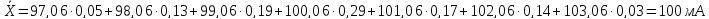 Мода
M0
в выборке – значение, которому
соответствует максимум частоты. В нашем
случае M0=
Xj=4=100,06
(см. табл. 8.3)
Мода
M0
в выборке – значение, которому
соответствует максимум частоты. В нашем
случае M0=
Xj=4=100,06
(см. табл. 8.3)
Медиана
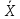 в выборке - результат наблюдения - среднее
место в вариационном ряду. Обычно медиана
определяется так
в выборке - результат наблюдения - среднее
место в вариационном ряду. Обычно медиана
определяется так
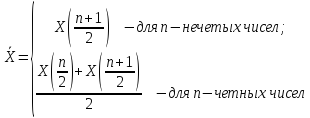
В нашем случае n/2=50; (n+2)/2=51; по вариационному ряду
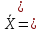 100,06
+100,06)/2=100,06 В
100,06
+100,06)/2=100,06 В
Определяем точечную оценку дисперсии
S2=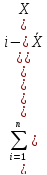 ≈
≈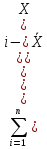 Nj.
Nj.
Для нашего случая пользуясь таблице 8.3 имеем
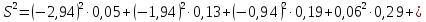
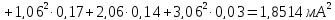
Так как дисперсия имеет квадратичную размерность для большей наглядности пользуются средним квадратическим отклонением (СКО), точечная оценка которого определяется по формуле
S=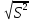
В нашем случае
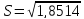 =1,36
мА
=1,36
мА
Точечная
оценка СКО среднего арифметического
значения определяется по выражению
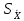 =
=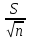
Для нашего случая
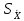 =
=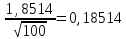 В
В