ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 28.02.2019
Просмотров: 6238
Скачиваний: 1

ХХ-й век – «новая физика»:
теория относительности
квантовая теория
Полная энергия и импульс частицы определяются
соотношениям:
E = mc
2
γ, p = γmv = E/(c
2
v).
Полная энергия и импульс частицы зависят от
системы отсчета.
1900 г.
– М. Планк
- гипотеза о квантовой природе теплового
излучения: вещество, как совокупность гармонических
осцилляторов различной частоты.
3
3
8
1
( , )
exp(
/
) 1
h
U T
h
kT
c
Масса не меняется при переходе от одной инерциальной системы отсчета к другой.
Она является лоренц-инвариантом. Полная энергия, импульс и масса связаны
соотношением:
E
2
- p
2
c
2
= m
2
c
4
Постоянная Планка
h=6.625∙10
-27
эрг∙с=6,625∙10
-34
Дж∙сек = 4,14∙10
-21
МэВ∙сек
1905 г.
-
А.Эйнштейн
– СТО
1905 г.
-
А.Эйнштейн
– электромагнитное излучение состоит из квантов:
,
( / )
(
, 1929 .)
E
h
p
h
n
фотон Герберт Льюис
г
1905 г.
-
А.Эйнштейн
– электромагнитное излучение состоит из квантов:
,
( / )
(
, 1929 .)
E
h
p
h
n
фотон Герберт Льюис
г
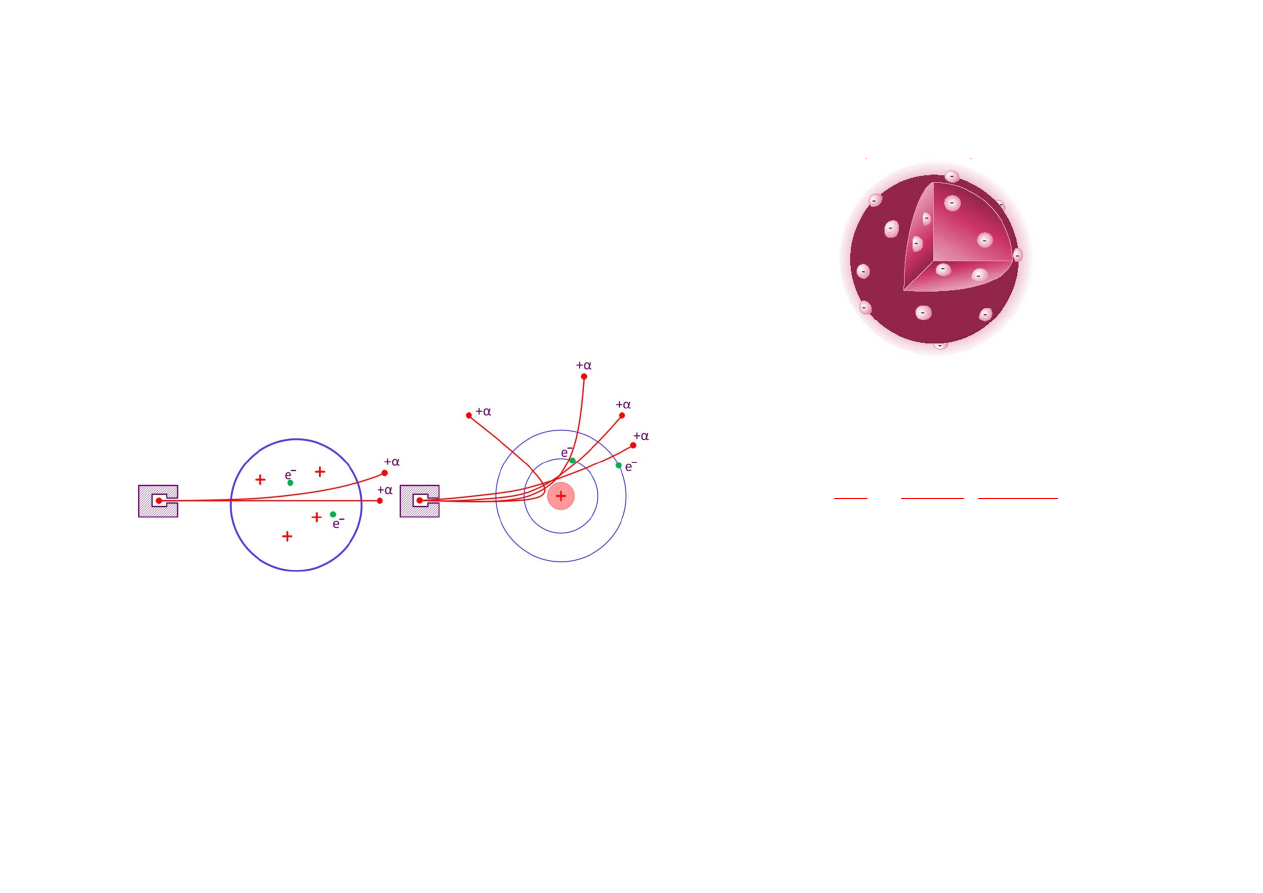
1906 г.
–
модель
атома Томсона
1905 г.
-
А.Эйнштейн
– электромагнитное излучение состоит из квантов:
,
( / )
(
, 1929 .)
E
h
p
h
n
фотон Герберт Льюис
г
1906 г.
–
модель
атома Томсона
1911 г.
– Э.Резерфорд
– планетарная модель атома.
2
1
2
4
1
4
sin
/ 2
Z Z e
d
d
T
Формула Резерфорда:
Проблема – нельзя объяснить стабильность атомов.
1905 г.
-
А.Эйнштейн
– электромагнитное излучение состоит из квантов:
,
( / )
(
, 1929 .)
E
h
p
h
n
фотон Герберт Льюис
г
1906 г.
–
модель
атома Томсона
1911 г.
– Э.Резерфорд
– планетарная модель атома.
2
1
2
4
1
4
sin
/ 2
Z Z e
d
d
T
Формула Резерфорда:
Проблема – нельзя объяснить стабильность атомов.
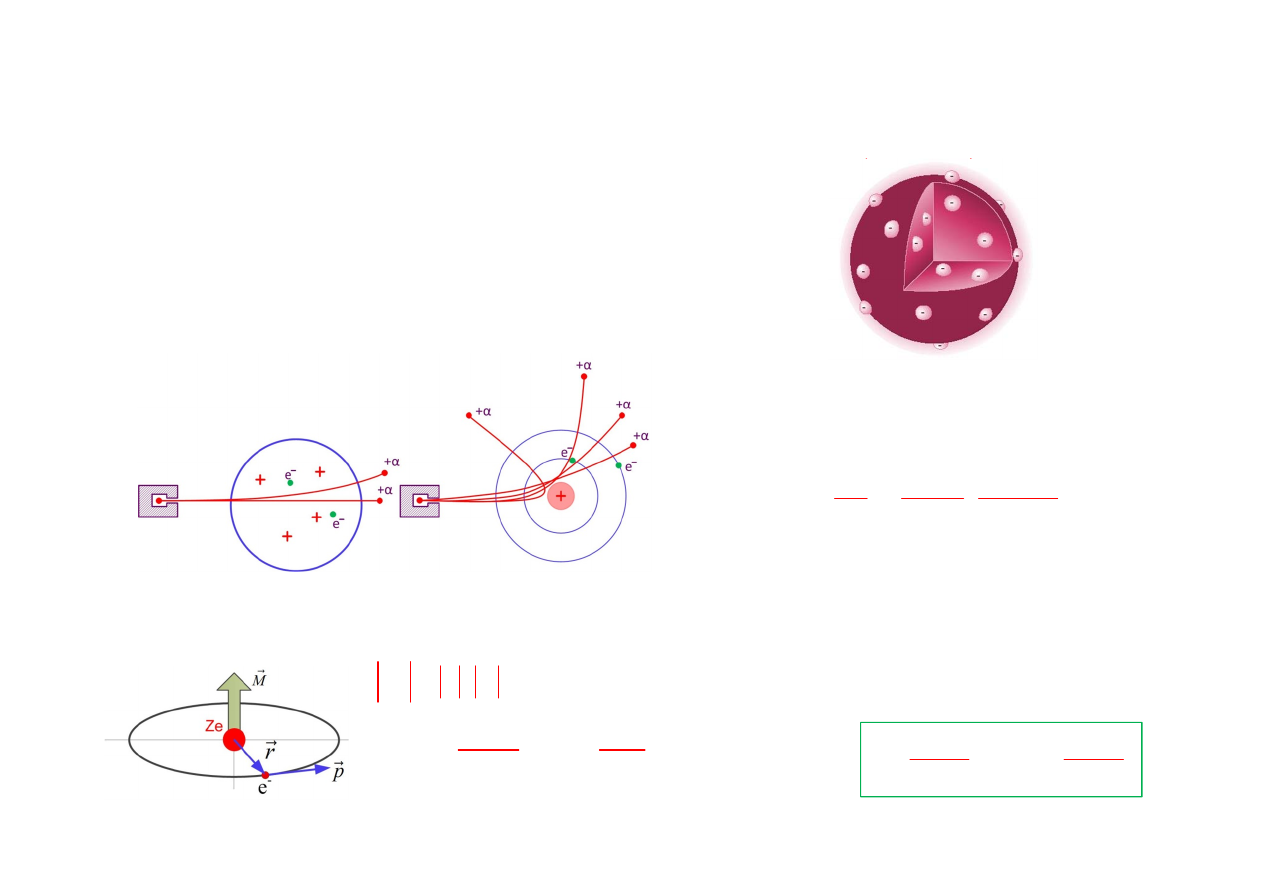
1913
г. – квантовая модель атома
Н.Бора →
квантование момента количества движения
2
2
2 4
2
2
2
;
2
,
e
e
n
n
e
n
z e
r
E
ze m
n
(
/ 2 ;
/ 2 ),
M
r
p
mvr
n
h
2
2
2
2
(
)
кул
ц
Ze e
mv
F
F
mrv
Ze
r
r