ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 28.02.2019
Просмотров: 6274
Скачиваний: 1
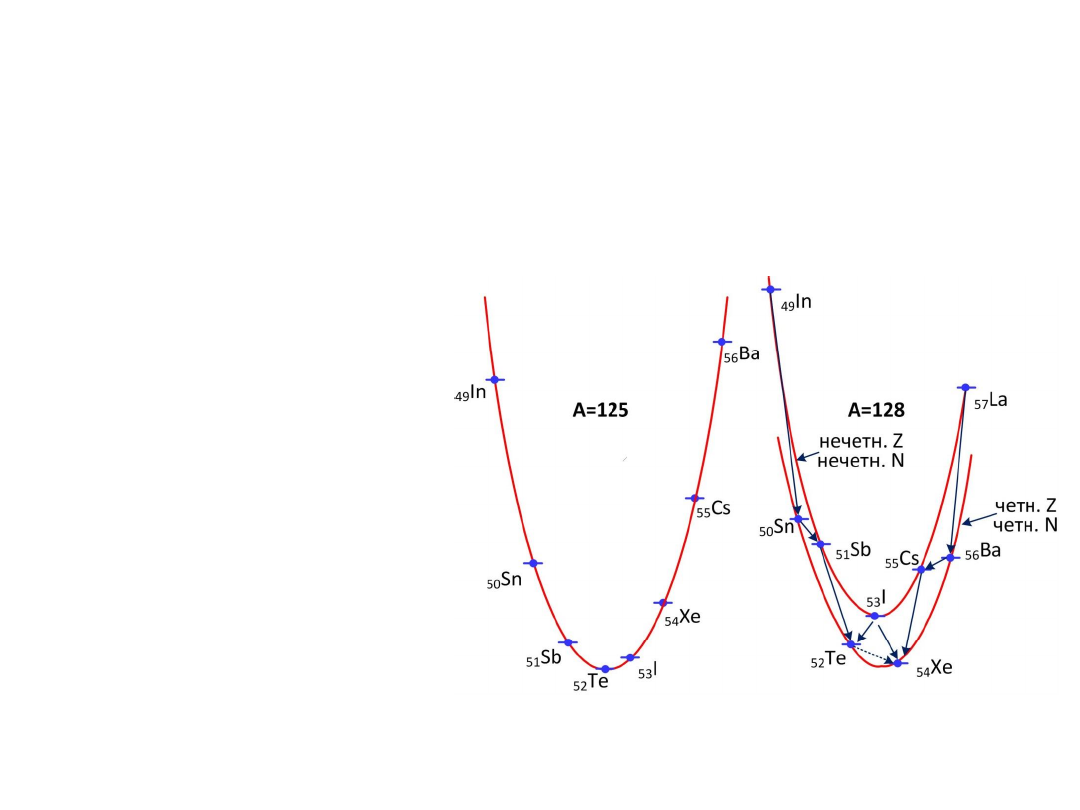
β-превращения ядер
.
На левом рисунке - парабола масс для ядер с нечетным
A = 125.
125
In,
125
Sn,
125
Sb
подвержены
β
-
-
распаду,
125
I,
125
Xe,
125
Cs,
125
Ba
-
β+
-
распад. Чем больше энергия
β
-
распада ядер (разность масс между
соседними изобарами), тем они
дальше от линии стабильности.
Для
нч-нч и ч-ч
ядер – две параболы.
При данном
A
, стабильных
ч-ч
ядер может быть несколько
(например,
136
Xe,
136
Ba,
136
Ce
).
Ядра с
нечетным Z
редко имеют
больше одного стабильного
изотопа.
β-превращения ядер
.
В результате β-распада →
три частицы
: конечное ядро и два лептона.
Энергия, сообщаемая ядру в силу его большой массы, мала, и ею можно
пренебречь.
Кинетическая энергия, выделяющаяся при β-распаде практически целиком
уносится парой лептонов, причем распределение энергий между ними
может быть любым → энергетический спектр позитронов (электронов) и
нейтрино (антинейтрино) непрерывен в интервале от
0 до Q
β
.
Спектр энергий продуктов е-захвата – дискретен. Можно определить
импульс нейтрино.
e
n
p e
N
ν
(E) = N
e
(Q
β
– E)
Теория β-распада
.
1934 г. - основы теории β–распада – Э.Ферми.
1958
г. - универсальная
4-
фермионная теория слабых взаимодействий
→ элементарный процесс слабого взаимодействия представляет собой
локальное взаимодействие четырех фермионов, т.е. частиц с
полуцелыми спинами.
В настоящее время процессы как слабого, так и электромагнитного
взаимодействия находят объяснение в новой теории - объединенной
теории электрослабых взаимодействий.
В теории Ферми предполагалось, что взаимодействие, которое приводит к
бета распаду, мало по сравнению с взаимодействием, которое формирует
состояния ядра. Это позволило использовать теорию возмущений и
записать вероятность распада в единицу времени
в виде (золотое
правило Ферми):
2
*
,
(2 / ) |
|
fi
f
fi
f
fi
i
гд
M
V
е
M
E
dv
Теория β-распада
В начальном состоянии – ядро с волновой функцией
φ
i
.
В конечном –
φ
f
,
φ
е
, φ
ν
.
Считаем, что продукты распада не взаимодействуют друг с другом:
Ферми предположил: существует некоторое поле (слабое) с константой
взаимодействия
G
F
.
В первом приближении матричный элемент можно
заменить следующим
/
,
/
e
exp
ipr
exp
iqr
*
*
*
f
f
e
fi
f
e
fi
i
M
V
dv
*
*
*
fi
F
f
e
i
M
G
dv
Плотность состояний свободного движения электрона и нейтрино:
2
2
3
3
1 4
4
( , )
(2
)
(2
)
p dp
q dq
p q
dQ
Пренебрегая энергией отдачи ядра:
Q
β
=T
e
+T
ν
, dQ
β
=dT
e
=d T
ν
Полагая
m
ν
= 0:
q = (Q
β
- T
e
)/c, dq = dT
ν
/c.
p = [T
e
(T
e
+ 2mc
2
)]
1/2
/c, c
2
pdp = (T
e
+ mc
2
)dT
e
ρ(E) ~ p(T
e
+ m
e
c
2
)(Q
β
- T
e
)
2
dT
e
Теория β-распада
*
exp
(
) /
fi
F
f
i
M
G
i p
q r
dr
Было сделано
предположение
m
ν
= 0
→
в
высокоэнергетической части спектра электронов
dN
e
/dT
e
→0
.
dN
e
(Q
б
,T
e
) ~ |M
fi
|
2
[T
e
(T
e
+ 2m
e
c
2
)]
1/2
(T
e
+ m
e
c
2
)(Q
β
- T
e
)
2
F(T
e
,Z)dT
e
.
Т. о., форма β-cпектра определяется как плотностью конечных состояний, так и
квадратом матричного элемента, описывающего β-распад:
Множитель
F(T
e
,Z) -
отношение вероятности
нахождения электрона в некоторой точке с учетом
поля атома
(Z
≠ 0)
к вероятности без учета поля
(Z = 0)
. Поле искажает спектр.
Однако, если
m
ν
≠0
→
для конца спектра электронов, когда энергия нейтрино мала,
нужно записать :
2
2
;
q
m T qdq
m dT
Тогда:
dN
e
(Q
β
,T
e
) ~ [T
e
(T
e
+ 2m
e
c
2
)]
1/2
(T
e
+ m
e
c
2
)(Q
β
- T
e
)
1/2
dT
e