ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 28.02.2019
Просмотров: 6263
Скачиваний: 1
Классификация элементарных частиц по группам
Все частицы сгруппированы в четыре класса:
Гамма квант:
γ
2
0
m c
Лептоны
2
2
2
,
, ,...(
0.5
;
200
105
,...)
e
e
е
v
m c
МэВ m c
m c
МэВ
Мезоны
2
2
2
,
,...
(
280
140
,
496
...)
e
к
K
m c
m c
МэВ m c
МэВ
Барионы
2
2
, ,..
(
938,3
,
939, 6
,...)
p
n
p n
m c
МэВ m c
МэВ
Характеристики этих классов частиц значительно отличаются друг от друга:
-по типу взаимодействий,
-по квантовым числам
Статистика элементарных частиц
Коллективное поведение тождественных частиц
зависит от величины спина (S – дробный или цeлый)
S
p
=1/2 S
n
=1/2
1,2
симметричная функция (для частиц с целым спином s=0,1,...)
1
антисимитричная функция (для частиц с дробным спином s= ,...)
2
дробный спин
- статистика
Ферми-Дирака.
целый спин
- статистика
Бозе-Эйнштейна
распределения
Ферми-Дирака – в одном энергетическом состоянии
не могут находиться две частицы с одинаковыми квантовыми числами
Для ядра эти правила коллективного поведения позволяют правильно
формировать заполнение нуклонами энергетических уровней
Квантовые числа
, , ,
j
n l j m
Единицы измерения энергии в микрофизике
В макро-физике используется система СИ;
в микро-физике CGSE
Энергия выражается в
эВ, кэВ, МэВ,… эрг (CGSE)
10
12
e
1
1 эВ = q 1
4,8 10
1, 6 10
эрг
300
В
CGSE
12
ат
6
24
23
Ав
12г 1
1
1 а.е.м
г
1, 6 10
г
12 число нуклонов
12
6 10
M
С
N
2
2
24
10
3
см
1 а.е.Е
1 а.е.м.
1, 6 10
г 3 10
1, 5 10 эрг = 931,5МэВ
сек
с
Единица длины
см, ферми
(10
-13
см)
Единица времени
с, мс (10
-3
), мкс (10
-6
), нс (10
-9
)
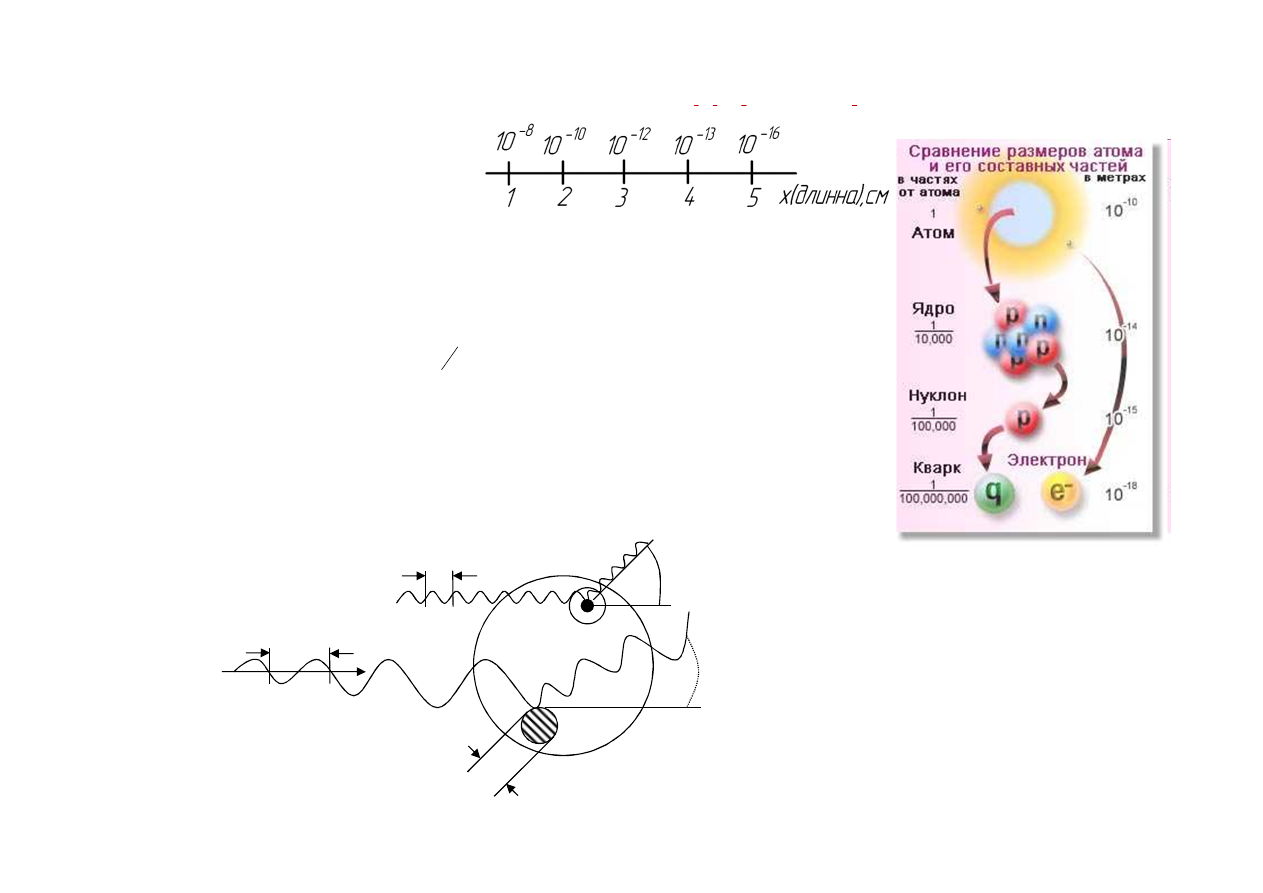
Масштабы величин в ядерной физике
8
10
-9
10
12
1
13
3
0
0
16
1
10
10
молекулы
2
-10
10
атомы
3
10
и немного меньше - характерные размеры ядра
4
10
,
1, 4
размер нуклона
5
10
кварки
уровень
уровень
уровень
уровень
Rяд
R A
R
ф
уровень
T
2
λ
λ
T P λ Rx
Зачем нужны энергии в диапазоне от доле эВ до
миллиардов МэВ
Релятивистские формулы для свободной частицы
2
2
2
2
2
формула Эйнштейна для полной энергии частицы
, где М-динамическая масса, m -масса покоя
1
, где Е полная энергия, а Т
кинетическая энергия
Импульс
=
, где
относительная скорость
1
1
E
Mc
m
М
Е
Т
mc
m
mc
V
p
MV
V
c
2
2 2
2
2
2
2
2 2
2
2
2 2
2
(
)
(
)
(
2
)
(
2
)
(
)
(
)
(
)
(
)
;
Размерность
импульса
[
]
эВ
или
эрг;
Пример записи:
10
; иначе
10
;
Если
0,
например
для
γ-кванта, то получается
E
pc
mc
pc
Т Т
mc
Т Т
mc
pc
pc
E
Т
mc
pc
mc
T
E
mc
pc
mc
mc
pc
МэВ
pс
МэВ
р
с
m
E
Т
2
0
0
2
2
0
.
Время
жизни
частицы
при
движении
возрастает
;
время
жизни
в
собственной
системе
координат
(v=0).
pc
E
T
mc
mc
mc