ВУЗ: Рязанский Государственный Педагогический Университет им. С.А. Есенина
Категория: Методичка
Дисциплина: Информатика
Добавлен: 21.10.2018
Просмотров: 1700
Скачиваний: 22
Рязанский государственный педагогический университет им С. А. Есенина
ПРАКТИКУМ
по курсу «Информатика»
Изучение табличного процессора «MS Excel» для специальностей «Социология» и «Управление персоналом»
Автор: Парадела В. Д.
Рязань 2008
Обязательная записка
Настоящий практикум подготовлен для студентов специальностей «Социология» и «Управление персоналом» с учетом дидактического принципа профессиональной направленности. При его проведении учитывается, что студенты данных специальностей уже изучили в первом семестре первого курса «MS Word», и поэтому обладают общими умениями работы с файлами прикладного пакета «MS Office». Кроме того, они также уже умеют обращаться к справочной системе, если не знают, как решить какой-то конкретный вопрос, поскольку приобретению такого навыка было уделено достаточное внимание при работе в «MS Word».
Данный лабораторный курс является пропедевтической основой изучения методов обработки результатов анкетирования. Без него не мысленно успешное обоснование нулевых гипотез в математической статистике. Но он не заменяет изучение методов обработки данных при использовании специализированных пакетов. Он только подготовит студентов к более глубокому анализу математической обработки статистических данных, показывая при этом некоторые возможности «MS Excel».
В пособии, кроме описания лабораторных работ рассматриваются основные понятия описательной и аналитической статистик. Онo создано на основе шестой главы пособия В. Я. Гельмана «Решение математических задач средствами «MS Excel»», издательство Питер, 2003.
Основные понятия и определения
«MS Excel»
-
Файл – в «MS Excel» файл называется «книгой» и имеет расширение «xls».
-
Каждая книга состоит из трех листов по умолчанию и каждый лист из 256 столбцов и 65536 строк.
-
Пересечение одного столбца и одной строки называется ячейкой.
-
Каждый столбец обозначается латинской буквой или двумя латинскими буквами от A до IV и каждая строка числом от 1 до 65536 по умолчанию.
-
Каждая ячейка имеет название, определяемое её столбцом и строкой. Например, А4, $B25, С$34 или $D$44. Знак доллара «$» фиксирует столбец или ячейку (в зависимости от его положения) при ссылках.
-
Ячейки можно заполнять автоматически при помощи маркера заполнения (маленького черного квадратика в правом нижнем углу выделенной ячейки).
-
Множество ячеек, расположенных непрерывно формирует таблицу.
-
Используя данные в таблицах можно построить диаграммы.
-
В «MS Excel» можно проводить вычисления в ячейках при помощи формул.
-
Каждая формула начинается знаком равенства «=».
-
Формулы могут создаваться пользователем. Можно также использовать встроенные формулы (Функции).
-
В «MS Excel» есть пакеты формул для специалистов разных профессии, например для социологов и специалистов, управляющих персоналом.
Мы будем изучать «MS Excel» на примере использования формул для специальностей «Социология» и «Управление персоналом».
Основные понятия и определения математической статистики
Приступая к изучению статистики в среде «MS Excel» сначала нужно смотреть определенные понятия математической статистики, методы статистического исследования, а также некоторые выборочные функции распределения и основные выборочные характеристики.
Понятие математической статистики
Раздел математики, посвященный методам сбора, анализа и обработки статистических данных для научных и практических целей, называется математической статистикой.
Математическая статистика имеет дело с массовыми явлениями. Она тесно связана с теорией вероятностей и базируется на ее математическом аппарате.
Целью статистического исследования является обнаружение и исследование соотношений между статистическими данными и их использованием для изучения, прогнозирования и принятия решений.
Статистические данные представляют собой данные, полученные в результате обследования большого числа объектов или явлений.
Математическая статистика подразделяется на две основные области: описательную и аналитическую статистику. Описательная статистика охватывает методы описания статистических данных, представления их в форме таблиц, распределений и т. п.
Аналитическая статистика или теория статистических выводов ориентирована на обработку данных, полученных в ходе эксперимента, с целью формулировки выводов, имеющих прикладное значение для самых различных областей человеческой деятельности.
Пакет «MS Excel» оснащен средствами статистической обработки данных. И хотя он существенно уступает специализированным статистическим пакетам обработки данных, тем не менее, этот раздел математики представлен в «MS Excel» наиболее полно. В него включены основные, наиболее часто используемые статистические процедуры: средства описательной статистики, критерии различия, корреляционные и другие методы, позволяющие проводить необходимый статистический анализ данных об обществе и других системах.
При рассмотрении применения методов обработки статистических данных ограничимся только простейшими и наиболее часто используемыми методами, реализованными в мастере функций и пакете анализа ««MS Excel»».
Выборочный метод
По охвату статистической совокупности исследование может быть сплошное или не сплошное. При сплошном статистическом исследовании группа наблюдения формируется путем полного охвата всех единиц изучаемого явления. Множество всех единиц наблюдения, охватываемых таким сплошным наблюдением, называется генеральной совокупностью.
Основным методом не сплошного наблюдения является выборочный метод. Если интересующая нас совокупность слишком многочисленна, либо ее элементы малодоступны, а также, если имеются другие причины (организационные, финансовые, физические и т. п.), не позволяющие изучать сразу все ее элементы, прибегают к изучению какой-то части этой совокупности. Эта выбранная для полного исследования группа элементов называется выборкой или выборочной совокупностью.
Выборка − это группа элементов, выбранная для исследования из всей совокупности элементов. Задача выборочного метода состоит в том, чтобы сделать правильные выводы относительно всего собрания объектов, их совокупности. Например, пробуя пищу, повар по одной ложке делает заключения о качестве приготавливаемого во всей кастрюле.
Конечной целью изучения выборочной совокупности всегда является получение информации о генеральной совокупности. Поэтому естественно стремиться сделать выборку так, чтобы она наилучшим образом представляла всю генеральную совокупность, то есть была бы репрезентативной или представительной. Для получения репрезентативной выборки необходимо четко определять, что понимается под генеральной совокупностью. Ее состав и численность зависят от объектов и целей проводимого исследования. Например, если мы хотим получить данные о поступающих во все вузы города, то абитуриенты данного института есть выборка из более широкой генеральной совокупности − всех абитуриентов вузов города, и эта выборка не обязательно будет являться представительной.
В тех случаях, когда генеральная совокупность недостаточно известна, обычно не удается предложить лучшего способа получения представительной выборки, чем случайный выбор. При этом случайная выборка формируется случайным отбором − из генеральной совокупности наудачу извлекается по одному объекту.
Выборочная функция распределения
По определению классическая вероятность равна отношению числа испытаний (т), в которых событие появилось, к общему количеству произведенных испытаний (п). Такая вероятность также называется статистической частотой.
На практике, сведения о законе распределения случайной величины можно получить независимыми многократными повторениями опыта, в котором измеряются значения интересующей исследователей случайной величины (варианты). На основе информации из полученной выборки можно построить приблизительные значения для функции распределения и других характеристик случайной величины.
Выборочной
(эмпирической) функцией распределения
случайной величины
![]() построенной по выборке х1, х2, ...,хn„,
называется функция Fn(x), равная доле
таких значений хi что xi <x, i= 1, ...,п.
построенной по выборке х1, х2, ...,хn„,
называется функция Fn(x), равная доле
таких значений хi что xi <x, i= 1, ...,п.
Другими словами, Fn(x) есть частота события хi < х в ряду х1,, х2,…, хn.
Связь между эмпирической функцией распределения и функцией распределения (теоретической функцией распределения) такая же, как связь между частотой события и его вероятностью: функция Fn(x )→F(x) при п → °°.
Для построения выборочной функции распределения весь диапазон изменения случайной величины X разбивают на ряд интервалов одинаковой ширины. Число интервалов обычно выбирают не менее 5 и не более 15. Затем определяют число значений случайной величины X, попавших в каждый интервал. Поделив эти числа на общее количество наблюдений п, находят относительную частоту попадания случайной величины X в заданные интервалы. По найденным относительным частотам строят гистограммы выборочных функций распределения. Если соответствующие точки относительных частот соединить ломаной линией, то полученная диаграмма будет называться полигоном частот. Кумулятивная кривая будет получена, если по оси абсцисс, откладывать интервалы, а по оси ординат − число или доли элементов совокупности, имеющих значение, меньшее или равное заданному.
При увеличении до бесконечности размера выборки выборочные функции распределения превращаются в теоретические: гистограмма превращается в график плотности распределения, а кумулятивная кривая − в график функции распределения.
В «MS Excel» для построения выборочных функций распределения используются специальная функция ЧАСТОТА и процедура пакета анализа Гистограмма.
О Функция «ЧАСТОТА» вычисляет частоты появления случайной величины в интервалах значений и выводит их как массив цифр. Функция задается в качества формулы массива. ЧАСТОТА(массив данных;массив_карманов). Здесь:
массив данных − это массив или ссылка на множество данных, для которых вычисляются частоты.
массив карманов −это массив или ссылка на множество интервалов, в которые группируются значения аргумента массив данных.
Отметим, что количество элементов в возвращаемом массиве на единицу больше числа элементов в массив_карманов. Дополнительный элемент в возвращаемом массиве содержит количество значений, больших, чем максимальное значение в интервалах.
О Процедура «Гистограмма» используется для вычисления выборочных и интегральных частот попадания данных в указанные интервалы значений. Процедура выводит результаты в виде таблицы и гистограммы.

Рис. 1.1. Пример заполнения диалогового окна Гистограмма
Параметры диалогового окна «Гистограмма» представлены на рис. 1.1.
во Входной диапазон вводится диапазон исследуемых данных;
в поле Интервал карманов (необязательный параметр) может вводиться диапазон ячеек или необязательный набор граничных значений, определяющих выбранные интервалы (карманы). Эти значения должны быть введены в возрастающем порядке. В «MS Excel» вычисляется число попаданий данных между началом интервала и соседним большим по порядку. При этом включаются значения на нижней границе интервала и не включаются значения верхней границе.
Если диапазон карманов не был введен, то набор интервалов, равномерно распределенных между минимальным и максимальным значениями данных, будет создан автоматически;
рабочее поле Выходной диапазон предназначено для ввода ссылки на левую верхнюю ячейку выходного диапазона. Размер выходного диапазона будет определен автоматически;
переключатель Интегральный процент позволяет установить режим генерации интегральных процентных отношений и включения в гистограмму графика интегральных процентов;
переключатель Вывод графика позволяет установить режим автоматического создания встроенной диаграммы на листе, содержащем выходной диапазон.
Пример 1.1. Построить эмпирическое распределение веса студентов в килограммах для следующей выборки: 64, 57, 63, 62, 58, 61, 63, 60, 60, 61, 65, 62, 62, 60, 64, 61, 59, 59, 63, 61, 62, 58, 58, 63, 61, 59, 62, 60, 60, 58, 61, 60, 63, 63, 58, 60, 59, 60, 59, 61, 62, 62, 63, 57, 61, 58, 60, 64, 60, 59, 61, 64, 62, 59, 65.
Решение
-
В ячейку А1 введите слово Наблюдения, а в диапазон А2:Е12 − значения веса студентов.
-
Выберите ширину интервала 1 кг. Тогда при крайних значениях веса 57 кг и 65 кг получится 9 интервалов. В ячейки G1 и G2 введите названия интервалов Вес и кг, соответственно. В диапазон G4:G12 введите граничные значения интервалов (57, 58, 59, 60, 61, 62, 63, 64, 65).
-
Введите заголовки создаваемой таблицы: в ячейки Н1:Н2 − Абсолютные частоты, в ячейки I1:I2 − Относительные частоты, в ячейки J1;J2 − Накопленные частоты.
-
Заполните столбец абсолютных частот. Для этого выделите для них блок ячеек Н4: Н12 (используемая функция «ЧАСТОТА» задается в виде формулы массива). С панели инструментов «Стандартная» вызовите Мастер функций (кнопка fx). В появившемся диалоговом окне Мастер функций выберите категорию Статистические и функцию ЧАСТОТА, после чего нажмите кнопку ОК. Появившееся диалоговое окно ЧАСТОТА необходимо за серое поле мышью отодвинуть вправо на 1-2 см от данных (при нажатой левой кнопке). Указателем мыши в рабочее поле Массив_ данных введите диапазон данных наблюдений (А2:Е12). В рабочее поле Двоичный массив, мышью введите диапазон интервалов (G4:G12). Последовательно нажмите комбинацию клавиш Ctrl+Shift+Enter. В столбце Н4:Н12 появится массив абсолютных частот.
-
В ячейке Н13 найдите общее количество наблюдений. Табличный курсор установите в ячейку Н13. На панели инструментов Стандартная нажмите кнопку Автосумма. Убедитесь, что диапазон суммирования указан правильно (Н4:H12), и нажмите клавишу Enter. В ячейке Н13 появится число 55.
-
Заполните столбец относительных частот. В ячейку 14 введите формулу для вычисления относительной частоты: =Н4/Н$13. Нажмите клавишу Enter. Протягиванием (за правый нижний угол при нажатой левой кнопке мыши) скопируйте введенную формулу в диапазон I5:I12. Получим массив относительных частот.
-
Заполните столбец накопленных частот. В ячейку J4 введите вручную значение относительной частоты из ячейки I4 (0,036364). В ячейку J5 введите формулу: =J4 +I5. Нажмите клавишу Enter. Протягиванием (за правый нижний угол при нажатой левой кнопке мыши) скопируйте введенную формулу в диапазон J6:12. Получим массив накопленных частот.
-
В результате после форматирования получим таблицу, представленную на рис 1.2.
-
Наблюдения
Вес
Абсолютные
Относи-
Накопленные
63
61
кг
частоты
тельные
частоты
58
58
частоты
60
60
57
2
0,036364
0,036364
59
64
58
6
0,109091
0,145454909
60
60
59
7
0,127273
0,272727636
59
59
60
10
0,181818
0,454545818
61
61
61
9
0,163636
0,618182182
62
64
62
8
0,145455
0,763636727
62
62
63
7
0,127273
0,890909455
63
59
64
4
0,072727
0,963636727
57
65
65
2
0,036364
1,000000364
55
Рис. 1.2. Результат вычислений относительных и накопленных частот из примера 1.1
-
Постройте диаграмму относительных и накопленных частот. Щелчком указателя мыши по кнопке на панели инструментов вызовите Мастер диаграмм. В появившемся диалоговом окне выберите вкладку Нестандартные и тип диаграммы График/гистограмма2. После нажатия кнопки Далее укажите диапазон данных −I1:J12 (с помощью мыши). Проверьте положение переключателя Ряды в: столбцах. Выберите вкладку Ряд и с помощью мыши введите в рабочее поле Подписи оси X диапазон подписей оси X: G4:G12. Нажав кнопку Далее, введите названия осей X и У: в рабочее поле Ось X (категорий) − Вес; Ось У (значений) — Относ. частота; Вторая ось Y (значений) − Накоплен. частота. Нажмите кнопку Готово.
-
После минимального редактирования диаграмма будет иметь такой вид, как на рис. 1.3.
Р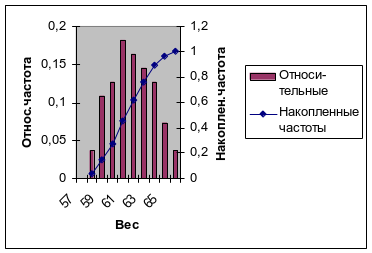
ис.
1.3.
Диаграмма относительных и накопленных
частот из примера 1.1
Пример 1.2. Для данных из примера 1.1. построить эмпирические распределения, воспользовавшись процедурой «Гистограмма».
Решение
-
В ячейку А1 введите слово Наблюдения, а в диапазон А2:Е12 − значений веса студентов.
-
Для вызова процедуры Гистограмма выберите из меню Сервис подпункт Анализ данных и в открываемся окне в поле Инструменты анализа укажите процедуру Гистограмма.
-
В появившемся окне «Гистограмма» заполните рабочие поля (см. рис. 1.1):
-
во «Входной диапазон» введите диапазон исследуемых данных (А2:Е12);
-
в «Выходной диапазон» − ссылку на левую верхнюю ячейку выходного диапазона (F1). Установите переключатели в положение Интегральный процент и Вывод графика;
После этого нажмите кнопку ОК.
В результате появляется таблица и диаграмма (рис. 1.4).
|
Карман |
Частота |
Интегральный % |
|
57 |
2 |
3,64% |
|
59,66666667 |
13 |
27,27% |
|
62,33333333 |
27 |
76,36% |
|
Еще |
13 |
100,00% |
Рис. 1.4. Таблица и диаграмма из примера 1.2
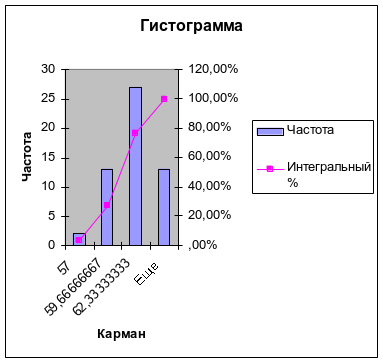
Как видно, диаграмма на рис. 1.4. несколько отличается от диаграммы на рис. 1.3. Это объясняется тем, что диапазон карманов не был введен. Количество и границы интервалов определялись в процедуре ГИСТОГРАММА автоматически. Если бы в рабочее поле Интервал карманов был бы введен диапазон ячеек, определяющих выбранные интервалы, как в примере 1.1 (57,58,59,..., 65), то полученная диаграмма была бы идентична предыдущей.
Упражнения
-
Постройте эмпирические функции распределения (относительные и накопленные частоты)для роста (в см) группы из 20 мужчин: 181, 169,178,178,171,179, 172, 181, 179, 168, 174, 167, 169, 171, 179, 181, 181, 183, 172, 171.
-
Найдите распределение по абсолютным частотам для следующих результатов тестирования в баллах; 79, 85, 78г 85, 83, 81, 95, 88 и 97 (используйте границы интервалов 70,79,89).
3. Постройте эмпирические функции распределения (абсолютные и накопленные частоты) успеваемости в группе из 20 студентов: 4,4,5,3,4,5,4,5,3,5,3,3,5,4, 5,4,3,5,3,5.
Выборочные характеристики
Замена теоретической функции распределения F(х) на ее выборочный аналог Fn(x) в определении математического ожидания, дисперсии, стандартного отклонения и т. п. приводят к выборочному среднему, выборочной дисперсии, выборочному стандартному отклонению и т. д. Выборочные характеристики являются оценками соответствующих характеристик генеральной совокупности. Эти оценки должны удовлетворять определенным требованиям. В соответствии с важнейшими требованиями, оценки должны быть:
-
несмещенными, то есть стремиться к истинному значению характеристики генеральной совокупности при неограниченном увеличении количества испытаний;
-
состоятельными, то есть с ростом размера выборки оценка должна стремиться к значению соответствующего параметра генеральной совокупности с вероятностью, приближающейся к 1;
-
эффективными, то есть для выборок равного объема используемая оценка должна иметь минимальную дисперсию.
Среди выборочных характеристик выделяют показатели, относящиеся к центру распределения (меры положения), показатели рассеяния вариант (меры рассеяния) и меры формы распределения. К показателям, характеризующим центр распределения, относят различные виды средних (арифметическое, геометрическое и т.. п.), а также моду и медиану.
Простейшим показателем, характеризующим центр выборки, является мода.
Мода − это элемент выборки с наиболее часто встречающимся значением (наиболее вероятная величина).
Средним значением выборки, или выборочным аналогом математического ожидания, называется величина
![]()
Иначе говоря, среднее значение − это центр выборки, вокруг которого группируются элементы выборки. При увеличении числа наблюдении среднее приближается к математическому ожиданию. Среднее значение обозначается также буквой М.
Выборочная медиана − это число, которое является серединой выборки, то есть половина чисел имеет значения большие, чем медиана, а половина чисел имеет значения меньшие, чем медиана. Для нахождения медианы обычно выборку ранжируют − располагают элементы в порядке возрастания. Если количество членов ранжированного ряда нечетное, медианой является значение ряда, которое расположено посередине, то есть элемент с номером (n + 1)/2. Если число членов ряда четное, то медиана равна среднему членов ряда с номерами п/2 и n/2 + 1.
Основными показатели
рассеяния вариант являются интервал
дисперсия выбор
ки, стандартное
отклонение и стандартная; ошибка.
Интервал (амплитуда, вариационный размах) − это разница между максимальным и минимальным значениями элементов выборки. Интервал является простейшей и наименее надежной мерой вариации или рассеяния элементов выборке.
Более точно отражают рассеяние показатели, учитывающие не только крайние, но и все значения элементов выборки.
Дисперсией выборки, или выборочным аналогом дисперсии, называется величина
![]()
Дисперсия выборки − это параметр, характеризующий степень разброса элементов выборки относительно среднего значения. Чем больше дисперсия, тем дальше отклоняются значения элементов выборки от среднего значения.
Выборочным стандартным отклонением (среднее квадратичное отклонение) называется величина
![]()
Это
параметр, также характеризующий степень
разброса элементов выборки относительно
среднего значения. Чем больше среднее
квадратичное отклонение, тем дальше
отклоняются значения элементов выборки
от среднего значения. Параметр аналогичен
дисперсии и используется в тех случаях,
когда необходимо, чтобы показатель
разброса случайной величины выражался
в тех же единицах, что и среднее
значение этой случайной величины. Часто
выборочное стандартное отклонение
обозначают буквой
![]() (сигма).
(сигма).
Стандартная ошибка или ошибка среднего находится из выражения
![]()
Стандартная ошибка − это параметр, характеризующий степень возможного отклонения среднего значения, полученного на исследуемой ограниченной выборке, от истинного среднего значения, полученного на всей совокупности элементов. С помощью стандартной ошибки задается так называемый доверительный интервал. 95%-ный доверительный интервал, равный х ± 2т, обозначает диапазон, в который с вероятностью р = 0,95 (при достаточно большом числе наблюдений п > 30) попадает среднее генеральной совокупности MX.
Выборочной квантилью называется решение уравнения
![]()
В. частности, выборочная медиана есть решение уравнения
![]()
Показателями, характеризующими форму распределения, являются выборочные эксцесс и асимметрия.
Эксцесс − это степень выраженности «хвостов» распределения, то есть частоты появления удаленных от среднего значений.
Асимметрия − величина, характеризующая несимметричность распределения элементов выборки относительно среднего значения. Принимает значения от -1 до 1. В случае симметричного распределения асимметрия равна 0.
Часто значения асимметрии и эксцесса используют для проверки гипотезы о том, что данные (выборка) принадлежат к определенному теоретическому распределению, в частности, нормальному распределению. Для нормального распределения асимметрия равна нулю, а эксцесс − трем.
Определение основных статистических характеристик
В результате наблюдений или эксперимента получаются наборы данных, называемые выборками. Для проведения их анализа данные подвергаются статистической обработке. Первое, что всегда делается при обработке данных, это вычисление элементарных статистических характеристик выборок (как минимум: среднего, среднеквадратичного отклонения, ошибки среднего) по каждому параметру и по каждой группе. Полезно также вычислить эти характеристики для объединения родственных групп и суммарно по всем данным.
Использование специальных функций
В мастере функций «MS Excel» имеется ряд специальных функций, предназначенных для вычисления выборочных характеристик. Прежде всего, это функции, характеризующие центр распределения.
-
Функция СРЗНАЧ вычисляет среднее арифметическое из нескольких массивов (аргументов) чисел. Аргументы число1, число2, ... − это от 1 до 30 массивов, для которых вычисляется среднее. Например, если ячейки А1:А7 содержат числа 10,14,5,6,10,12 и 13, то средним арифметическим СРЗНАЧ(А1:А7) является 10 (рис. 1.5.).
-
Функция СРГАРМ позволяет получить среднее гармоническое множества данных. Среднее гармоническое − это величина, обратная к среднему арифметическому обратных величин. Например, СРГАРМ( 10;14;5;6;10;12;13) равняется 8,317.
-
Функция СРГЕ0М вычисляет среднее геометрическое значений массива положительных чисел. Функцию СРГЕОМ можно использовать для вычисления средних показателей динамического ряда.
Например, СРГЕ0М(10;14;5;6;10;12;13) равняется 9,414.
-
Функция МЕДИАНА позволяет получать медиану заданной выборки. Медиана − это элемент выборки, число элементов выборки со значениями больше которого и меньше которого равно. Например, МЕДИАНА( 10;14; 5;6;10;12;13) равняется 10.
-
РИС. 1.5. Диалоговое окно функции СРЗНАЧ
-
Функция МОДА вычисляет наиболее часто встречающееся значение в выборке. Например, МОДА(10;14;5;6;10;12;13) равняется 10.
К специальным функциям, вычисляющим выборочные характеристики, характеризующие рассеяние вариант, относятся ДИСП, СТАНД0ТКЛ0Н, ПЕРСЕНТИЛЬ.
О Функция ДИСП позволяет оценить дисперсию по выборочным данным. Например, ДИСП(10;14;5;6;10;12;13) равняется 11,667.
О Функция СТАНДОТКЛОН вычисляет стандартное отклонение. Например, СТАНДОКЛОН(10;14;5;6;10;12;13) равняется 3,411.
О Функций ПЕРСЕНТШЬ позволяет получить квантили заданной выборки. Например, если ячейки А1:А7 содер-жат числа 10,14,5,6,10,12 и 13, то квантилю со значением 0,1 является ПЕРСЕНТИЛЬ(A1А7;0,1), равная 5,6
Форму эмпирического распределения позволяют оценить специальные функции ЭКСЦЕСС и СКОС.
О Функция ЭКСЦЕСС вычисляет оценку эксцесса по выборочным данным. Напри-, мер, ЭКСЦЕСС(10;14;5;6;10;12;13) равняется -1,169.
O Функция СКОС позволяет оценить асимметрию выборочного распределения.
Например, СКОС(10;14;5,-6;10;12:13) равняется -0,527.
Пример 1.3. Рассматриваются ежемесячные количества реализованных турфирмой путевок за периоды до и после начала активной рекламной компании. Ниже приведены количества реализованных путевок по месяцам.
С рекламой Без рекламы
162 135
156 126
144 115
137 140
125 121
145 112
151 130
Требуется найти средние значения и стандартные отклонения этих данных.
Решение
-
Для проведения статистического анализа прежде всего необходимо ввести данные в рабочую таблицу. Откройте новую рабочую таблицу. Введите в ячейку А1 слово Реклама, затем в ячейки А2:А8 − соответствующие значения числа реализованных путевок. В ячейку В1 введите слова Без рекламы, а в В2:В8 − значения числа реализованных путевок до начала рекламной компании. Отметим, что рассматриваемые группы данных со статистической точки зрения являются выборками.
-
При статистическом анализе прежде всего необходимо определить характеристики выборки, и важнейшей характеристикой является среднее значение. Для определения среднего значения в контрольной группе необходимо установить табличный курсор в свободную ячейку (А9). На панели инструментов нажмите кнопку Вставка функции (fx). В появившемся диалоговом окне Мастер функций выберите категорию Статистические и функцию СРЗНАЧ, после чего нажмите кнопку ОК. Появившееся диалоговое окно СРЗНАЧ за серое поле мышью отодвиньте вправо на 1-2 см отданных (при нажатой левой кнопке). Указателем мыши введите диапазон данных контрольной группы для определения среднего значения (А2:А8). Нажмите кнопку ОК. В ячейке А9 появится среднее значение выборки − 145,714.
В качестве упражнения определите в ячейке В9 среднее значение числа реализованных путевок без активной рекламы. Для этого табличный курсор установите в ячейку В9. На панели инструментов нажмите кнопку Вставка функции (fx). В появившемся диалоговом окне выберите категорию Статистические и функцию СРЗНАЧ , после чего нажмите кнопку ОК. Появившееся диалоговое окно СРЗНАЧ за серое поле мышью отодвиньте вправо на 1 -2 см от данных (при нажатой левой кнопке). Указателем мыши введите диапазон данных для определения среднего значения (В2:В8). Нажмите кнопку ОК. В ячейке В9 появится среднее значение выборки − 125,571.
3. Следующей
по важности характеристикой выборки
является мера разброса
элементов
выборки от среднего значения. Такой
мерой является среднее квадратичное
или стандартное отклонение. Для
определения стандартного отклонения
в контрольной группе необходимо
установить табличный курсор в свободную
ячейку
(А10). На панели инструментов нажмите
кнопку Вставка функции (fx).
В появившемся диалоговом окне Мастер
функций выберите категорию Статистические
и функцию СТАНДОТКЛОН, после чего
нажмите кнопку ОК. Появившееся
диалоговое окно СТАНДОТКЛОН за серое
поле мышью отодвиньте вправо на 1
-2 см от данных (при нажатой левой кнопке).
Указателем мыши введите диапазон данных
контрольной группы для определения
стандартного отклонения (А2.А8).
Нажмите
кнопку ОК. В ячейке А10 появится стандартное
отклонение выборки
− 12,298. Существует правило, согласно
которому при отсутствии артефактов
данные должны лежать в диапазоне М ±
З![]() (в примере 145,7±36,9).
(в примере 145,7±36,9).
В качестве упражнения требуется в ячейке В10 определить стандартное отклонение числа проданных путевок до начала рекламной компании. Для этого установите табличный курсор в ячейку В10. На панели инструментов нажмите кнопку Вставка функции (fx). В появившемся диалоговом окне выберите категорию Статистические и функцию СТАНДОТКЛОН, после чего нажмите кнопку ОК. Появившееся диалоговое окно СТАНДОТКЛОН за серое поле мышью отодвиньте вправо на 1−2см от данных (при нажатой левой кнопке). Указателем мыши введите диапазон данных для определения стандартного отклонения (В2:В8). Нажмите кнопку ОК. В ячейке В10 появится стандартное отклонение выборки − 10,277.
Упражнения
-
Найдите среднее значение и стандартное отклонение результатов бега на дистанцию 100 м у группы студентов: 12,8; 13,2; 13,0; 12,9; 13,5; 13,1.
-
Найдите выборочные среднее, медиану, моду, дисперсию и стандартное отклонение для следующей выборки 26,35,29,27,33,35,30,33,31,29.
-
Определите верхнюю (0,75) и нижнюю (0,25) квартили для выборки результатов измерений роста группы студенток: 164, 160, 157, 166, 162, 160, 161, 159, 160, 163, 170, 171.
-
Определите выборочные асимметрию и эксцесс для данных измерений роста из упражнения 1.
Использование инструментов Пакета анализа
В пакете «MS Excel» помимо мастера функций имеется набор более мощных инструментов для работы с несколькими выборками и углубленного анализа данных, называемый Пакет анализа, который может быть использован для решения задач статистической обработки выборочных данных.
Для установки раздела Анализ данных в пакете «MS Excel» сделайте следующее:
О в меню Сервис выберите команду «Надстройки»;
О в появившемся списке установите флажок «Пакет анализа».
Ввод данных. Исследуемые данные следует представить в виде таблицы, где столбцами являются соответствующие показатели. При создании таблицы «MS Excel» информация вводится в отдельные ячейки. Совокупность ячеек, содержащих анализируемые данные, называется входным диапазоном.
Последовательность обработки данных. Для использования статистического пакета анализа данных необходимо:
О указать курсором мыши на пункт меню «Сервис» и щелкнуть левой кнопкой мыши;
О в раскрывающемся списке выбрать команду «Анализ данных» (если команда Анализ данных отсутствует в меню «Сервис», то необходимо установить в «MS Excel» пакет анализа данных входя в «Сервис» → «Надстройки…» → «Пакет анализа» );
О выбрать необходимую строку в появившемся списке «Инструменты анализа»;
О ввести входной и выходной диапазоны и выбрать необходимые параметры.
Нахождение основных выборочных характеристик. Для определения характеристик выборки используется процедура Описательная статистика. Процедура позволяет получить статистический отчет, содержащий информацию о центральной тенденции и изменчивости входных данных. Для выполнения процедуры необходимо:
-
выполнить команду Сервис →Анализ данных;
-
в появившемся списке Инструменты анализа выбрать строку Описательная статистика и нажать кнопку ОК (рис. 1.6);
Рис. 1.6 Окно выбора метода обработки данных
-
в появившемся диалоговом окне указать входной диапазон, то есть ввести ссылку на ячейки, содержащие анализируемые данные. Для этого следует навести указатель мыши на левую верхнюю ячейку данных, нажать левую кнопку мыши и, не отпуская ее, протянуть указатель мыши к правой нижней ячейке, содержащей анализируемые данные, затем отпустить левую кнопку мыши;
-
указать выходной диапазон, то есть ввести ссылку на ячейки, в которые будут выведены результаты анализа. Для этого следует поставить переключатель в положение Выходной диапазон (навести указатель мыши и щелкнуть левой клавишей), далее навести указатель мыши в поле ввода Выходной диапазон и щелкнуть левой кнопкой мыши, затем указатель мыши навести на левую верхнюю ячейку выходного диапазона и щелкнуть левой кнопкой мыши;
-
в разделе «Группировка» переключатель установить в положение по столбцам;
-
установить флажок в поле «Итоговая статистика»;
-
нажать кнопку ОК.
В результате анализа в указанном выходном диапазоне для каждого столбца данных выводятся следующие статистические характеристики: среднее, стандартная ошибка (среднего), медиана, мода, стандартное отклонение, дисперсия выборки, эксцесс, асимметричность, интервал, минимум, максимум, сумма, счет, наибольшее; наименьшее, уровень надежности.
Пример 1.4. Рассматривается зарплата основных групп работников гостиницы: администрации, обслуживающего персонала и работников ресторана. Были получены следующие данные:
-
Администрация
Персонал
Ресторан
4500
2100
3200
4000
2100
3000
3700
2000
2500
3000
2000
2000
2500
2000
1900
1900
1800
1800
1800
Необходимо определить основные статистические характеристики в группах данных.
Решение
-
Для использования инструментов анализа исследуемые данные следует представить в виде таблицы, где столбцами являются соответствующие показатели. Значения зарплат сотрудников администрации введите в диапазон А1:А5, обслуживающего персонала − в диапазон В1:В8 и т. д. В результате получится таблица, представленная на рис. 1.7.
-
А
В
С
1
4500
2100
3200
2
4000
2100
3000
3
3700
2000
2500
4
3000
2000
2000
5
2500
2000
1900
6
1900
1800
7
1800
8
1800
Рис. 1.7. Таблица из примера 1.4
Далее необходимо провести элементарную статистическую обработку. Для этого, указав курсором мыши на пункт меню Сервис, выберите команду Анализ данных. Затем в появившемся списке Инструменты анализа выберите строку Описательная статистика.
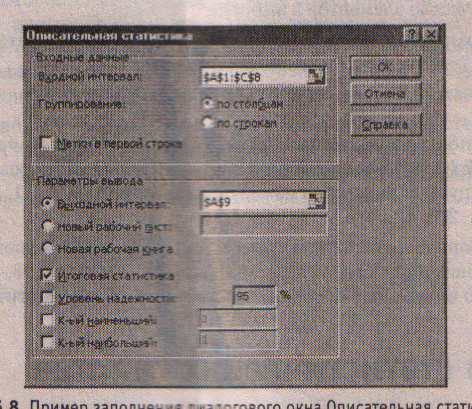
Рис. 1.8. Пример заполнения диалогового окна Описательная статистика
3. В появившемся диалоговом окне (рис. 1.8) в рабочем поле Входной интервал укажите входной диапазон — А 1:С8. Активировав переключателем рабочее поле Выходной интервал, укажите выходной диапазон − ячейку А9. В разделе Группировка переключатель установите в положение по столбцам. Установите флажок в поле Итоговая статистика и нажмите кнопку ОК.