Файл: Пособие Экселя.doc

В результате анализа (рис. 1.9) в указанном выходном диапазоне для каждого стол­бца данных получим соответствующие результаты.

Рис. 1.9. Результаты работы инструмента «Описательная статистика»

Все полученные характеристики были рассмотрены ранее в разделе «Выборочные характеристики» данной главы, за исключением последних четырех:

О минимум − значение минимального элемента выборки;

О максимум − значение максимального элемента выборки;

О сумма − сумма значений всех элементов выборки;

О счет − количество элементов в выборке.

Среди этих характеристик наиболее важными являются показатели Среднее, Стан­дартная ошибка (среднего) и Стандартное отклонение.

Упражнения

8. Найдите наиболее популярный туристический маршрут из четырех реализуе­мых фирмой (моду), если за неделю последовательно были реализованы следу­ющие маршруты (приводятся номера маршрутов); 1,3,3,2,1, 1,1, 4,4,2,4,1,3,2, 4,1,4,4,3,1,2,3,4,1,1,3.

9. В рабочей зоне производились замеры концентрации вредного вещества. По­лучен ряд значений (в мг/м³): 12, 16, 15, 14, 10,20,16, 14, 18, 14, 15, 17, 23, 11. Необходимо определить основные выборочные характеристики.

Проверка статистических гипотез

Помимо описательной статистики, важной областью является также аналитиче­ская статистика. Как уже указывалось в разделе «Понятие математической стати­стики», аналитическая статистика или теория статистических выводов ориенти­рована на обработку данных, полученных в ходе эксперимента, с целью формули­ровки выводов, имеющих прикладное значение. Здесь решается вопрос, отражают ли наблюдаемые данные объективно существующую реальность. Указанный вопрос решается проверкой соответствующих статистических гипотез. При этом мо­гут выявляться достоверности различий между выборками, взаимосвязи между выборками, влияющие факторы и т. п.

Принятие статистических решений

Статистическая гипотеза − это предположение о виде или отдельных параметрах распределения вероятностей, которое подлежит проверке на имеющихся данных.

Проверка статистических гипотез − это процесс формирования решения о возмож­ности принять или отвергнуть утверждение (гипотезу), основанный на информации, полученной из анализа выборки. Методы проверки гипотез называются критериями.

В большинстве случаев рассматривают так называемую нулевую гипотезу (нуль-гипотезу Н₀), состоящую в том, что все события произошли случайно, естествен­ным образом. Альтернативная гипотеза (H₁) состоит в том, что события случай­ным образом произойти не могли, и имело место воздействие некого фактора.

Обычно нулевая гипотеза формулируется таким образом, чтобы на основании эк­сперимента или наблюдений ее можно было отвергнуть с заранее заданной веро­ятностью ошибки а. Эта, заранее заданная вероятность ошибки, называется уров­нем значимости.

Уровень значимости − максимальное значение вероятности появления события, при котором событие считается практически невозможным. В статистике наиболь­шее распространение получил уровень значимости, равный = 0,05. Поэтому если вероятность, с которой интересующее событие может произойти случайным обра­зом р < 0,05, то принято считать это событие маловероятным, и если оно все же произошло, то это не было случайным. В наиболее ответственных случаях, когда требуется особая уверенность в достоверности полученных результатов, надежно­сти выводов, уровень значимости принимают равным а = 0,01 или даже а = 0,001.

Величину Р, равную 1 - , называют доверительной вероятностью (уровнем на­дежности), то есть вероятностью, признанной достаточной для того, чтобы уве­ренно судить о принятом статистическом решении. Соответственно, в качестве до­верительных вероятностей выбирают значения 0,95,0,99 и 0,999.

Доверительный интервал

Распределение Границы интервала

M-2m M M+2m

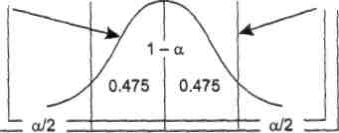
Рис. 1.10. 95%-ный доверительный интервал для среднего значения

Интервал, в котором с заданной доверительной вероятностью Р = 1 - находится оцениваемый параметр, называется доверительным интервалом. В соответствии с доверительными вероятностями на практике используются 95%-, 99%-, 99,9%-ные доверительные интервалы. Граничные точки доверительного интервала называют доверительными пределами (рис. 1.10).

Выбор того или иного уровня значимости, выше которого результаты отвергаются как статистически не подтвержденные, или, соответственно, доверительной веро­ятности, в общем случае является произвольным. Окончательное решение зави­сит от исследователя, традиций и накопленного практического опыта в данной области исследований.

Анализ одной выборки

Анализ однородности выборки. Одним из важных вопросов, возникающих при анализе выборки, является вопрос: относится та или иная варианта к данной ста­тистической совокупности? Решение вопроса не представляет сложности, если распределение в этой совокупности является нормальным. Для этого достаточно использовать правило трех сигм. Согласно этому правилу, в пределах М ± З на­ходится 99,7% всех вариант. Поэтому, если варианта попадает в этот интервал, то она считается принадлежащей к данной совокупности. Если не попадает, то она может быть отброшена. Хотя этот метод и предполагает нормальность исходного распределения, на практике он успешно работает и может быть использован в боль­шинстве других случаев.

При числе элементов в выборке п < 30 способ более точного определения границ доверительного интервала по формуле

[M-t_n,p s; M + t_n,p s] _(1.1)

будет показан ниже в примере 1.5. В формуле (1.1) М − среднее значение, s − стан­дартное отклонение, t_n,p − табличное значение распределения Стьюдента с числом степеней свободы п и доверительной вероятностью р.

Построение доверительных интервалов для среднего. Еще одной важной зада­чей, возникающей при анализе одной выборки, является сравнение выборочного среднего арифметического со средним значением генеральной совокупности. Эта задача решается с помощью статистических критериев. При этом выясняется, зна­чимо ли отличие выборочного среднего значения от среднего значения генераль­ной совокупности, из которой предположительно взята выборка, или наблюдае­мое различие является случайным.

Действительно, средние значения, получаемые по выборочным данным, обычно не совпадают с генеральным средним (математическим ожиданием). В связи с этим возникает вопрос: можно ли по результатам выборочной оценки судить о свой­ствах всей генеральной совокупности?

Поскольку каждую оценку, полученную в отдельной выборке, можно рассматри­вать как случайную величину, то при увеличении числа выборок распределение отдельных оценок будет принимать характер нормального распределения. Это зна­чит, что в случае средних арифметических значения выборочных средних относи­тельно генерального среднего распределяются по нормальному закону. То есть так же, как относительные отклонения нормально распределенных вариант от средне­го арифметического выборки.

Отсюда, в частности, следует, что 68,3% всех выборочных средних находятся в пре­делах = М ±т, где − предельная ошибка выборки, М − среднее выборочное, т − стандартная ошибка среднего значения. Иными словами, имеется вероят­ность 0,683, что выборочное среднее отличается от генерального не более, чем на ±т. Здесь 0,683 − доверительная вероятность, 1 - 0,683 = 0,317 − уровень значи­мости а, = М ± т − 68% доверительный интервал.

Для принятой в большинстве исследований доверительной вероятности 0,95, до­верительный интервал для средних при достаточно большом числе наблюдений (n > 30) примерно равен ±2т (см. рис. 1.8). При доверительной вероятности 0,99, доверительный интервал составит примерно ±3т. Для более точного определения границ доверительного интервала можно воспользоваться формулой

[M-t_n,p; M + t_n,p]

где М − среднее значение, s − стандартное отклонение, t_n,p − табличное значение распределения Стьюдента с числом степеней свободы n и доверительной вероят­ностью р, n− количество элементов в выборке.

В MS «MS Excel» для более точного вычисления границ доверительного интервала и при числе элементов в выборке п < 30 можно воспользоваться функцией ДОВЕРИТ или процедурой Описательная статистика.

Функция ДОВЕРИТ(алъфа; станд-откл;размер) определяет полуширину довери­тельного интервала и содержит следующие параметры:

О Альфа − уровень значимости, используемый для вычисления доверительной вероятности. Доверительная вероятность равняется 100*(1 - альфа)% процен­там, или, другими словами, альфа, равное 0,05, означает 95%-ный уровень дове­рительной вероятности;

О Станд-откл − стандартное отклонение генеральной совокупности для интер­вала данных, предполагается известным;

О Размер − это размер выборки.

Пример 1.5. Найти границы 95%-ного доверительного интервала для среднего зна­чения, если у 25 телефонных аккумуляторов среднее время разряда в режиме ожи­дания составило 140 часов, а стандартное отклонение − 2,5 часа.

Решение

1. Откройте новую рабочую таблицу. Установите табличный курсор в ячейку А1.

2. Для определения границ доверительного интервала необходимо на панели ин­струментов Стандартная нажать кнопку Вставка функции (fx). В появившемся диалоговом окне Мастер функций выберите категорию Статистические и функцию ДОВЕРИТ, после чего нажмите кнопку ОК.

3. В рабочие поля появившегося диалогового окна ДОВЕРИТ с клавиатуры введите условия задачи; Альфа − 0,05; Станд-откл −2,5; Размер −25 (рис. 1.11). Нажми­те кнопку ОК.

4. В ячейке А1 появится полуширина 95%-ного доверительного интервала для среднего значения выборки — 0,979981. Другими словами, с 95%-ным уровнем надежности можно утверждать, что средняя продолжительность разряда акку­мулятора составляет 140 ± 0,979981 часа или от 139,02 до 140,98 часа.

Рис. 1.1. Пример заполнения диалогового окна «ДОВЕРИТ»

Пример 1.1. Пусть имеется выборка, содержащая числовые значения: 13, 15, 17, 19,22,25,19. Необходимо определить границы 95%-ного доверительного интерва­ла для среднего значения и для нахождения «выскакивающей» варианты.

Решение

1. В диапазон А1:А7 введите исходный ряд чисел.

2. Далее вызовите процедуру Описательная статистика. Для этого, указав курсором мыши на пункт меню Сервис, выберите команду Анализ данных. Затем в появив­шемся списке Инструменты анализа выберите строку Описательная статистика.

3. В появившемся диалоговом окне в рабочем поле Входной интервал: укажите вход­ной диапазон − А 1:А7. Переключателем активизируйте Выходной интервал и ука­жите выходной диапазон — ячейку В1. В разделе Группировка переключатель установите в положение по столбцам. Установите флажок в левое поле Уровень надежности: и в правом поле (%) −95. Затем нажмите кнопку ОК.

4. В результате анализа в указанном выходном диапазоне для доверительной ве­роятности 0,95 получаем значения доверительного интервала (рис. 1.12).

Рис. 1.12. Исходная выборка (А1:А7) и результат вычислений (СЗ) из примера 1.6

Уровень надежности − это половина доверительного интервала для генерального среднего арифметического. Из полученного результата следует, что с вероятнос­тью 0,95 среднее арифметическое для генеральной совокупности находится в интервале 18,571 ± 3,77. Здесь 18,571 − выборочное среднее М для рассматриваемо­го примера, которое находится обычно процедурой Описательная статистика одно­временно с доверительным интервалом.

5. Для нахождения доверительных границ для «выскакивающей» варианты необ­ходимо полученный выше доверительный интервал умножить на (в приме­ре , то есть 3,77* =9,975). В «MS Excel» это можно выполнить следующим образом. Табличный курсор установите в свободную ячейку С4; введите с клави­атуры знак =; мышью укажите на ячейку СЗ (в которой находится результат вы­числений); введите с клавиатуры знак *; с панели инструментов Стандартная вы­зовите Мастер функций (кнопка fx); выберите категорию Математические, тип функции Корень; нажмите ОК; введите с клавиатуры число 7 и нажмите ОК. В результате получим в ячейке С4 значение доверительного интервала − 9,975.

Таким образом, варианта, попадающая в интервал 18,571 ± 9,975, считается при­надлежащей данной совокупности с вероятностью 0,95. Выходящая за эти грани­цы может быть отброшена с уровнем значимости = 0,05.

Проверка соответствия теоретическому распределению. Следующей задачей, воз­никающей при анализе одной выборки, является оценка меры соответствия (рас­хождения) полученных эмпирических данных и каких-либо теоретических рас­пределений. Это связано с тем, что в большинстве случаев при решении реальных задач закон распределения и его параметры неизвестны. В то же время применяе­мые статистические методы в качестве предпосылок часто требуют определенного закона распределения.

Наиболее часто проверяется предположение о нормальном распределении генераль­ной совокупности, поскольку большинство статистических процедур ориентировано на выборки, полученные из нормально распределенной генеральной совокупности.

Для оценки соответствия имеющихся экспериментальных данных нормальному закону распределения обычно используют графический метод, выборочные пара­метры формы распределения и критерии согласия.

Графический метод позволяет давать ориентировочную оценку расхождения или совпадений распределений (рис. 1.13).

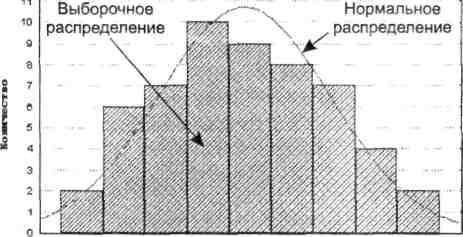
56 57 58 59 60 61 62 63 64 65

Вес

Рис. 1.13. Сопоставление выборочного распределения веса студенток и кривой нормального распределения

При большом числе наблюдений (n > 100) неплохие результаты дает вычисление выборочных параметров формы распределения: эксцесса и асимметрии (см. раз­делы «Использование специальных функций» и «Использование инструментов Пакета анализа»). Принято говорить, что предположение о нормальности распре­деления не противоречит имеющимся данным, если асимметрия близка к нулю, то есть лежит в диапазоне от -0,2 до 0,2, а эксцесс − от 2 до 4.

Наиболее убедительные результаты дает использование критериев согласия. Кри­териями согласия называют статистические критерии, предназначенные для про­верки согласия опытных данных и теоретической модели. Здесь нулевая гипотеза Н₀ представляет собой утверждение о том, что распределение генеральной сово­купности, из которой получена выборка, не отличается от нормального. Среди кри­териев согласия большое распространение получил непараметрический критерий (хи-квадрат). Он основан на сравнении эмпирических частот интервалов груп­пировки с теоретическими (ожидаемыми) частотами, рассчитанными по форму­лам нормального распределения.

Отметим, что сколько-нибудь уверенно о нормальности закона распределения можно судить, если имеется не менее 50 результатов наблюдений. В случаях мень­шего числа данных можно говорить только о том, что данные не противоречат нор­мальному закону, и в этом случае обычно используют графические методы оценки соответствия. При большем числе наблюдений целесообразно совместное исполь­зование графических и статистических (например, тест хи-квадрат или аналогич­ные) методов оценки, естественно дополняющих друг друга.

Использование критерия согласия хи-квадрат. Для применения критерия жела­тельно, чтобы объем выборки п > 40, выборочные данные были сгруппированы в интервальный ряд с числом интервалов не менее 7, а в каждом интервале находи­лось не менее 5 наблюдений (частот).

Отметим, что сравниваться должны именно абсолютные частоты, а не относитель­ные (частоты). При этом, как и любой другой статистический критерий, крите­рий хи-квадрат не доказывает справедливость нулевой гипотезы (соответствие эмпирического распределения нормальному), а лишь может позволить ее отверг­нуть с определенной вероятностью (уровнем значимости).

В MS «MS Excel» критерий хи-квадрат реализован в функции ХИ2ТЕСТ. Функция ХИ2-ТЕСТ вычисляет вероятность совпадения наблюдаемых (фактических) значений и теоретических (гипотетических) значений. Если вычисленная вероятность ниже уровня значимости (0,05), то нулевая гипотеза отвергается и утверждается, что наблюдаемые значения не соответствуют нормальному закону распределения. Если вычисленная вероятность близка к 1, то можно говорить о высокой степени соот­ветствия экспериментальных данных нормальному закону распределения.

Функция имеет следующие параметры:

ХИ2ТЕСТ (фактический_интервал;ожидаемый_интервал). Здесь:

О фактический_интервал − это интервал данных, которые содержат наблюдения, подлежащие сравнению с ожидаемыми значениями;

О ожидаемый интервал − это интервал данных, который содержит теоретические (ожидаемые) значения для соответствующих наблюдаемых.

Пример 1.7. Проверить соответствие выборочных данных из примера 1.1. (64, 57, 63,62,58, 61, 63, 60, 60,61,65,62, 62, 60, 64, 61,59,59, 63,61, 62,58, 58, 63, 61, 59, 62, 60,60,58,61,60,63,63,58,60,59,60,59,61,62,62,63,57,61,58,60,64,60,59,61,64, 62, 59, 65) нормальному закону распределения.

Решение

1. Повторите пункты 1-7 решения примера 1.1. В результате получится таблица (см. рис. 1.2).

2. Найдите теоретические частоты нормального распределения. Для этого пред­варительно необходимо найти среднее значение и стандартное отклонение вы­борки.

В ячейке I13 с помощью функции СРЗНАЧ найдите среднее значение для данных из диапазона А2:Е12 (60,855). В ячейке J1З с помощью функции СТАНД0ТКЛ0Н най­дите стандартное отклонение для этих же данных (2,05). В ячейки К1 и К2 введите название столбца − Теоретические частости. Затем с помощью функции НОРМ-РАСП найдите теоретические частости. Установите курсор в ячейку К4, вызовите указанную функцию и заполните ее рабочие поля: х − G4; Среднее − $1$13; Стан-дартное_откл − $J$13; Интегральный − 0. Получим в ячейке К4 0,033. Далее протя­гиванием скопируйте содержимое ячейки К4 в диапазон ячеек К5:К12. Затем в ячей­ки L1 и L2 введите название нового столбца − Теоретические частоты. Установите курсор в ячейку L4 и введите формулу =Н$13*К4. Далее протягиванием скопи­руйте содержимое ячейки L4 в диапазон ячеек L5:L12. Результаты вычислений представлены на рис. 1.14.

G	H	I	J	K	L
Вес кг	Абсолютные частоты	Относи- тельные частоты	Накопленные частоты	Теоретические частости	Теоретические частоты
57	2	0,036364	0,036364	0,033205828	1,82632055
58	6	0,109091	0,145454909	0,073795567	4,058756212
59	7	0,127273	0,272727636	0,129258576	7,109221655
60	10	0,181818	0,454545818	0,178443849	9,814411704
61	9	0,163636	0,618182182	0,194158732	10,67873029
62	8	0,145455	0,763636727	0,16650428	9,157735407
63	7	0,127273	0,890909455	0,112540024	6,189701326
64	4	0,072727	0,963636727	0,059951732	3,297345259
65	2	0,036364	1,000000364	0,025171529	1,384434082

Рис. 1.14. Результаты вычисления теоретических частостей и частот из примера 1.7

С помощью функции ХИ2ТЕСТ определите соответствие данных нормальному закону распределения. Для этого установите табличный курсор в свободную ячейку L13. На панели инструментов Стандартная нажмите кнопку Вставка функ­ции (f_x). В появившемся диалоговом окне Мастер функций выберите категорию Статистические и функцию ХИ2ТЕСТ, после чего нажмите кнопку ОК. Появившее­ся диалоговое окно ХИ2ТЕСТ отодвиньте вправо на 1-2 см от данных. Указате­лем мыши в рабочие поля введите фактический Н4:Н12 и ожидаемые L4:L12 ди­апазоны частот (рис. 1.15). Нажмите кнопку ОК. В ячейке L13 появится значение вероятности того, что выборочные данные соответствуют нормальному закону распределения − 0,9842.

Рис. 1.15. Пример заполнения рабочих полей функции ХИ2ТЕСТ

4. Поскольку полученная вероятность соответствия экспериментальных данных р = 0,98 много больше, чем уровень значимости = 0,05, то можно утверждать, что нулевая гипотеза не может быть отвергнута и, следовательно, данные не противоречат нормальному закону распределения. Более того, поскольку по­лученная вероятность р = 0,98 близка к 1, можно говорить о высокой степени вероятности того, что экспериментальные данные соответствуют нормально­му закону.

Упражнения

10. Определите, лежит ли значение 19 внутри границ 95%-ного доверительного интервала выборки 2, 3, 5, 7, 4, 9, 6,4, 9,10,4, 7, 19.

11. Определите с уровнем значимости 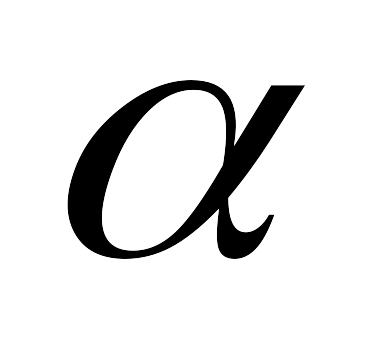= 0,05 максимальное отклонение средне­го значения генеральной совокупности от среднего выборки 3, 4, 4, 2, 5, 3, 4, 3, 5, 4, 3, 5, 1.

12. Найдите соответствие экспериментальных данных нормальному закону рас­пределения для следующей выборки весов детей (кг): 21, 21, 22, 22, 22, 22, 22, 22, 22, 22, 22, 23, 23, 23, 23, 23, 23, 24, 24, 24, 24, 24, 24, 24, 24, 24, 24, 24, 25, 25, 25, 25, 25, 25, 25, 25, 25, 25, 25, 25, 25, 25, 25, 25, 25, 21, 21, 21, 21, 21, 21, 21, 21, 21, 26, 26, 26, 26, 26, 27, 27.

Анализ двух выборок

Выявление достоверности различий. Следующей задачей статистического ана­лиза, решаемой после определения основных выборочных характеристик и ана­лиза одной выборки, является совместный анализ нескольких выборок. Важ­нейшим вопросом, возникающим при анализе двух выборок, является вопрос о наличии различий между этими выборками. Обычно для этого проводят провер­ку статистических гипотез о принадлежности обеих выборок одной генеральной совокупности или о равенстве генеральных средних. В рассмотренном ранее при­мере 1.3. такие различия выявляются путем сравнения данных реализации тур­фирмой путевок за периоды до и после начала активной рекламной компании. Если сопоставить средние значения числа реализованных за месяц путевок до (125,6) и после (145,7) начала рекламной компании, видно, что они различают­ся. Можно ли по этим данным сделать вывод об эффективности рекламной ком­пании?

Для решения задач такого типа используются так называемые критерии различия. Для проверки одной и той же гипотезы могут быть использованы разные статис­тические критерии. Правильный выбор критерия определяется как спецификой данных и проверяемых гипотез, так и уровнем статистической подготовки иссле­дователя.

Статистические критерии различия подразделяются на параметрические и непа­раметрические критерии. Параметрические критерии служат для проверки гипо­тез о параметрах определенных распределений генеральной совокупности (чаще всего нормального распределения). Непараметрические критерии для проверки гипотез не используют предположений о законе распределения генеральной сово­купности и не требуют знания параметров распределения.

Параметрические критерии. Параметрические критерии служат для проверки гипотез о положении и рассеивании. Из параметрических критериев наибольшей популярностью при проверке гипотез о равенстве генеральных средних (матема­тических ожиданий) пользуется f-критерий Стьюдента (t-критерий различия).

Критерий Стьюдента (t) наиболее часто используется для проверки гипотезы: «Средние двух выборок относятся к одной и той же совокупности». Критерий по­зволяет найти вероятность того, что оба средних относятся к одной и той же сово­купности. Если эта вероятность р ниже уровня значимости (р < 0,05), то принято считать, что выборки относятся к двум разным совокупностям.

При использовании t-критерия можно выделить два случая. В первом случае его применяют для проверки гипотезы о равенстве генеральных средних двух неза­висимых, несвязанных выборок (так называемый двухвыборочный t-критерий). В этом случае есть контрольная группа и опытная группа, состоящие, например, из разных пациентов, количество которых в группах может быть различно.

Во втором случае, когда одна и та же группа объектов порождает числовой матери­ал для проверки гипотез о средних, используется так называемый парный t-критерий. Выборки при этом называют зависимыми, связанными. Например, измеряет­ся содержание лейкоцитов у здоровых животных, а затем у тех же самых животных после облучения определенной дозой излучения.

В обоих случаях в принципе должно выполняться требование нормальности рас­пределения исследуемого признака в каждой из сравниваемых групп и равенства дисперсий в сравниваемых совокупностях. Однако на практике по большому сче­ту корректное применение t-критерия Стьюдента для двух групп часто бывает за­труднительно, поскольку достоверно проверить эти условия удается далеко не всегда.

Для оценки достоверности отличий по критерию Стьюдента принимается нуле­вая гипотеза, что средние выборок равны между собой. Затем вычисляется значе­ние вероятности того, что изучаемые события (например, количества реализован­ных путевок в обеих выборках) произошли случайным образом.

В MS «MS Excel» для оценки достоверности отличий по критерию Стьюдента использу­ются специальная функция «ТТЕСТ» и процедуры пакета анализа (см. раздел «Ис­пользование Пакета анализа для выявления различий» ниже).

Все перечисленные инструменты вычисляют вероятность, соответствующую кри­терию Стьюдента, и используются, чтобы определить, насколько вероятно, что две выборки взяты из генеральных совокупностей, которые имеют одно и то же сред­нее.

Функция «ТТЕСТ» использует следующие параметры: ТТЕСТ (массив1; массив2; хвосты; -тип). Здесь:

О массив 1 − это первое множество данных;

О массш2 − это второе множество данных;

О хвосты − число хвостов распределения. Обычно число хвостов равно 2;

О тип − это вид исполняемого t-теста. Возможны 3 варианта выбора: 1 − пар­ный тест, 2 − двухвыборочный тест с равными дисперсиями, 3 − двухвыборочный тест с неравными дисперсиями.

Пример 1.8. Выявить, достоверны ли отличия при сравнении данных реализации турфирмой путевок за периоды до и после начала активной рекламной компании (см. пример 1.3).

Решение

1. Введите данные (как в пункте 1 примера 1.3).

1. Для выявления достоверности отличий табличный курсор установите в сво­бодную ячейку (А11). На панели инструментов необходимо нажать кнопку Встав­ка функции (f_х). В появившемся диалоговом окне Мастер функций выберите кате­горию Статистические и функцию ТТЕСТ, после чего нажмите кнопку ОК. Появившееся диалоговое окно ТТЕСТ за серое поле мышью отодвиньте вправо на 1-2 см от данных (при нажатой левой кнопке). Указателем мыши введите диапазон данных контрольной группы в поле Массив 1 (А2:А8). В поле Массив 2 введите диапазон данных исследуемой группы (В2:В8). В поле Хвосты всегда вводится с клавиатуры цифра 2 (без кавычек), а в поле Тип с клавиатуры введи­те цифру 3. Нажмите кнопку ОК. В ячейке А11 появится значение вероятнос­ти - 0,006295.

2. Поскольку величина вероятности случайного появления анализируемых вы­борок (0,006295) меньше уровня значимости ( 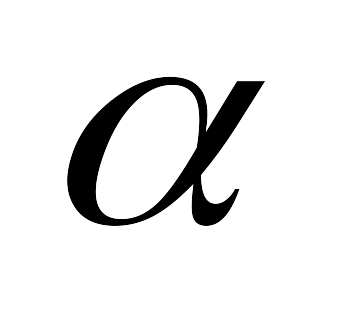= 0,05), то нулевая гипотеза отвергается. Следовательно, различия между выборками не случайные и сред­ние выборок считаются достоверно отличающимися друг от друга. Поэтому на основании применения критерия Стьюдента можно сделать вывод о боль­шей эффективности реализации путевок после начала рекламной компании (р < 0,05).

Как указывалось выше, при использовании t-критерия выделяют два основных случая. В первом случае его применяют для проверки гипотезы о равенстве гене­ральных средних двух независимых, несвязанных выборок (так называемый двух­выборочный t-критерий). В этом случае есть две различных выборки, количество элементов в которых может быть также различно. При заполнении диалогового окна ТТЕСТ при этом указывается Тип 3.

Во втором случае, когда одна и та же группа объектов порождает числовой матери­ал для проверки гипотез о средних, используется так называемый парный t-критерий. Выборки при этом называют зависимыми, связанными (при заполнении диалогового окна ТТЕСТ указывается Тип 1). Например, сравнивается реализация путевок двумя фирмами в соответствующие месяцы. В качестве упражнения рассмотрим пример.

Пример 1.9. Сравнивается количество наличных денег у двух групп студентов (в рублях);

А	В
30	10
30	20
40	30
50	40
60	50

Необходимо определить достоверность различия между группами при двух вари­антах постановки задачи:

О группы состоят из различных студентов (тип 3);

О группы состоят из одних и тех же студентов, но первая − до посещения буфета, а вторая − после (тип 1).

Решение. В ячейки С1:С5 введите количество денег у студентов первой группы. В ячейки D1:D5 введите количество денег у студентов второй группы,

1. Табличный курсор установите в свободную ячейку (С6). На панели инстру­ментов необходимо нажать кнопку Вставка функции (f_x). В появившемся диа­логовом окне Мастер функций выберите категорию Статистические и функцию ТТЕСТ, после чего нажмите кнопку ОК. Появившееся диалоговое окно ТТЕСТ за
серое поле мышью отодвиньте вправо на 1-2 см от данных (при нажатой левой кнопке). Указателем мыши ввести диапазон данных первой группы в поле Массив 1 (С1:С5). В поле Массив 2 введите диапазон данных второй группы (D1:D5). В поле Хвосты всегда вводится цифра 2 (без кавычек), а в поле Тип введите цифру 3. Нажмите кнопку ОК. В ячейке С6 появится значение вероят­ности - 0,228053.

Поскольку величина вероятности случайного появления анализируемых вы­борок (0,228053) больше уровня значимости ( = 0,05), то нулевая гипотеза не может быть отвергнута (принимается). Следовательно, различия между выбор­ками могут быть случайными и средние выборок не считаются достоверно от­личающимися друг от друга. Поэтому на основании применения критерия Стьюдента нельзя сделать вывод о достоверности отличий двух групп студентов по количеству карманных денег, имеющихся у них (р > 0,05).

3. Табличный курсор установите в свободную ячейку (D6). На панели инстру­ментов нажмите кнопку Вставка функции (f_x). В появившемся диалоговом окне Мастер функций выберите категорию Статистические и функцию ТТЕСТ, после чего нажмите кнопку ОК. Появившееся диалоговое окно ТТЕСТ за серое поле
   мышью отодвиньте вправо на 1-2 см от данных (при нажатой левой кноп­ке). Указателем мыши введите диапазон данных первой группы в поле Массив 1 (С1:С5). В поле Массив 2 введите диапазон данных второй группы (D1:D5).В поле Хвосты всегда вводится цифра 2 (без кавычек), а в поле Тип введите
   цифру 1. Нажмите кнопку ОК. В ячейке D6 появится значение вероятности −0,003883.

Поскольку величина вероятности случайного появления анализируемых выборок (0,003883) меньше уровня значимости ( = 0,05), то нулевая гипотеза отвергается. Следовательно, различия между выборками не могут быть случайными и средние выборок считаются достоверно отличающимися друг от друга. Поэтому на основании применения критерия Стьюдента можно сделать вывод о том, что в двух группах студентов выявлены достоверные отличия по количеству карманных де­нег (р < 0,05), что явилось результатом посещения буфета.

Таким образом, ясно, что применение различных типов критерия Стьюдента мо­жет приводить к различным результатам на основании одних и тех же исходных данных. Можно предложить следующий приблизительный способ выбора типа критерия: если не ясно, какой тип критерия выбирать, выбирается тип 3; если оче­видно, что выборки зависимы, связаны (например, это одни и те же студенты), то следует выбирать тип 1.

Критерий Фишера. Критерий Фишера используют для проверки гипотезы о при­надлежности двух дисперсий одной генеральной совокупности и, следовательно, их равенстве. При этом предполагается, что данные независимы и распределены по нормальному закону. Гипотеза о равенстве дисперсий принимается, если отно­шение большей дисперсии к меньшей меньше критического значения распределе­ния Фишера.

F=s₁²/s₂², F<F_крит

где Fкрит зависит от уровня значимости и числа степеней свободы для дисперсий в числителе и знаменателе.

В MS «MS Excel» для расчета уровня вероятности выполнения гипотезы о равенстве дисперсий могут быть использованы функция ФТЕСТ(массив1; массив2) и процеду­ра пакета анализа Двухвыборочный F-тест для дисперсий.

Непараметрические критерии. Непараметрические критерии используются в тех случаях, когда закон распределения данных отличается от нормального или неиз­вестен. Из большого числа непараметрических критериев рассмотрим критерий хи-квадрат.

Критерий согласия - Бывают ситуации, когда необходимо сравнить две относи­тельные или выраженные в процентах величины (доли). Примером может слу­жить случай проверки успешности трудоустройства молодых специалистов, когда известен процент трудоустроившихся выпускников двух институтов. Для провер­ки достоверности различий здесь критерий Стьюдента применить не удастся. В та­ких задачах обычно используют критерий (хи-квадрат). Критерий хи-квадрат относится к непараметрическим критериям.

Здесь, как и в случае с критерием Стьюдента, принимается нулевая гипотеза о том, что выборки принадлежат к одной генеральной совокупности. Кроме того, опреде­ляется ожидаемое значение результата. Обычно это среднее значение между вы­борками рассматриваемого показателя. Затем оценивается вероятность того, что ожидаемые значения и наблюдаемые принадлежат к одной генеральной совокуп­ности.

В MS «MS Excel» критерий хи-квадрат реализован в функции ХИ2ТЕСТ. Функция ХИ2-ТЕСТ вычисляет вероятность совпадения наблюдаемых (фактических) значений и теоретических (гипотетических) значений. Если вычисленная вероятность ниже уровня значимости (0,05), то нулевая гипотеза отвергается и утверждается, что наблюдаемые значения не соответствуют теоретическим (ожидаемым) значениям.

Функция имеет следующие параметры: ХИ2ТЕСТ(фактический_интервал; ожидаемый_интервал). Здесь:

О фактический^интервал − это интервал данных, которые содержат наблюде­ния, подлежащие сравнению с ожидаемыми значениями;

О ожидаемый_интервал − это интервал данных, который содержит теоретиче­ские (ожидаемые) значения для соответствующих наблюдаемых.

Пример 1.10. Пусть после окончания двух институтов экономического профиля трудоустроилось по специальности из первого института 90 человек, а из второго 60 (обе группы молодых специалистов включали по 100 человек).

Решение

1. Принимается нулевая гипотеза, что выборки принадлежат к одной генераль­ной совокупности.

2. Определяется ожидаемое значение результата (среднее значение между вы­борками): (60 + 90)/2 = 75, то есть мы ожидали, что разницы между группами нет, и в обоих случаях должно было трудоустроиться по 75 человек.

3. Затем вычисляется значение вероятности того, что изучаемые события (тру­доустройство в обеих выборках) произошли случайным образом. Для этого введите данные в рабочую таблицу: 90 − в ячейку Е1, 60 − в F1, 75 − в E2,F2. Табличный курсор установите в свободную ячейку (ЕЗ). На панели инстру­ментов нажмите кнопку Вставка функции (f_x). В появившемся диалоговом окне Мастер функций выберите категорию Статистические и функцию ХИ2ТЕСТ, после чего нажмите кнопку ОК. Появившееся диалоговое окно ХИ2ТЕСТ за серое поле мышью отодвиньте вправо на 1-2 см от данных (при нажатой левой кнопке). Указателем мыши введите диапазон данных наблюдавшегося количества тру­доустроившихся в поле Фактический интервал (E1:F1). В поле Ожидаемый интер­вал введите диапазон данных предполагаемого количества трудоустроивших­ся (E2:F2). Нажмите кнопку ОК. В ячейке ЕЗ появится значение вероятности − 0,014301.

4. Поскольку величина вероятности случайного появления анализируемых вы­борок (0,0143) меньше уровня значимости (а = 0,05), то нулевая гипотеза от­вергается. Следовательно, различия между выборками не могут быть случай­ными и выборки считаются достоверно отличающимися друг от друга. Поэтому на основании применения критерия хи-квадрат можно сделать вывод о том, что в двух группах выпускников выявлены достоверные отличия по успешно­сти трудоустройства (р < 0,05), что, по-видимому, явилось результатом более высокой репутации выпускников первого института.

Упражнения

13. Даны результаты бега на дистанции 100 м в секундах в двух группах студен­тов. Студенты первой группы в течение года посещали факультативные заня­тия по физкультуре. Определите, достоверны ли отличия по результатам бега в этих группах.

Посещавшие факультатив	Не посещавшие
12,3	13,2
11,9	13,0
12,2	12,9
12,4	13,1
13,0	13,5
12,6	12,8

14. В ходе социологического опроса на вопрос о перенесенном в детстве заболе­вании ответы распределились следующим образом:

Есть ли достоверные отличия в ответах женщин и мужчин?

15. Приведены данные ежемесячной результативности (количество голов) фут­больной команды в двух сезонах:

Определите, есть ли статистические различия в ежемесячной результативно­сти команды в рассматриваемых сезонах?

8. Определите, имеют ли выборки {6; 7; 9; 15; 21} и {20; 28; 31; 38; 40} различные уровни разнородности (отличаются ли дисперсии)?

Использование инструмента Пакет анализа для выявления различий между выборками

Для анализа двух выборок с помощью t-теста Стьюдента могут быть использова­ны следующие процедуры: Парный двухвыборочный t-тест для средних; Двухвыбороч­ный t-тест с одинаковыми дисперсиями и Двухвыборочный t-тест с различными дисперсия­ми. Как указывалось в разделе «Анализ двух выборок», в общем случае необходимо воспользоваться процедурой Двухвыборочный t-тест с различными дисперсиями, так как процедуры Парный двухвыборочный t-тест для средних и Двухвыборочный t-тест с одинаковыми дисперсиями относятся к частным, специальным случаям.

Для выполнения процедуры анализа необходимо:

О выполнить команду «Сервис» → «Анализ данных»;

О в появившемся списке Инструменты анализа выбрать строку Двухвыборочный t-тест с различными дисперсиями, щелкнуть левой кнопкой мыши и нажать кнопку 0К;

О в появившемся диалоговом окне указать Интервал переменной 1, то есть ввести ссылку на первый диапазон анализируемых данных, содержащий один столбец данных. Для этого следует навести указатель мыши на верхнюю ячейку перво­го столбца данных, нажать левую кнопку мыши и, не отпуская ее, протянуть указатель мыши к нижней ячейке, содержащей анализируемые данные, затем отпустить левую кнопку мыши;

о указать Интервал переменной 2, то есть ввести ссылку на второй диапазон ана­лизируемых данных, содержащий один столбец данных. Для этого следует на­вести указатель мыши в поле ввода Интервал переменной 2 и щелкнуть левой кнопкой мыши, затем навести указатель мыши на верхнюю ячейку второго стол­бца данных, нажать левую кнопку мыши и, не отпуская ее, протянуть указатель мыши к нижней ячейке, содержащей анализируемые данные, затем отпустить левую кнопку мыши;

О указать выходной диапазон, то есть ввести ссылку на ячейки, в которые будут выведены результаты анализа. Для этого следует поставить флажок в левое поле Выходной диапазон (навести указатель мыши и щелкнуть левой кнопкой), далее навести указатель мыши на правое поле ввода Выходной диапазон и щелкнуть левой кнопкой мыши, затем указатель мыши навести на левую верхнюю ячей­ку выходного диапазона и щелкнуть левой кнопкой мыши. Размер выходного диапазона будет определен автоматически, и на экран будет выведено сообще­ние в случае возможного наложения выходного диапазона на исходные дан­ные.

О нажать кнопку ОК.

Результаты анализа. В выходной диапазон будут выведены: средняя, дисперсия и число наблюдений для каждой переменной, гипотетическая разность средних, df (число степеней свободы), значение t-статистики, Р(Т<= t) одностороннее, t кри­тическое одностороннее, Р(T<= t) двухстороннее, t критическое двухстороннее.

Интерпретация результатов. Если величина вероятности случайного появления анализируемых выборок (P(T<=t) двухстороннее) меньше уровня значимости ( = 0,05), принято считать, что различия между выборками не случайные, то есть различия достоверные.

Пример 1.11. Рассматривается заработная плата обслуживающего персонала и работников ресторана (из примера 1.4).

Персонал	Ресторан
2100	3200
2100	3000
2000	2500
2000	2000
2000	1900
1900	1800
1800
1800

Можно ли по этим данным сделать вывод о большей зарплате работников ресторана?

Решение. Для решения задач такого типа используются так называемые критерии различия, в частности, t-критерий Стьюдента.

1. Введите данные: для персонала — в диапазон А1:А8; работников ресторана -в диапазон В1:В1.

2. Выбор процедуры осуществляется из трех вариантов t-теста. Поскольку дан­ные не имеют попарного соответствия, число их различно и говорить о равен­стве дисперсий затруднительно, выберите процедуру Двухвыборочный t-тест с различными дисперсиями.

Для реализации процедуры в пункте меню Сервис выберите строку Анализ дан­ных и далее укажите курсором мыши на строку Двухвыборочный t-тест с различ­ными дисперсиями.

3. В появившемся диалоговом окне задайте Интервал переменной 1. Для этого на­ведите указатель мыши на верхнюю ячейку столбца (А1), нажмите левую кноп­ку мыши и, не отпуская ее, протяните указатель мыши к нижней ячейке (А8) затем отпустите левую кнопку мыши.

4. Аналогично укажите Интервал переменной 2, то есть введите ссылку на диапа­зон второго столбца В1:В1.

5. Далее укажите выходной диапазон. Для этого поставьте переключатель в поло­жение Выходной диапазон (наведите указатель мыши и щелкните левой кноп­кой), затем наведите указатель мыши на правое поле ввода Выходной диапазон, щелкнув левой кнопкой мыши, указатель мыши наведите на левую верхнюю ячейку выходного диапазона (С1). Щелкните левой кнопкой мыши и нажмите кнопку ОК.

Результаты анализа. В выходном диапазоне С1:Е13 появятся результаты процеду­ры Двухвыборочный t-тест с различными дисперсиями (рис. 1.16).

	A	B	C	D	F
1	2100	3200	Двухвыборочный t-тест с различными дисперсиями
2	2100	3000
3	2000	2500		Переменная 1	Переменная 2
4	2000	2000	Среднее	1962,5	2400
5	2000	1900	Дисперсия	14107,14286	356000
6	1900	1800	Наблюдения	8	6
7	1800		Гипотетическая разность средних	0
8	1800		df	5
9			t-статистика	-1,769982969
10			P(T<=t) одностороннее	0,068475305
11			t критическое одностороннее	2,015049176
12			P(T<=t) двухстороннее	0,13695061
13			t критическое двухстороннее	2,570577635

Рис. 1.16. Исходные данные (А1:В8) и результаты анализа (С1:Е13) из примера 1.11

Интерпретация результатов. Средние значения заработной платы (1962 руб персонала и 2400 руб. для работников ресторана) довольно сильно отличаются. Тем не менее нулевая гипотеза о том, что разницы между группами нет (то есть средние выборок равны между собой), отвергнута быть не может. Это следует из того, что вероятность реализации нулевой гипотезы достаточно велика (р = 0,1389, что больше чем уровень значимости 0,05, то есть р > 0,05) и величина вероятности случайного появления анализируемых выборок (P(T<=t) двухстороннее) боль­ше уровня значимости ( = 0,05). А это позволяет говорить, что различия между выборками могут быть случайными, то есть различия недостоверные.

Таким образом, из полученных результатов исследования вытекает, что на осно­вании приведенных данных нельзя сделать вывод о достоверно большей зарплате работников ресторана.

Упражнения

17. Определите, достоверны ли различия в количестве приобретаемых туристских путевок семейными парами и отдельными туристами.

Количество приобретаемых путевок
Месяцы 1 2 3 4 5 6

Пары 67 75 58 89 96 94

Одиночки 43 56 78 87 85 90

18. В таблице приведены результаты группы студентов по скоростному чтению до и после специального курса по быстрому чтению.

Студент 12345678910

До курса 86 83 86 70 66 90 70 85 77 86

После 82 79 91 77 68 86 81 90 85 94

Произошли ли статистически значимые изменения скорости чтения у студентов?

Дисперсионный анализ

В случае необходимости оценить достоверность различия между несколькими груп­пами наблюдений (выборками) используют методы дисперсионного анализа.

Дисперсионный анализ предназначен для исследования задачи о действии на из­меряемую случайную величину (отклик) одного или нескольких независимых факторов, имеющих несколько градаций. Причем в однофакторном, двухфакторном и т. д. анализе влияющие на результат факторы считаются известными, и речь идет только о выяснении существенности или оценке этого влияния.

Применение дисперсионного анализа возможно, если можно предполагать соот­ветствие выборочных групп генеральным совокупностям с нормальным распреде­лением и независимость распределений наблюдений в группах.

В дальнейшем ограничимся рассмотрением простейшего случая дисперсионного анализа − однофакторного анализа. При этом задача заключается в том, чтобы сравнить дисперсию, обусловленную случайными причинами, с дисперсией, вызываемой наличием исследуемого фактора. Если они значимо различаются, то считают, что фактор оказывает статистически значимое влияние на исследуемую переменную. Значимость различий проверяется по критерию Фишера.

Влияние случайной составляющей характеризуют внутригрупповая дисперсия влияние изучаемого фактора − межгрупповая. Внутригрупповая дисперсия рас­считывается по формуле:

межгрупповая:

Здесь М − общее среднее, Мm − количество групп, n − количество элементов в группе.

В MS «MS Excel» для проведения однофакторного дисперсионного анализа использует­ся процедура Однофакторный дисперсионный анализ.

Для проведения дисперсионного анализа необходимо:

О ввести данные в таблицу, так чтобы в каждом столбце оказались данные, соот­ветствующие одному значению исследуемого фактора, а столбцы располагали в порядке возрастания (убывания) величины исследуемого фактора;

О выполнить команду Сервис → Анализ данных;

О в появившемся диалоговом окне «Анализ данных» в списке «Инструменты анализа» выбрать процедуру «Однофакторный дисперсионный анализ», указав курсором мы; и щелкнув левой кнопкой мыши. Затем нажать кнопку ОК;

О в появившемся диалоговом окне задать Входной интервал, то есть ввести ссылку на диапазон анализируемых данных, содержащий все столбцы данных. Для этого следует навести указатель мыши на верхнюю левую ячейку диапазона данных, нажать левую кнопку мыши и, не отпуская ее, протянуть указатель мыши и нижней правой ячейке, содержащей анализируемые данные, затем отпустить левую кнопку мыши (рис. 1.17);

О в разделе «Группировка» переключатель установить в положение по столбцам:

О указать выходной диапазон, то есть ввести ссылку на ячейки, в которые будут выведены результаты анализа. Для этого следует поставить переключатель в положение Выходной интервал (навести указатель мыши и щелкнуть левой кноп­кой), далее навести указатель мыши на правое поле ввода Выходной интервал: щелкнуть левой кнопкой мыши, затем указатель мыши навести на левую верхнюю ячейку выходного диапазона и щелкнуть левой кнопкой мыши. Размер выходного диапазона будет определен автоматически, и на экран будет выведено сообщение в случае возможного наложения выходного диапазона на и исходные данные.

О нажать кнопку ОК.

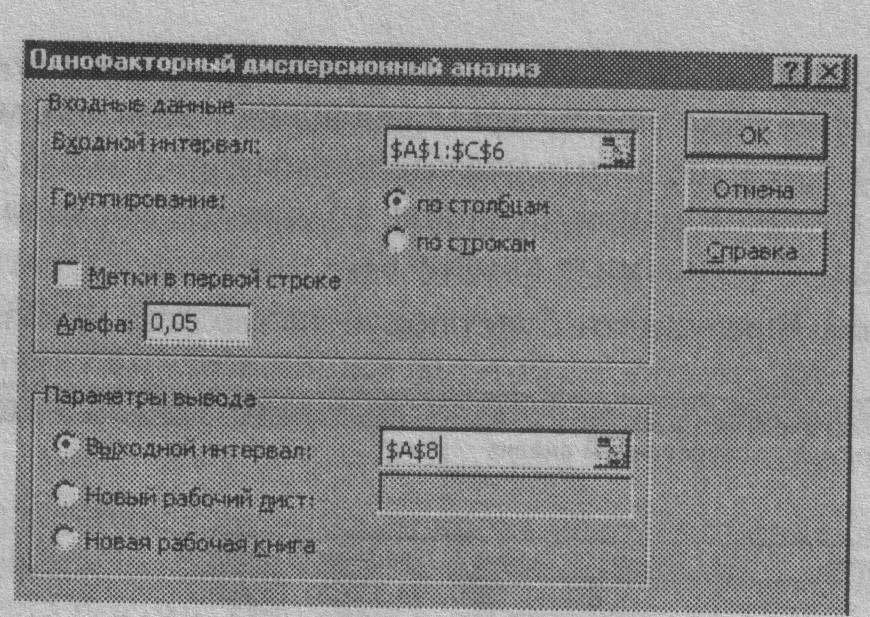
Рис. 1.17. Пример заполнения диалогового окна Однофакторный дисперсионный анализ

Результаты анализа. Выходной диапазон будет включать в себя результаты дис­персионного анализа: средние, дисперсии, критерий Фишера и другие показатели.

Интерпретация результатов. Влияние исследуемого фактора определяется по величине значимости критерия Фишера, которая находится в таблице Дисперси­онный анализ на пересечении строки Между группами и столбца Р-Значение. В случа­ях, когда Р-Значение < 0,05, критерий Фишера значим и влияние исследуемого фак­тора можно считать доказанным.

Кроме рассмотренной процедуры однофакторного дисперсионного анализа, для проведения двухфакторного дисперсионного анализа в пакете анализа реализова­ны процедуры Двухфакторный дисперсионный анализ с повторениями и Двухфакторный дисперсионный анализ без повторений.

Пример 1.12. Необходимо выявить, влияет ли расстояние от центра города на степень заполняемости гостиниц. Пусть введены 3 уровня расстояний от центра города: 1) до 3 км, 2) от 3 до 5 км и 3) свыше 5 км. Данные заполняемости представлены в таблице.

Расстояние	Заполняемость %
До 3 км.	92	98	89	97	90	94
От 3 до 5 км.	90	86	84	91	83	82
Свыше 5 км.	87	79	74	85	73	77

Решение

1. Исследуемые данные введите в рабочую таблицу «MS Excel» по столбцам: в столбец А − заполняемость гостиниц в центре города, в столбец В − гостиниц, находя­щихся на расстоянии от 3 до 5 км и т. д. (диапазон А1:С6).

2. Выполните команду «Сервис» → «Анализ данных». В появившемся диалоговом окне Анализ данных в списке Инструменты анализа щелчком мыши выберите процеду­ру Однофакторный дисперсионный анализ. Нажмите кнопку ОК.

3. В появившемся диалоговом окне «Однофакторный дисперсионный анализ» в поле «Входной интервал» задайте А1:С1. Для этого наведите указатель мыши на ячейку А1 и протяните его к ячейке С6 при нажатой левой кнопке мыши.

4. В разделе «Группировка» переключатель установите в положение по столбцам.

5. Далее необходимо указать выходной диапазон. Для этого поставьте переклю­чатель в положение Выходной интервал (наведите указатель мыши и щелкните левой кнопкой), затем щелкните указателем мыши в правом поле ввода Выход­ной интервал, и щелчком мыши на ячейке А8 укажите расположение выходного диапазона (рис. 1.17). Нажмите кнопку ОК.

Результаты анализа. В результате будет получена таблица, показанная на рис. 1.18.

Однофакторный дисперсионный анализ
ИТОГИ
Группы	Счет	Сумма	Среднее	Дисперсия
Столбец 1	6	560	93,33333	13,4667
Столбец 2	6	516	86	14
Столбец 3	6	475	79,1667	32,9667
Дисперсионный анализ
Источник вариации	SS	df	MS	F	P-Значение	F критическое
Между группами	602,3	2	301,166	14,95036	0,0002684	3,6823166
Внутри групп	302,1	15	20,144
Итого	904,5	17

Рис. 1.18. Результат работы инструмента Однофакторный дисперсионный анализ

Интерпретация результатов. В таблице «Дисперсионный анализ» на пересечении строки Между группами и столбца Р-Значение находится величина 0,0002684. Величина Р-Значение < 0,05, следовательно, критерий Фишера значим и влияние фактора расстоя­ния от центра города на эффективность заполнения гостиниц доказано статистически.

Упражнение

19. Определите, влияет ли фактор образования на уровень зарплаты в гостинице на основании следующих данных:

Образование	Зарплата сотрудника
высшее	3200 3000 2600 2000 1900 1900
среднее спец	2600 2000 2000 1900 1800 1800
среднее	2000 2000 1900 1800 1700 1700

Корреляционный анализ

Важным разделом статистического анализа является корреляционный анализ, слу­жащий для выявления взаимосвязей между выборками.

Коэффициент корреляции

Выявление взаимосвязей. Одна из наиболее распространенных задач статисти­ческого исследования состоит в изучении связи между некоторыми наблюдаемыми переменными. Знание взаимозависимостей отдельных признаков дает возмож­ность решать одну из кардинальных задач любого научного исследования: возмож­ность предвидеть, прогнозировать развитие ситуации при изменении конкретных характеристик объекта исследования. Например, основное содержание любой эко­номической политики, в конечном счете, может быть сведено к регулированию эко­номических переменных, осуществляемому на базе выявленной тем или иным обра­зом информации об их взаимовлиянии. Поэтому, проблема изучения взаимосвязей показателей различного рода является одной из важнейших в статистическом ана­лизе.

Обычно взаимосвязь между выборками носит не функциональный, а вероятност­ный (или стохастический) характер. В этом случае нет строгой, однозначной зави­симости между величинами. При изучении стохастических зависимостей разли­чают корреляцию и регрессию.

Регрессионный анализ (см. раздел «Регрессионный анализ») устанавливает фор­мы зависимости между случайной величиной Y и значениями одной или несколь­ких переменных величин.

Корреляционный анализ состоит в определении степени связи между двумя слу­чайными величинами X и Y. В качестве меры такой связи используется коэффи­циент корреляции. Коэффициент корреляции оценивается по выборке объема п связанных пар наблюдений (х_i y_i) из совместной генеральной совокупности X и Y. Существует несколько типов коэффициентов корреляции, применение которых зависит от предположений о совместном распределении величин X и Y.

Для оценки степени взаимосвязи наибольшее распространение получил коэффи­циент линейной корреляции (Пирсона), предполагающий нормальный закон рас­пределения наблюдений.

Коэффициент корреляции (R, r) − параметр, характеризующий степень линей­ной взаимосвязи между двумя выборками. Коэффициент корреляции изменяется от -1 (строгая обратная линейная зависимость) до 1 (строгая прямая пропорцио­нальная зависимость). При значении 0 линейной зависимости между двумя вы­борками нет. Здесь под прямой зависимостью понимают зависимость, при кото­рой увеличение или уменьшение значения одного признака ведет, соответственно, к увеличению или уменьшению второго. Например, при увеличении температуры возрастает давление газа, а при уменьшении − снижается (при постоянном объе­ме). При обратной зависимости увеличение одного признака приводит к умень­шению второго и наоборот. Примером обратной корреляционной зависимости может служить связь между температурой воздуха на улице и количеством топли­ва, расходуемого на обогрев помещения.

Выборочный коэффициент линейной корреляции между двумя случайными ве­личинами X и Y рассчитывается по формуле

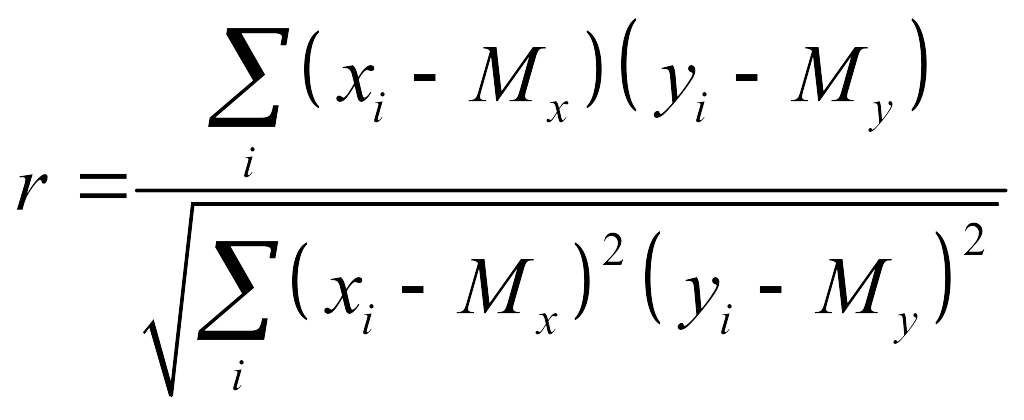
Коэффициент корреляции является безразмерной величиной и его значение не зависит от единиц измерения случайных величин X и Y.

На практике коэффициент корреляции принимает некоторые промежуточные значения между 1 и -1 (рис. 1.19). Для оценки степени взаимосвязи можно руководствоваться следующими эмпирическими правилами. Если коэффициент корреляции (r) по абсолютной величине (без учета знака) больше, чем 0,95, то принято считать, что между параметрами существует практически линейная зависимость, (прямая − при положительном r и обратная − при отрицательном r). Если коэффициент корреляции r лежит в диапазоне от 0,8 до 0,95, говорят о сильной степени линейной связи между параметрами. Если 0,6 < \r\ < 0,8, говорят о наличии линейной связи между параметрами. При \r\ < 0,4 обычно считают, что линейная взаимосвязь между параметрами выявить не удалось.

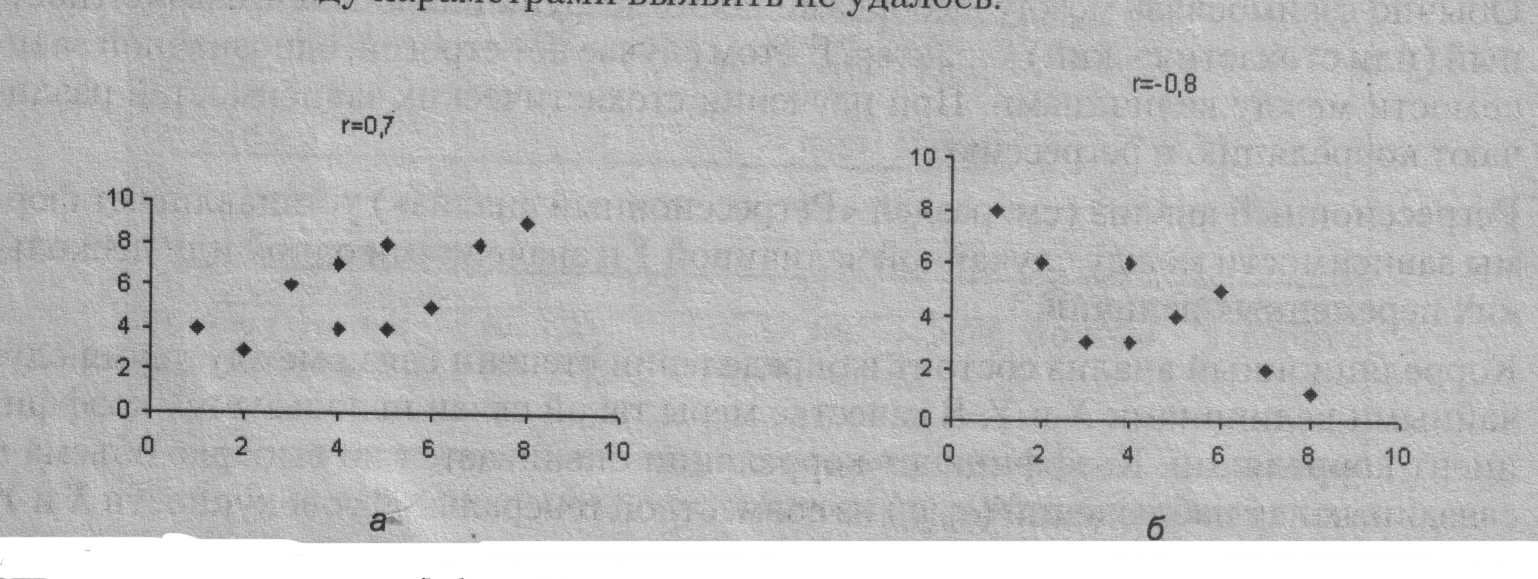
Рис. 1.19. Примеры прямой (r» 0,7, а) и обратной (r= -0,8, б) корреляционной зависимости

О В MS «MS Excel» для вычисления парных коэффициентов линейной корреляции используется специальная функция К0РРЕЛ. Параметрами функции являются К0РРЕЛ(масив1;массив2), где: массив1 — это диапазон ячеек первой случайной величины;

О массив2 − это второй интервал ячеек со значениями второй случайной величины.

Пример 1.13. Имеются результаты семимесячных наблюдений реализации путевок двух туристских маршрутов тура А и тура В.

Тур А	Тур В
120	20
121	15
105	18
92	16
113	19
90	16
80	15

Необходимо определить, имеется ли взаимосвязь между количеством продаж путевок обоих маршрутов.

Решение

Для выявления степени взаимосвязи, прежде всего, необходимо ввести данные в рабочую таблицу.

Откройте новую рабочую таблицу. Введите в ячейку А1 слова Тур А. Затем в ячейки А2:А8 − соответствующие значения числа продаж. В ячейки В1:В8 введите название и значения для тура В. Затем вычисляется значение коэффициента корреляции между выборками. Для этого табличный курсор установите в свободную ячейку (А9). На панели инструментов нажмите кнопку Вставка функции (f_x). В появившемся диалоговом окне Мастер функций выберите ка­тегорию Статистические и функцию КОРРЕЛ, после чего нажмите кнопку ОК. Появив­шееся диалоговое окно КОРРЕЛ за серое поле мышью отодвиньте вправо на 1-2 см от данных (при нажатой левой клавише). Указателем мыши введите диапазон дан­ных Тур А в поле Массив 1 (А2:А8). В поле Массив 2 введите диапазон данных Тур В (В2:В8). Нажмите кнопку ОК. В ячейке А9 появится значение коэффициента кор­реляции − 0,995493. Значение коэффициента корреляции больше чем 0,95. Зна­чит, можно говорить о том, что в течение периода наблюдения имелась высокая степень прямой линейной взаимосвязи между количествами проданных путевок обоих маршрутов (r= 0,557292).

Корреляционная матрица

При большом числе наблюдений, когда коэффициенты корреляции необходимо по­следовательно вычислять из нескольких рядов числовых данных, для удобства полу­чаемые коэффициенты сводят в таблицы, называемые корреляционными матрицами.

Корреляционная матрица − это квадратная (или прямоугольная) таблица, в кото­рой на пересечении соответствующих строки и столбца находится коэффициент корреляции между соответствующими параметрами.

В MS «MS Excel» для вычисления корреляционных матриц используется процедура Корреляция. Процедура позволяет получить корреляционную матрицу, содержащую коэффициенты корреляции между различными параметрами.

Для реализации процедуры необходимо:

О выполнить команду Сервис → Анализ данных;

О в появившемся списке Инструменты анализа выбрать строку Корреляция и нажать кнопку ОК;

О в появившемся диалоговом окне указать Входной интервал, то есть ввести ссыл­ку на ячейки, содержащие анализируемые данные. Для этого следует навести указатель мыши на левую верхнюю ячейку данных, нажать левую кнопку мыши и, не отпуская ее, протянуть указатель мыши к правой нижней ячейке, содер­жащей анализируемые данные, затем отпустить левую кнопку мыши. Входной интервал должен содержать не менее двух столбцов.

О в разделе Группировка переключатель установить в соответствии с введенными данными;

О указать выходной диапазон, то есть ввести ссылку на ячейки, в которые будут вы­ведены результаты анализа. Для этого следует поставить флажок в левое поле Вы­ходной интервал (навести указатель мыши и щелкнуть левой кнопкой), далее наве­сти указатель мыши на правое поле ввода Выходной интервал и щелкнуть левой кнопкой мыши, затем указатель мыши навести на левую верхнюю ячейку выход­ного диапазона и щелкнуть левой кнопкой мыши. Размер выходного диапазона будет определен автоматически, и на экран будет выведено сообщение в случае возможного наложения выходного диапазона на исходные данные (рис. 1.20).

О нажать кнопку ОК.

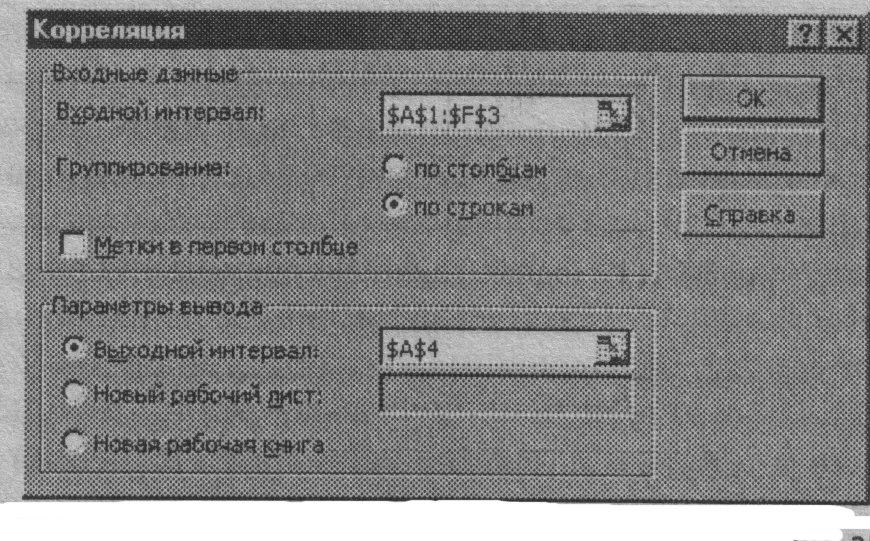
Рис. 1.20. Пример установки параметров корреляционного анализа

Результаты анализа. В выходной диапазон будет выведена корреляционная мат­рица, в которой на пересечении каждых строки и столбца находится коэффи­циент корреляции между соответствующими параметрами. Ячейки выходного диапазона, имеющие совпадающие координаты строк и столбцов, содержат зна­чение 1, так как каждый столбец во входном диапазоне полностью коррелирует с самим собой.

Интерпретация результатов. Рассматривается отдельно каждый коэффици­ент корреляции между соответствующими параметрами. Его числовое значе­ние оценивается по эмпирическим правилам, изложенным в разделе «Коэффи­циент корреляции». Отметим, что хотя в результате будет получена треугольная матрица, корреляционная матрица симметрична, и коэффициенты корреляции

r_ij=r_ji.

Пример 1.14. Имеются ежемесячные данные наблюдений за состоянием погоды и посещаемостью музеев и парков.

Число ясных дней Количество посетителей музея Количество посетителей парка

8 8	495 495	132 132
14	503	348
20	380	643
25	305	865
20	348	743
15	465	541

Необходимо определить, существует ли взаимосвязь между состоянием погоды и посещаемостью музеев и парков.

Решение. Для выполнения корреляционного анализа введите в диапазон А1:С3 исходные данные (рис. 1.21).

Затем в меню Сервис выберите пункт Анализ данных и далее укажите строку Корреляция. В появившемся диалоговом окне укажите Входной интервал В1:G3. Укажите, что данные рассматриваются по строкам. Укажите выходной диапазон. Для этого поставьте флажок в левое поле Выходной интервал и в правое поле ввода Выходной интервал введите А4 (рис. 1.20). Нажмите кнопку ОК.

	A	B	C	D	E	F	G
1	Ясные дни	8	14	20	25	20	15
2	Посещаемость музея	495	503	380	305	348	465
3	Посещаемость парка	132	348	643	865	743	541

Рис. 1.21. Исходные данные из примера 1.14

	Строка 1	Строка 2	Строка 3
Строка 1	1
Строка 2	-0,921	1
Строка 3	0,974	-0,919	1

Рис. 1.22. Результаты вычисления корреляционной матрицы из примера 1.14

Результаты анализа. В выходном диапазоне получаем корреляционную матрицу (рис. 1.22).

Интерпретация результатов. Из таблицы видно, что корреляция между со­стоянием погоды и посещаемостью музея равна -0,92, а между состоянием по­годы и посещаемостью парка −0,97, между посещаемостью парка и музея − r=-0,92.

Таким образом, в результате анализа выявлены зависимости: сильная степень об­ратной линейной взаимосвязи между посещаемостью музея и количеством сол­нечных дней (r =-0,92) и практически линейная (очень сильная прямая) связь между посещаемостью парка и состоянием погоды (r = 0,97). Между посещаемостью музея и парка имеется сильная обратная взаимосвязь (r= -0,92).

Подразумевается, что в пустых клетках в правой верхней половине таблицы нахо­дятся те же коэффициенты корреляции, что и в нижней левой (симметрично рас­положенные относительно диагонали).

Упражнения

20. Определите, имеется ли взаимосвязь между рождаемостью и смертностью (ко­личество на 1000 человек) в Санкт-Петербурге:

Годы	Рождаемость	Смертность
1991	9,3	12,5
1992	7,4	13,5
1993	6,6	17,4
1994	7,1	17,2
1995	7,0	15,9
1996	6,6	14,2

21. Определите, имеется ли взаимосвязь между годовым уровнем инфляции (%), ставкой рефинансирования (%) и курсом доллара (руб./$), по следующим дан­ным ежегодных наблюдений:

Уровень инфляции Ставка рефинансирования Курс $

84 85 6,3

45 55 14

56 65 20

34 40 28

23 28 29

Регрессионный анализ

При исследовании взаимосвязей между выборками помимо корреляции различают также и регрессию. Регрессия используется для анализа воздействия на отдельную зависимую переменную значений одной или более независимых переменных. Соответственно, наряду с корреляционным анализом еще одним инструментом ^-изучения стохастических зависимостей является регрессионный анализ.

Регрессионный анализ устанавливает формы зависимости между случайной величиной Y (зависимой) и значениями одной или нескольких переменных величин (независимых), причем значения последних считаются точно заданными. Такая зависимость обычно определяется некоторой математической моделью (уравнением регрессии), содержащей несколько неизвестных параметров. В ходе регрессионного анализа на основании выборочных данных находят оценки этих параметров, определяются статистические ошибки оценок или границы доверитель интервалов и проверяется соответствие (адекватность) принятой математической модели экспериментальным данным.

В линейном регрессионном анализе связь между случайными величинами предполагается линейной. В самом простом случае в линейной регрессионной модели имеются две переменные X и Y. И требуется по п парам наблюдений (X₁,Y₁), (Х₂, Y₂),…,(Х_n Y_n) построить (подобрать) прямую линию, называемую линией регрессии, которая «наилучшим образом» приближает наблюдаемые значения. Yравнение этой линии Y = аХ + b является регрессионным уравнением. С помощью_ регрессионного уравнения можно предсказать ожидаемое значение зависимости личины Y₀, соответствующее заданному значению независимой переменной Х₀.

Таким образом, можно сказать, что линейный регрессионный анализ заключало в подборе графика и его уравнения для набора наблюдений. В регрессионном анализе все признаки (переменные), входящие в уравнение, должны иметь непрерывную, а не дискретную природу.

В случае, когда рассматривается зависимость между одной зависимой переменной

Y и несколькими независимыми Х_и Х₂,..., Х_n, говорят о множественной линейной

регрессии. В этом случае регрессионное уравнение имеет вид

Y = а₀ + a₁ X₁ + а₂Х₂ +... + а_пХ_n

где а₁, а₂, ..., а_n − требующие определения коэффициенты при независимых переменных Х₁, Х₂, ...,Х_п а₀ − константа.Мерой эффективности регрессионной модели является коэффициент детермина­ции R² (R-квадрат). Коэффициент детерминации (R-квадрат) определяет, с какой степенью точности полученное регрессионное уравнение описывает (аппроксими­рует) исходные данные.

Исследуется также значимость регрессионной модели с помощью F-критерия (Фи­шера). Если величина F-критерия значима (р < 0,05), то регрессионная модель яв­ляется значимой.

Достоверность отличия коэффициентов a₀, а₁, а_2, а_n от нуля проверяется с по­мощью критерия Стьюдента. В случаях, когда р > 0,05, коэффициент может считаться нулевым, а это означает, что влияние соответствующей независимой пере­менной на зависимую переменную недостоверно, и эта независимая переменная может быть исключена из уравнения.

В MS «MS Excel» экспериментальные данные аппроксимируются линейным уравнени­ем до 16 порядка: У= а₀ + a₁X₁ + а₂Х₂ + ... + а_nХ_n,

где Y− зависимая переменная, X1, ...,Хn − независимые переменные, а0, а1, ..., аn − искомые коэффициенты регрессии.

Для получения коэффициентов регрессии используется процедура Регрессия из пакета анализа. Кроме того, могут быть использованы функция Л ИНЕЙН для полу­чения параметров регрессионного уравнения и функция ТЕНДЕНЦИЯ для получе­ния предсказанных значений Y в требуемых точках (см. раздел «Несколько неза­висимых переменных» главы 3).

Для реализации процедуры Регрессия необходимо:

О выполнить команду «Сервис» → «Анализ данных»;

О в появившемся диалоговом окне Анализ данных в списке Инструменты анализа выбрать строку Регрессия, указав курсором мыши и щелкнув левой кнопкой мыши. Затем нажать кнопку 0К;

О в появившемся диалоговом окне задать Входной интервал Y, то есть ввести ссыл­ку на диапазон анализируемых зависимых данных, содержащий один столбец данных. Для этого следует навести указатель мыши на верхнюю ячейку столб­ца зависимых данных, нажать левую кнопку мыши и, не отпуская ее, протянуть указатель мыши к нижней ячейке, содержащей анализируемые данные, затем отпустить левую кнопку мыши;

О указать Входной интервал X, то есть ввести ссылку на диапазон независимых данных, содержащий до 16 столбцов анализируемых данных. Для этого следует навести указатель мыши на поле ввода Входной интервал X и щелкнуть левой кнопкой мыши, затем навести указатель мыши на верхнюю левую ячейку диа­пазона независимых данных, нажать левую кнопку мыши и, не отпуская ее, протянуть указатель мыши к нижней правой ячейке, содержащей анализируе­мые данные, затем отпустить левую кнопку мыши;

О указать выходной диапазон, то есть ввести ссылку на ячейки, в которые будут выведены результаты анализа. Для этого следует поставить переключатель в положение Выходной интервал (навести указатель мыши и щелкнуть левой кнопкой), далее навести указатель мыши на правое поле ввода Выходной интервал и щелкнуть левой кнопкой мыши, затем указатель мыши навести на левую верх­нюю ячейку выходного диапазона и щелкнуть левой кнопкой мыши (рис. 1.23). Размер выходного диапазона будет определен автоматически, и на экран будет выведено сообщение в случае возможного наложения выходного диапазона на исходные данные;