ВУЗ: Томский государственный университет систем управления и радиоэлектроники
Категория: Учебное пособие
Дисциплина: Электроника
Добавлен: 23.10.2018
Просмотров: 11045
Скачиваний: 27

96
достаточно
большом
токе
всегда
превалирует
напряжение
Б
U
и
экспоненциальная
характеристика
диода
вырождается
.
Следует
указать
,
что
дифференциальное
и
статическое
со
-
противления
диодов
могут
существенно
отличаться
от
аналогич
-
ных
сопротивлений
,
вычисленных
для
перехода
,
из
-
за
влияния
сопротивления
базы
.
2.6
Переходные
характеристики
плоскостного
диода
Наличие
реактивных
компонентов
(
паразитные
емкости
и
индуктивности
)
приводит
к
появлению
переходных
процессов
в
устройствах
,
что
ограничивает
их
быстродействие
и
уменьшает
полосу
пропускания
.
Полупроводниковый
диод
также
является
инерционным
элементом
по
отношению
к
быстрым
изменениям
тока
или
на
-
пряжения
,
поскольку
новое
распределение
носителей
устанавли
-
вается
не
сразу
.
Индуктивностями
выводов
пренебрегаем
.
Как
известно
,
внешнее
напряжение
приводит
к
изменению
ширины
перехода
,
а
значит
,
и
величины
пространственных
зарядов
в
пе
-
реходе
.
Кроме
того
,
при
инжекции
(
или
экстракции
)
меняются
заряды
в
области
базы
.
Следовательно
,
наряду
с
проводимостью
,
которая
в
первом
приближении
характеризуется
выражением
(2.23),
диод
обладает
емкостью
,
которую
можно
считать
подклю
-
ченной
параллельно
-
p n
переходу
.
Эту
емкость
принято
разде
-
лять
на
две
составляющие
:
барьерную
емкость
,
отражающую
пе
-
рераспределение
зарядов
в
переходе
,
и
диффузионную
емкость
,
отражающую
перераспределение
зарядов
в
базе
.
Понятие
диффу
-
зионная
емкость
является
вообще
-
то
условным
,
т
.
к
.
физически
этой
емкости
нет
.
Введение
понятия
«
диффузионная
емкость
»
позволяет
проводить
аналитические
расчеты
,
не
прибегая
к
рас
-
чету
распределения
носителей
в
базе
.
Такое
разделение
,
в
общем
,
весьма
условно
,
но
удобно
на
практике
,
тем
более
что
соотноше
-
ние
обеих
емкостей
различно
при
разных
полярностях
смещения
.
При
прямом
смещении
главную
роль
играют
заряды
в
базе
и
соответственно
диффузионная
емкость
.
При
обратном
смещении
(
режим
экстракции
)
заряды
в
базе
меняются
мало
,
и
главную
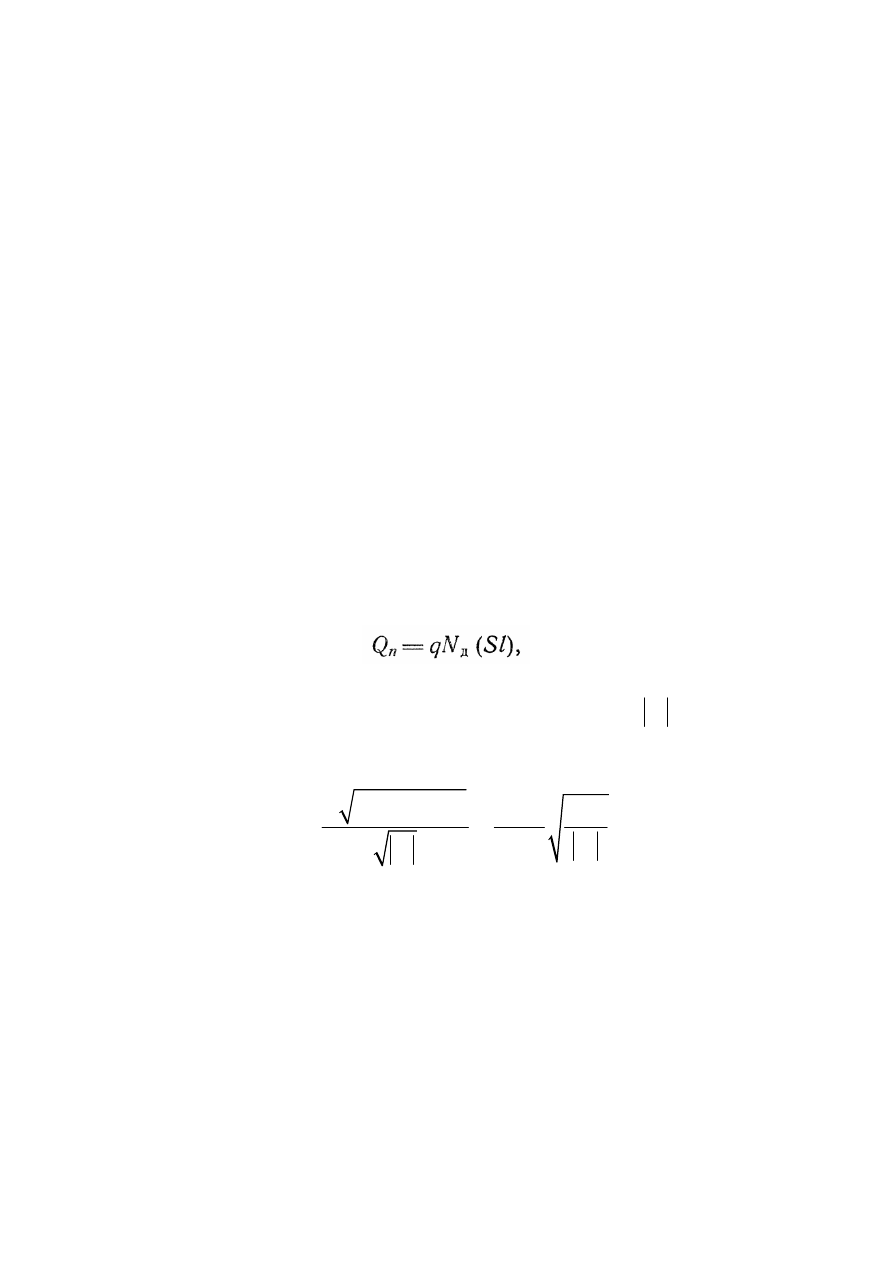
97
роль
играет
барьерная
емкость
.
Характеристика
инерционных
свойств
диода
с
помощью
емкостей
особенно
удобна
в
случае
малых
переменных
сигналов
,
действующих
на
фоне
больших
по
-
стоянных
смещений
.
При
этом
емкости
оказываются
почти
ли
-
нейными
и
весьма
наглядно
дополняют
эквивалентную
схему
диода
.
В
случае
больших
сигналов
использование
емкостей
,
осо
-
бенно
диффузионной
,
становится
нецелесообразным
,
так
как
их
нелинейность
проявляется
в
такой
мере
,
что
эквивалентная
схема
теряет
свою
наглядность
,
а
анализ
делается
отнюдь
не
более
про
-
стым
,
чем
при
использовании
уравнений
непрерывности
.
После
этих
предварительных
замечаний
мы
рассмотрим
сначала
свойст
-
ва
барьерной
и
диффузионной
емкостей
,
а
затем
исследуем
пере
-
ходный
процесс
при
большом
сигнале
.
Барьерная емкость (емкость перехода).
Определим
вели
-
чину
барьерной
емкости
,
считая
,
что
переход
несимметричен
и
сосредоточен
в
базе
типа
.
Заряды
на
пластинах
воображаемого
конденсатора
—
перехода
—
одинаковы
(
)
p
n
Q
Q
−
=
.
Найдем
один
из
них
,
например
n
Q ,
для
случая
ступенчатого
перехода
где
S —
площадь
перехода
;
l —
ширина
перехода
.
Подставляя
сюда
выражение
(2.12)
и
дифференцируя
(
n
Q )
по
U ,
получаем
дифференциальную
барьерную
емкость
ступенчатого
перехода
при
обратном
смещении
0
0
0
0
0,5
.
Д
П
S
qN
S
C
l
U
U
ξξ
ξξ
Δϕ
=
=
(2.43
а
)
Вторая
форма
выражения
удобна
тем
,
что
ее
первый
множи
-
тель
является
емкостью
обычного
плоского
конденсатора
с
рас
-
стоянием
между
пластинами
,
равным
0
l —
равновесной
ширине
перехода
,
определяемой
по
формуле
(2.9
б
).
Как
видим
,
емкость
пе
-
рехода
зависит
от
приложенного
напряжения
.
Величина
барьерной
емкости
современных
диодов
лежит
в
пределах
(
)
2
200
−
пф
.
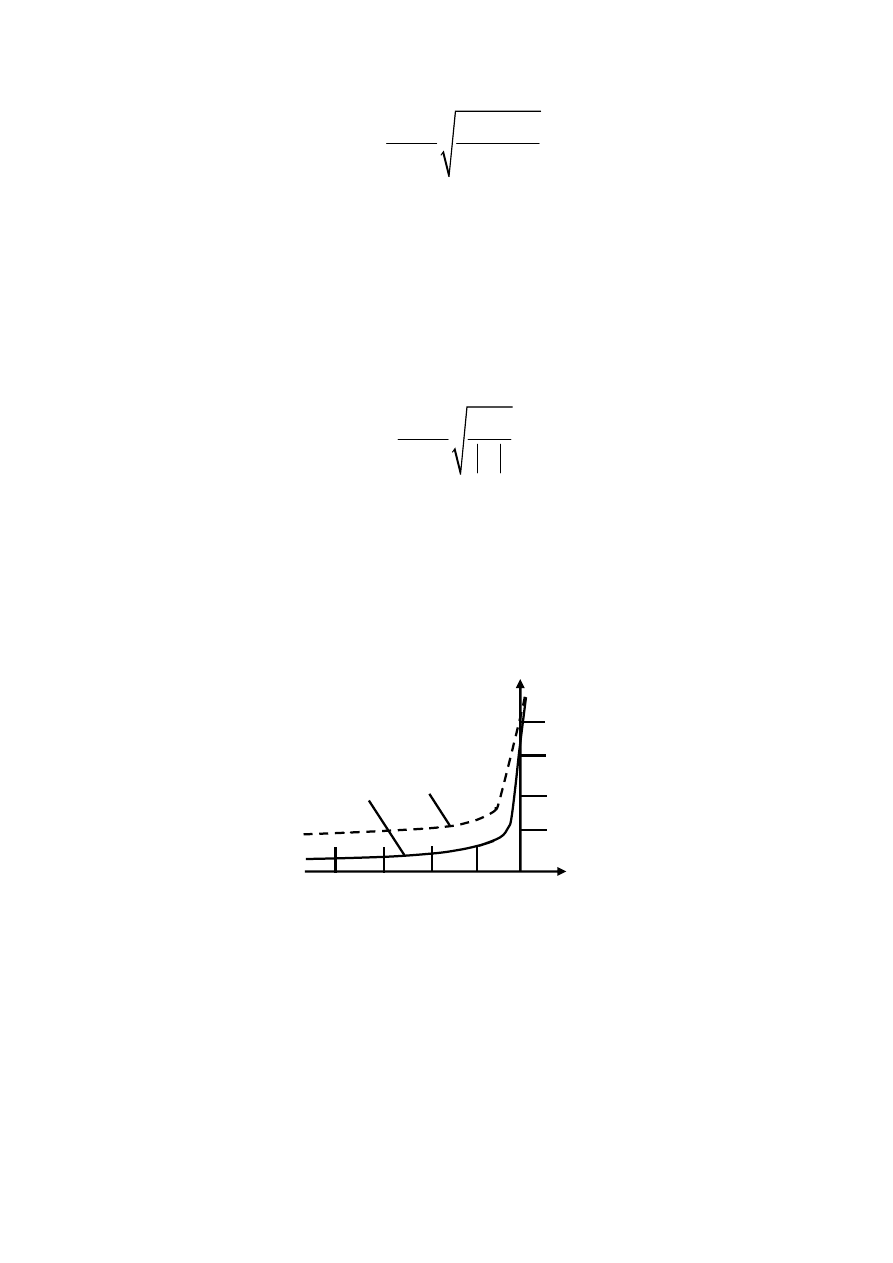
В
общем
случае
,
используя
(2.11),
для
барьерной
емкости
будем
иметь
:
98
0
0
0
0
.
П
S
C
l
U
ξξ
Δϕ
=
Δϕ −
(2.436)
Эта
формула
может
давать
большую
погрешность
при
пря
-
мых
напряжениях
(более 0,1 — 0,2) В
,
так
как
в
исходных
выра
-
жениях
(2.9)
не
учтен
заряд
подвижных
носителей
в
переходе
,
существенный
при
прямых
смещениях
.
Необходимо заметить,
что изменение ширины перехода (т.е. перезаряд емкости) тре-
бует притока или отвода основных (для каждого слоя) носи-
телей. Отсюда следует, что на высоких частотах должен
уменьшаться коэффициент инжекции неосновных носителей.
0
0
3
0
.
П
S
C
l
U
ξξ
Δϕ
=
(2.43
в
)
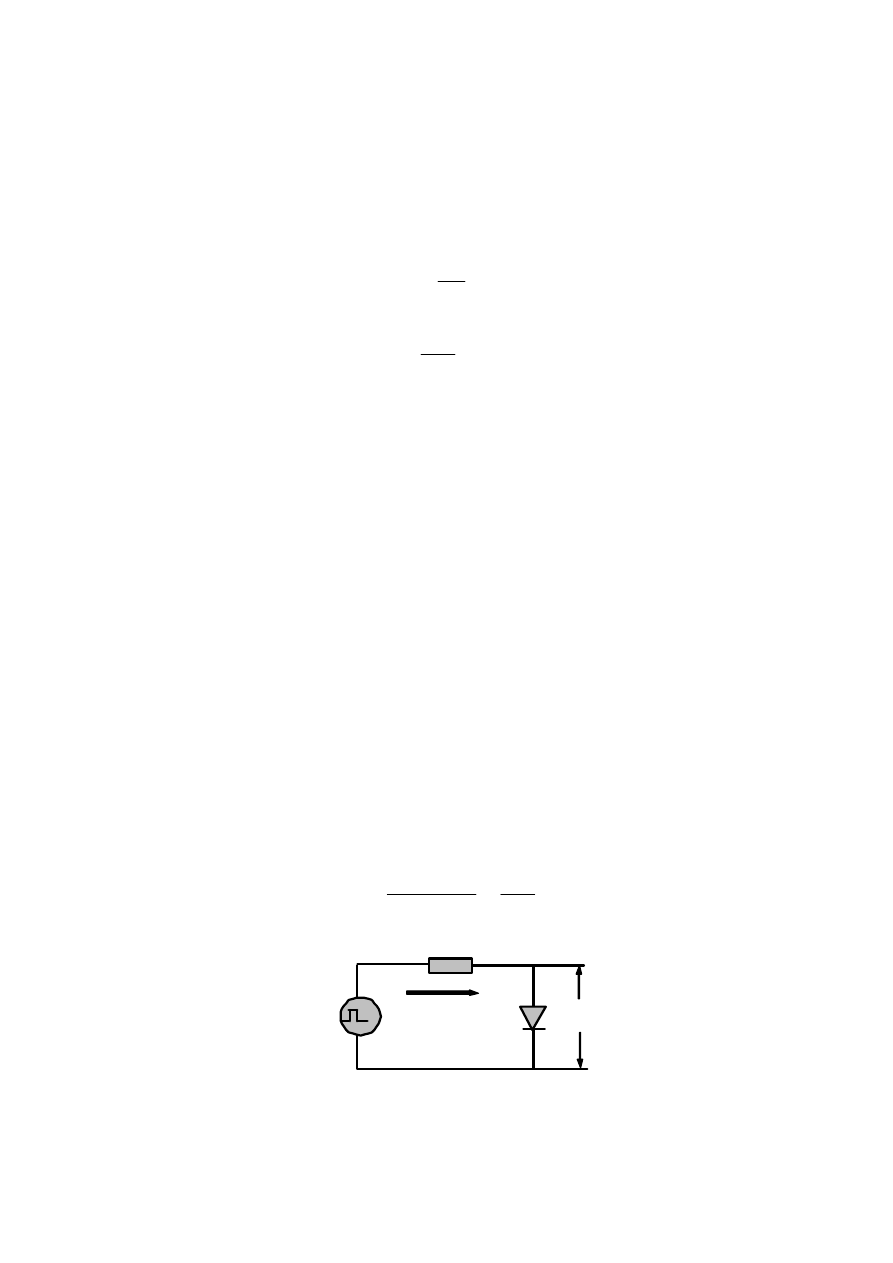
Зависимость
барьерных
емкостей
от
обратного
напряжения
показана
на
рис
. 2.20.
Емкость
перехода
при
прочих
равных
ус
-
ловиях
зависит
от
концентрации
примесей
,
или
от
удельного
со
-
противления
материала
.
Чем
больше
удельное
сопротивление
,
тем
меньше
емкость
С
пф
U
10
20
30
40
0
-5
-20 -15 -10
б
а
Рис 2.20 — Зависимость емкости ступенчатого (а)
и плавного (б) переходов от обратного напряжения
Диффузионная емкость.
При
прямом
смещении
диода
пе
-
реход
,
как
известно
,
сужается
и
соответственно
растет
барьерная
емкость
.
Однако
эта
емкость
оказывается
менее
существенной
,
чем
емкость
,
обусловленная
возрастающим
зарядом
носителей
в
базовом
слое
,
которую
называют
диффузионной
,
так
как
этот
за
-

99
ряд
лежит
в
основе
диффузии
носителей
в
базе
.
Диффузионная
емкость
С
Д
«
заряжается
»
как
инжектированными
дырками
,
так
и
электронами
,
компенсирующими
заряд
инжектированных
дырок
,
поскольку
избыточные
заряды
электронов
и
дырок
одинаковы
.
Найдем
один
из
них
,
а
именно
заряд
дырок
,
исходя
из
распреде
-
ления
(2.20):
( )
( )
(
)
0
0
1 sec
.
w
qSL p
w
Q
qS
p x dx
L
w
th
L
Δ
Δ =
Δ
=
−
⎛ ⎞
⎜ ⎟
⎝ ⎠
∫
Подставляя
сюда
( )
0
p
Δ
из
(2.20),
ток
0
I
из
(2.26
а
),
получаем
:
(
)
1 sec
.
w
Q
I
L
Δ = τ −
(2.44)
Если
поделить
этот
заряд
на
напряжение
U ,
то
интегральная
диффузионная
емкость
запишется
в
следующем
виде
:
(
)
1 sec
,
Д
Д
Q
w
С
h
L
U
R
Δ
τ
=
=
−
где
Д
U
R
I
=
—
сопротивление
диода
постоянному
току
Диффе
-
ренциальная
диффузионная
емкость
будет
иметь
аналогичную
форму
:
( )
(
)
1 sec
,
Д
Д
d
Q
w
C
h
L
dU
r
Δ
τ
=
=
−
(2.45)
где
Д
U
r
I
∂
=
∂ —
сопротивление
диода
переменному
току
.
Как
видим
,
диффузионная
емкость
(2.45)
является
функцией
прямого
тока
,
подобно
тому
,
как
барьерная
емкость
(2.43
а
)
является
функцией
обратного
напряжения
.
Кроме
того
,
диффузионная
ем
-
кость
находится
в
прямой
зависимости
от
толщины
базы
,
умень
-
шаясь
с
уменьшением
отношения
w
L
.
В
случае
толстой
базы
по
-
лучаем
:
;
Q
I
Δ ≈ τ (2.46
а
)
.
Д
Д
T
I
C
r
τ
τ
≈
=
ϕ
(2.46
б
)
100
Например
,
если
τ
= 5
мксек
,
10
I
мА
=
,
то
С
Д
=2
мкФ
.
Такие
значения
на
несколько
порядков
превосходят
величину
барьер
-
ной
емкости
.
В
случае
тонкой
базы
С
Д
приводятся
к
виду
:
;
D
Q
It
Δ ≈
(2.47
а
)
,
D
Д
Д
t
C
r
≈
(2.47
б
)
где
2
2
D
w
t
D
=
(2.48)
есть
среднее
время
диффузии
или
среднее
время
пролета
носите
-
лей
через
тонкую
базу
при
чисто
диффузионном
механизме
дви
-
жения
.
При
воздействии
импульсных
сигналов
протекают
переход
-
ные
процессы
,
которые
возникают
из
-
за
действия
зарядной
ёмко
-
сти
перехода
и
процессов
накопления
или
рассасывания
носите
-
лей
заряда
в
базовой
области
.
Удобно
рассматривать
переходные
процессы
в
диоде
в
от
-
дельности
при
отпирании
и
запирании
перехода
.
Отпирание
-
p n
перехода. Импульсное сопротивление.
Время установления прямого сопротивления
Рассмотрим
переходный
процесс
в
-
p n
переходе
при
его
отпирании
скачком
тока
.
Такой
режим
можно
обеспечить
,
выбрав
сопротивление
R
в
схеме
(
рис
. 2.21)
на
порядок
и
более
превы
-
шающим
дифференциальное
сопротивление
перехода
,
т
.
е
.
обес
-
печить
режим
генератора
тока
.
Г
Д
Г
U
U
U
I
R
R
−
=
≈
.
R
U
Г
VD
I
U
Д
Рис. 2.21 — Схема включения источника импульсного
напряжения
Г
U
при отпирании
-
p n
перехода