ВУЗ: Томский государственный университет систем управления и радиоэлектроники
Категория: Учебное пособие
Дисциплина: Электроника
Добавлен: 23.10.2018
Просмотров: 11040
Скачиваний: 27
86
U
I
1
1
R
Д
/R
Д0
R
Д
/R
Д0
r
Д
/r
Д0
r
Д
/r
Д0
R
Д0
=r
Д0
=φ
T
/I
R
Д0
=r
Д0
=φ
T
/I
а б
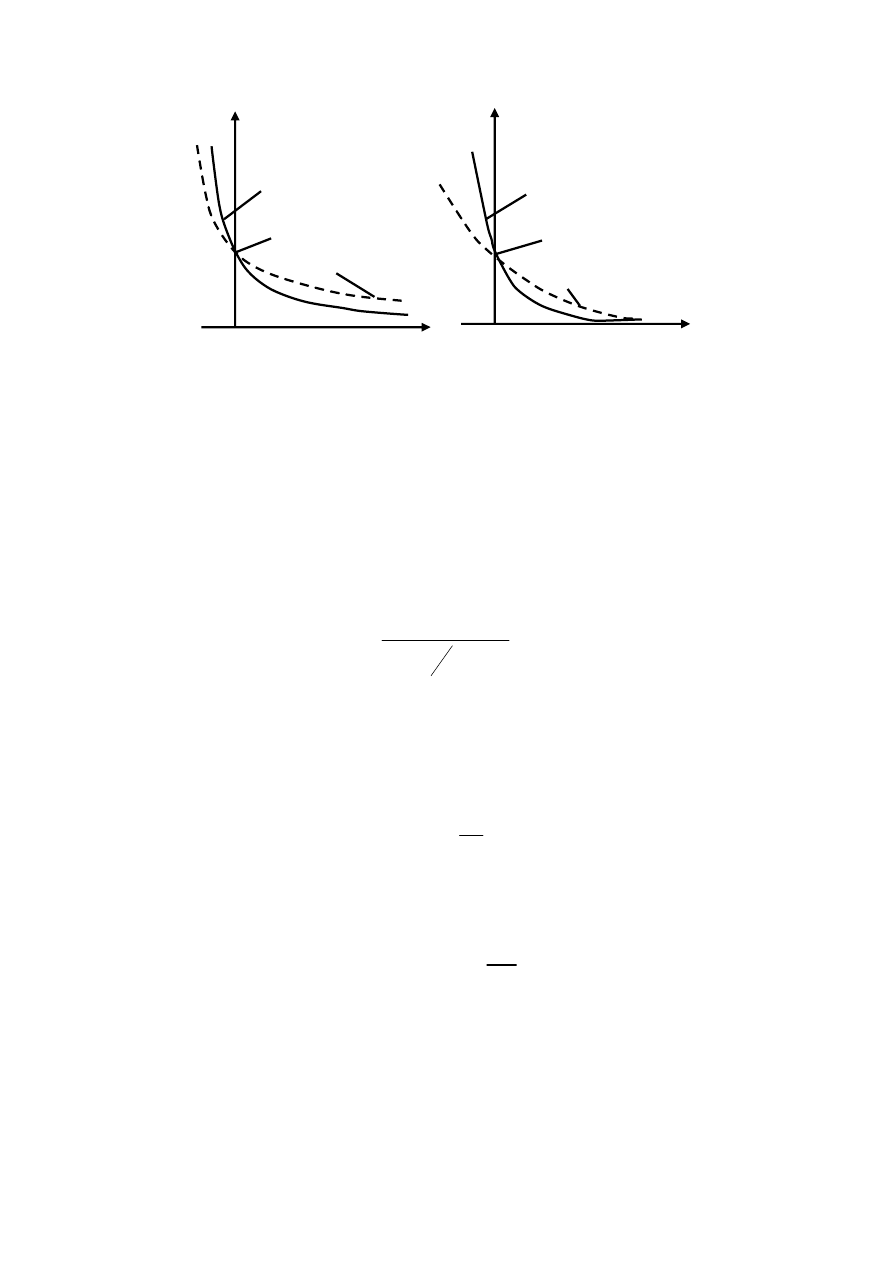
Рис. 2.14 — Зависимость сопротивлений идеализированного
диода — дифференциального сопротивления
Д
r и
д
R —
от прямого тока (а) и прямого напряжения (б)
Из
выражений
2.28
и
2.29
следует
,
что
о
дифференциальном
и
статическом
сопротивлениях
можно
говорить
только
для
кон
-
кретной
точки
вольт
-
амперной
характеристики
.
Из
формулы
(2.29
а
)
получаем
зависимость
статического
со
-
противления
от
напряжения
(
рис
. 2.14, б):
0
.
1
T
Д
U
U
R
I
e
ϕ
=
⎛
⎞
−
⎜
⎟
⎝
⎠
(2.296)
Отсюда
следует
,
что
на
обратной
ветви
характеристики
,
ко
-
гда
T
U
>> ϕ ,
сопротивление
Д
R
прямо
пропорционально
напря
-
жению
:
0
.
Д
U
R
I
=
В
нулевой
точке
0
U
=
и
0
I
=
сопротивления
Д
r
и
Д
R
,
как
нетрудно
убедиться
,
имеют
одно
и
то
же
значение
0
0
0
T
Д
Д
r
R
I
ϕ
=
=
. (2.29
в
)
Необходимо
подчеркнуть
,
что
формулы
(2.27)–(2.29)
выве
-
дены
на
основе
выражения
(2.23),
которое
не
полностью
отража
-
ет
все
свойства
реального
диода
.
Поэтому
на
практике
сопротивления
могут
значительно
от
-
личаться
от
значений
,
полученных
по
этим
формулам
.
Правиль
-

87
нее
,
видимо
,
говорить
о
характеристических
сопротивлениях
пе
-
рехода
в
диоде
и
при
необходимости
в
зависимости
от
значений
сопротивлений
нейтральных
слоев
и
выводов
вносить
поправки
.
2.5
Обратная
и
прямая
характеристики
реального
диода
Обратная характеристика реального диода
Опыт
показывает
,
что
обратный
ток
диода
не
остается
по
-
стоянным
и
равным
0
I
,
как
следует
из
формулы
(2.23).
Он
всегда
более
или
менее
сильно
растет
с
увеличением
обратного
напря
-
жения
.
Но
и
при
малых
напряжениях
обратный
ток
больше
теп
-
лового
,
особенно
у
кремниевых
диодов
,
у
которых
это
превыше
-
ние
достигает
2 — 3
порядков
.
Главные
причины
отклонения
ре
-
альной
обратной
характеристики
от
идеализированной
заключа
-
ются
:
в
термогенерации
носителей
в
области
перехода
,
поверхно
-
стных
утечках
,
а
также
в
явлениях
,
которые
при
достаточно
большом
обратном
напряжении
приводят
к
пробою
перехода
.
Таким
образом
,
обратный
ток
диода
состоит
из
нескольких
компонентов
,
из
которых
при
выводе
характеристики
(2.23)
мы
познакомились
лишь
с
одним
—
тепловым
током
.
Однако
и
этот
ток
следует
рассмотреть
подробнее
.
Тепловой ток.
Используя
в
формуле
(2.26)
соотношения
(1.16), (1.21)
и
(1.28 — 1.30),
нетрудно
представить
тепловой
ток
в
следующем
виде
:
(
)
0
2
2
,
1
T
б
i
b
I
s
b
L
=
ϕ ρ
+
ρ
где
а
p
b
μ
=
μ .
Например
,
для
германиевых
и
кремниевых
диодов
при
б
ρ =5
Ом
см
,
τ =5
мксек
и
s
=0,05
см
2
получим
( )
0 Ge
I
= 30
мкА
,
( )
0 si
I
= (3
⋅10) 10
–7
мкА
,
т
.
е
.
различие
в
токах
0
I
составляет
около
семи
порядков
.
Маленький
тепловой
ток
кремниевых
диодов
яв
-
ляется
одним
из
их
важнейших
преимуществ
,
хотя
полный
об
-
ратный
ток
реальных
кремниевых
диодов
,
как
будет
видно
ниже
,
88
значительно
больше
.
В
мощных
германиевых
диодах
с
большой
площадью
ток
0
I
может
доходить
до
нескольких
миллиампер
.
Запишем
формулу
(2.24)
в
несколько
иной
форме
.
Умножим
и
разделим
слагаемые
в
правой
части
на
соответствующие
диф
-
фузионные
длины
,
положим
( )
w
th
L
=1.
Тогда
(
)
(
)
0
0
0
.
б
Э
pб
nэ
б
Э
p
n
I
q SL
q SL
=
+
τ
τ
(2.30)
Поскольку
множители
об
б
p
τ
и
0Э
э
n
τ
есть
скорости
генера
-
ции
дырок
в
базе
и
электронов
в
эмиттере
,
выражение
(2.30)
можно
трактовать
следующим
образом
:
тепловой
ток
обусловлен
генерацией
неосновных
носителей
в
объемах
SL
,
прилегающих
к
переходу
,
откуда
эти
носители
диффундируют
в
область
потен
-
циального
барьера
и
уносятся
полем
в
другой
слой
(
рис
. 2.15).
В
равновесном
состоянии
эти
потоки
компенсируются
встречными
потоками
аналогичных
носителей
,
имеющих
достаточную
энер
-
гию
,
чтобы
преодолеть
потенциальный
барьер
.
Особый
интерес
представляет
температурная
зависимость
теплового
тока
.
Если
пренебречь
электронной
составляющей
,
то
согласно
выражению
(2.24)
тепловой
ток
зависит
от
температуры
через
параметры
:
коэффициент
диффузии
,
время
жизни
носите
-
лей
,
концентрацию
.
Из
них
главную
роль
играет
равновесная
концентрация
неосновных
носителей
0
p
.
p
n
I
0
I
0
l
Э
l l
б
переход
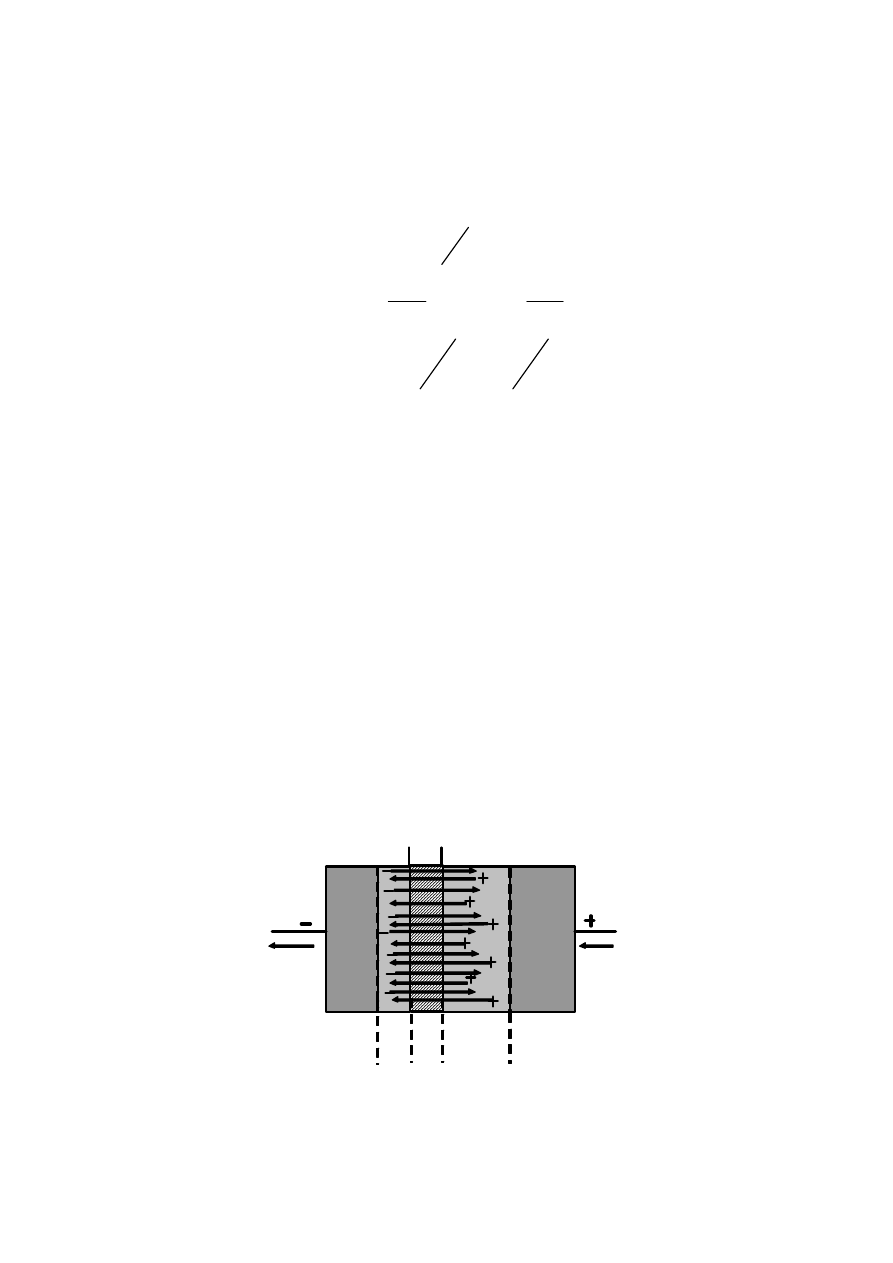
Рис. 2.15 — Происхождение электронного и дырочного
компонентов теплового тока

89
Принимая
во
внимание
выражение
(1.21
б
),
можно
сделать
заключение
,
что
тепловой
ток
пропорционален
квадрату
собст
-
венной
концентрации
полупроводника
.
Подставляя
значение
i
n
из
(1.15),
выразим
тепловой
ток
в
виде
:
( )
0
00
.
З
T
I
T
I e
−ϕ
ϕ
=
(2.31а)
Здесь ток
00
I содержит величины, мало зависящие от темпе-
ратуры. С ростом температуры примесный полупроводник по-
степенно превращается в собственный. В этом случае с учетом
(1.15) выражение для теплового тока примет вид:
( )
2
0
00
.
З
T
I
T
I e
−ϕ
ϕ
=
(2.31б)
Использовать на практике сравнительно простую зависи-
мость (2.31б) невозможно из-за сложности определения I
00
.
На практике всегда известен тепловой ток при некоторой
(обычно «комнатной») температуре
0
T , и требуется определить
его значение при другой температуре. Из формулы (2.31б) легко
получить:
( )
( )
0
1
1
2
0
0
0
.
З
T
T
I
T
e
I
T
⎛
⎞
ϕ
⎜
⎟
−
⎜
⎟
ϕ
ϕ
⎝
⎠
=
(2.32)
Учитывая, что абсолютная температура в рабочем диапазоне
меняется не очень сильно (т.е.
2
0
0
TT
T
≈
), получаем вместо (2.32)
простое приближенное соотношение
( )
( )
0
0
0
,
a T
I
T
I
T e
Δ
≈
(2.33)
где
0,13
з
a
=
ϕ ;
1
0,09
град
Ge
a
−
=
;
1
0,13
град
Si
a
−
=
.
Этими
значениями
коэффициента
а
можно
пользоваться
вплоть
до
температур
70 — 80° С для
германия
и
120 — 150° С
для
кремния
.
Несмотря
на
простоту
,
формула
(2.33)
не
всегда
удобна
для
быстрых
«
прикидок
».
Поэтому
целесообразно
заменить
степень
числа
е
степенью
числа
2.
Заменив
основание
степени
по
извест
-

90
ным
правилам
,
формулу
(2.33)
можно
представить
в
следующем
виде
0
0
20
0
10
0
0( 20
)
(
)
* 2
.
t C
t
C
I t C
I
−
=
≈
(2.34)
На
практике
весьма
распространено
правило
: «
тепловой
ток
удваивается
на
каждые
10° С
приращения
температуры
»,
что
со
-
ответствует
значению
а
= 0,07.
Из
изложенного
ясно
,
что
это
пра
-
вило
не
универсально
и
обычно
занижает
фактические
изменения
теплового
тока
в
несколько
раз
.
Главная
трудность
вычисления
теплового
тока
по
формуле
2.34
заключается
в
том
,
что
значение
теплового
тока
неизвестно
для
конкретного
экземпляра
.
Поэтому
выражением
2.34
можно
пользоваться
для
качественной
оценки
изменения
тока
диода
в
диапазоне
температур
.
Выше
отмечалось
,
что
тепловой
ток
это
только
одна
из
со
-
ставляющих
обратного
тока
.
Ток термогенерации
.
В
идеализированном
диоде
мы
счи
-
тали
переход
бесконечно
узким
и
,
следовательно
,
могли
пренеб
-
речь
генерацией
и
рекомбинацией
носителей
в
этой
области
.
Ре
-
альный
переход
имеет
конечную
ширину
,
поэтому
эти
процессы
,
имеющие
место
так
же
,
как
в
любом
другом
слое
полупроводни
-
ка
,
играют
немаловажную
роль
.
Электрическое
поле
,
которое
всегда
есть
в
переходе
,
быстро
уносит
генерируемые
носители
в
соответствующий
слой
диода
.
Это
вызывает
протекание
некото
-
рого
тока
,
который
получил
название
тока
термогенерации
G
I .
В
равновесном
состоянии
диода
этот
ток
компенсируется
равным
ему
встречным
током
—
током
рекомбинации
R
I .
Ток
рекомби
-
нации
обусловлен
теми
носителями
,
которые
непрерывно
прони
-
кают
в
переход
из
эмиттера
и
базы
,
но
не
имеют
достаточной
энергии
,
чтобы
перейти
в
смежный
слой
.
Вблизи
точки
«
отраже
-
ния
»
такие
носители
имеют
малую
скорость
и
успевают
реком
-
бинировать
.
В
неравновесном
состоянии
диода
взаимная
компен
-
сация
токов
нарушается
.
В
случае
обратного
включения
диода
превалирует
ток
термогенерации
,
так
как
высота
потенциального
барьера
увеличивается
и
проникание
носителей
в
область
пере
-
хода
с
последующей
рекомбинацией
затрудняется
.
При
величине
смещения
T
U
>> ϕ
практически
остается
только
ток
термогене
-