ВУЗ: Томский государственный университет систем управления и радиоэлектроники
Категория: Учебное пособие
Дисциплина: Электроника
Добавлен: 23.10.2018
Просмотров: 11013
Скачиваний: 27

16
Масса электрона в кристалле не совпадает с его массой m в
вакууме.
Поэтому в теории твердого тела пользуются понятием эф-
фективной массы m*, которая зависит от ряда факторов (полная
энергия, направление движения и др.). Различие между значе-
ниями m и m* может быть не только количественным, но и каче-
ственным.
Понятие дырки с точки зрения зонной теории
Предположим, что к полупроводнику приложено внешнее
напряжение. Наличие электрического поля приводит в движение
не только свободные электроны зоны проводимости, но и всю со-
вокупность электронов валентной зоны (поскольку в ней имеются
незаполненные верхние уровни, т.е. отсутствует часть электронов
с отрицательной эффективной массой). Оказывается, что движе-
ние огромного количества электронов валентной зоны с различ-
ными эффективными массами эквивалентно движению ограни-
ченного количества фиктивных частиц с положительным зарядом.
Рациональность понятия дырок состоит в том, что сложный
анализ движения электронов в почти полной валентной зоне уда-
ется свести к сравнительно простому анализу движения дырок в
почти пустой (по отношению к дыркам!) валентной зоне. При
этом поведение дырок оказывается аналогичным поведению сво-
бодных электронов в почти пустой (по отношению к электро-
нам!) зоне проводимости. Необходимо отметить, что понятие
эффективной массы допустимо по отношению к подвижным но-
сителям; его нельзя отождествлять с понятием массы в обычном
смысле этого слова. Так, различие эффективных масс не означает
различие силы тяжести.
1.4
Зонная
структура
полупроводников
При нулевой абсолютной температуре проводимость полу-
проводника, в котором отсутствуют дефекты в кристаллической
решетке (такой полупроводник называют собственным) равна
нулю, потому что зона проводимости пуста, а валентная зона за-
полнена. При любой температуре, отличной от нуля, в кристалле
появляются фононы, энергетический спектр которых непреры-
17
вен. Фононы с энергией, превышающей энергию ширины запре-
щенной зоны, переводят часть электронов из валентной зоны в
зону проводимости (рис. 1.7, а). В результате в зоне проводимо-
сти появляются свободные электроны, а в валентной зоне — не-
заполненные уровни-дырки. Те и другие образуются одновре-
менно и в равных количествах. Теперь заряды обеих зон могут
двигаться в электрическом поле, обеспечивая проводимость кри-
сталла. Перевод электрона из валентной зоны в зону проводимо-
сти аналогичен возбуждению электрона в изолированном атоме,
т.е. переводу его на один из верхних уровней. Такое возбужден-
ное состояние, как известно, является временным: через некото-
рое время электрон в атоме возвращается на исходный уровень, а
в твердом теле — в валентную зону. Возвращение электрона из
зоны проводимости в валентную зону приводит к рекомбинации
электрона и дырки. Время, в течение которого электрон находил-
ся в зоне проводимости, т.е. был свободным, называют временем
жизни. С увеличением температуры увеличивается число фоно-
нов с повышенной энергией и возрастает количество электронно-
дырочных пар.
Валентная
зона
Запре-
щенная
зона
Запре-
щенная
зона
Уровень
акцептор
Уровень
доноров
Запре-
щенная
зона
Валентная
зона
Зона
проводи-
мости
Зона
проводи-
мости
Валентная
зона
Зона
проводи-
мости
а б в
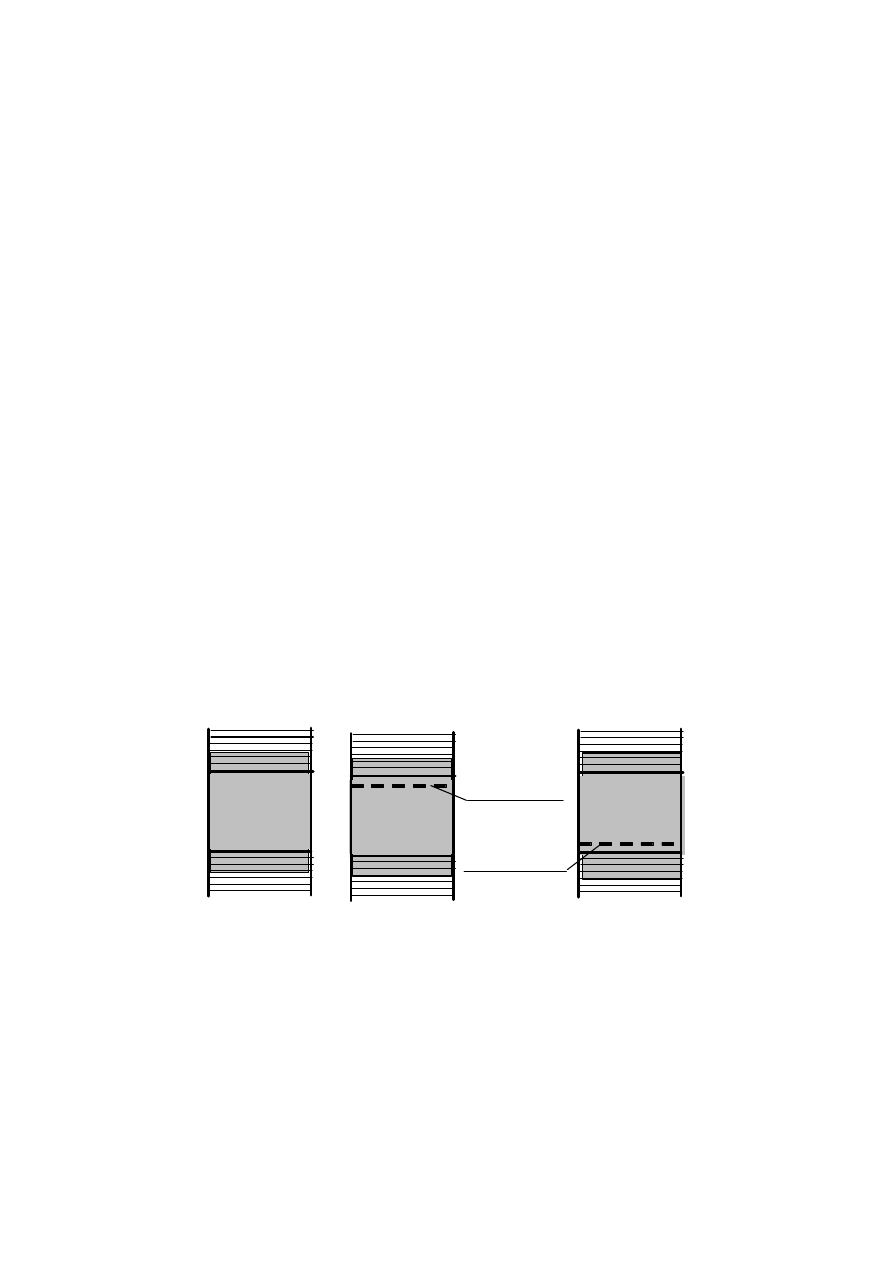
Рис. 1.7 — Зонные структуры полупроводников:
а — собственный полупроводник; б — электронный
полупроводник; в — дырочный полупроводник

18
Зонные диаграммы для примесных полупроводников пока-
заны на рис. 1.7, б и в. Обычно процентное содержание примес-
ных атомов очень мало по сравнению с атомами основного мате-
риала, а, следовательно, расстояния между ними относительно
велики. Поэтому их можно рассматривать как изолированные
атомы, уровни которых не могут образовать зоны.
Примесные уровни изображены на диаграмме штрихами;
каждый штрих соответствует атому примеси.
Донорная примесь выбирается из соображений, чтобы ее ва-
лентные уровни располагались ближе к «дну» зоны проводимо-
сти (рис. 1.7, б); все эти уровни заполнены при температуре абсо-
лютного нуля. Акцепторная примесь выбирается из соображений,
чтобы ее валентные уровни располагались ближе к «потолку» ва-
лентной зоны (рис. 1.7, в); все эти уровни пусты при температуре
абсолютного нуля. Переходы электронов с донорного уровня в
зону проводимости, а из валентной зоны на акцепторный уровень
требуют сравнительно небольшой энергии. Поэтому при нагреве
число фононов, способных ионизировать донор или акцептор и
тем самым создать свободный электрон или свободную дырку,
будет гораздо больше числа фононов, способных перевести элек-
трон через всю запрещенную зону и образовать электронно-
дырочную пару.
Соответственно, проводимость, обусловленная приме-
сями, оказывается гораздо больше собственной. Однако этот
вывод справедлив только до некоторой температуры. Дело в
том, что по мере повышения температуры собственная про-
водимость растет непрерывно, а примесная имеет предел, со-
ответствующий ионизации всех наличных примесных ато-
мов. С повышением температуры увеличивается собственная
концентрация электронов и дырок, а следовательно, увели-
чивается и собственная проводимость полупроводника. При
высоких температурах проводимость всегда является собст-
венной. Критерий вырождения примесного полупроводника в
собственный будет рассмотрен позже.
Увеличение концентрации примесей приводит к уменьше-
нию расстояния между примесными атомами, и их энергетиче-
ские уровни постепенно превращаются в зоны. Образовавшаяся
примесная зона, расширяясь, в конце концов сливается с бли-
19
жайшей разрешенной.
Обычно в полупроводниках одновременно присутствуют
донорная и акцепторная примеси, рис. 1.8, но чаще — в разных
концентрациях (
Д
а
N
N
>
или
a
Д
N
N
>
).
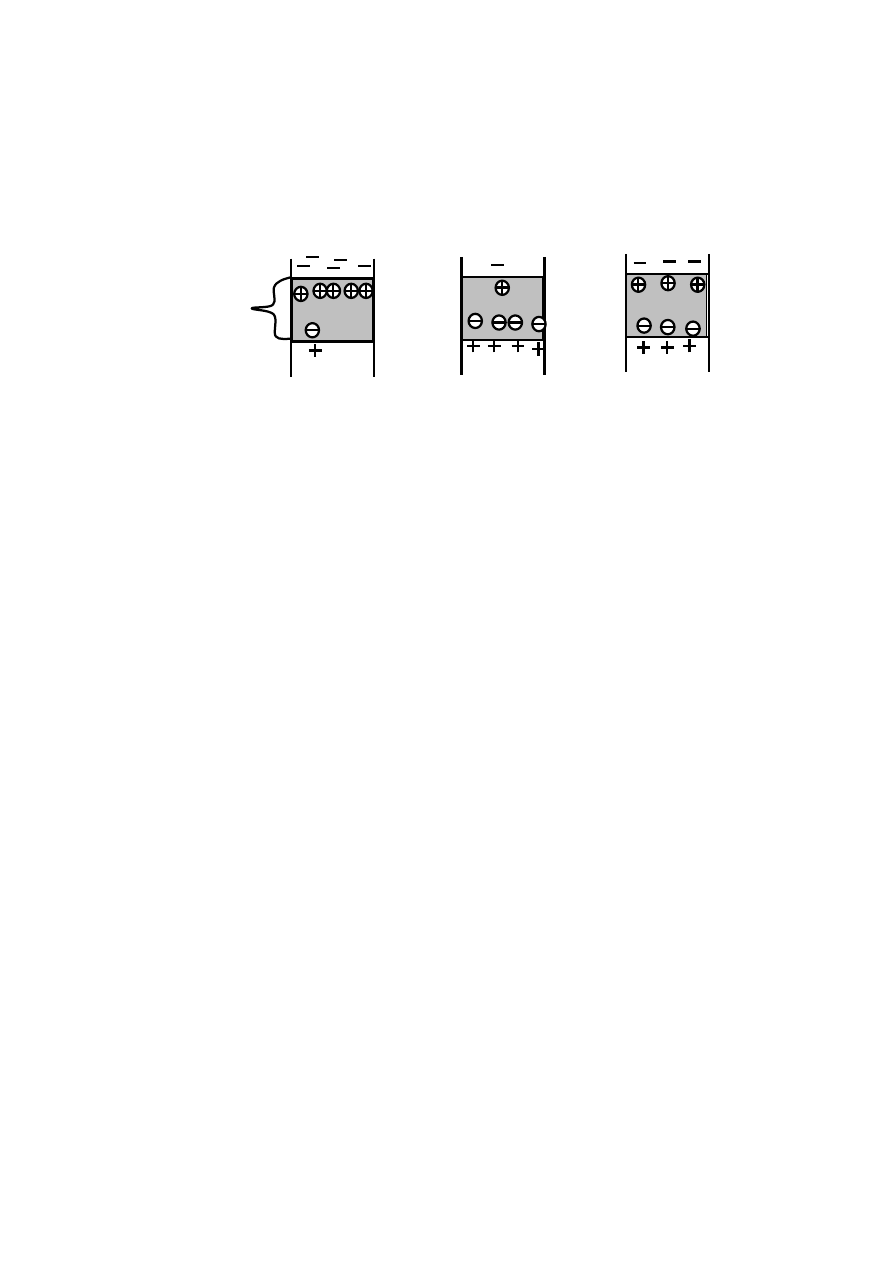
Рис. 1.8. Диаграммы энергетических уровней при различных
концентрациях донорных и акцепторных атомов для Т=0 К°.
а — превалирует донорная примесь; б — превалирует акцепторная
примесь; в — количество обеих примесей одинаково
Рассматривая этот случай, следует учесть, что при нулевой
температуре система должна обладать минимальной энергией.
Пусть
Д
a
N
N
>
, тогда при нулевой температуре (здесь и в
дальнейшем будем иметь в виду абсолютный ноль) все акцептор-
ные уровни заполнятся электронами, и число заполненных до-
норных уровней уменьшится.
При повышении температуры с донорных уровней будет
происходить переход электронов в зону проводимости основного
полупроводника, так как для перехода электронов с акцепторных
уровней требуется гораздо больше энергии.
В дальнейшем под
Д
N и
a
N будем понимать эффективные
концентрации. Если количество обоих типов примеси одинаково
(
Д
а
N
N
=
), то эффективные концентрации доноров и акцепторов
равны нулю. Такой полупроводник называется компенсирован-
ным. Он имеет такую же удельную проводимость, как и собст-
венный, но отличается от последнего (по времени жизни носите-
лей и некоторым другим параметрам), поскольку наличие значи-
тельного количества примесей нарушает однородность кристал-
лической решетки.
За
прещ
енна
я
зона
а
б
в

20
1.5
Концентрации
носителей
в
зонах
полупроводника
Проведем анализ полупроводниковых материалов с тем,
чтобы получить качественные и количественные оценки для кон-
центраций электронов и дырок в зависимости от концентраций
примесей, изменений температуры и некоторых других внешних
воздействий, т.к. величины концентраций свободных электронов
и дырок определяют удельную проводимость полупроводника, а
следовательно, его электрические свойства.
В теории твердого тела доказано, что энергетические уровни
распределены по высоте разрешенной зоны неравномерно: плот-
ность их меняется от границы в глубь зоны. Таким образом, каж-
дому уровню с энергией W соответствует определенная плот-
ность
( )
P W , т.е. число уровней, отнесенное к единице энергии и
единице объема материала. Вблизи «дна» и «потолка» разрешен-
ных зон плотность уровней для узких интервалов энергии можно
выразить формулой:
( )
3
*
2
2
3
2
2
уровней
.
дж*см
гр
m
P W
W
W
h
⎛
⎞
⎛
⎞
π
=
−
⎜
⎟
⎜
⎟
π
⎝
⎠
⎝
⎠
(1.1а)
Здесь h — постоянная Планка; m* — эффективная масса;
W — энергия, которая отсчитывается от граничного уровня
внутрь разрешенных зон.
Вероятность нахождения электрона или дырки на том или
ином уровне в зависимости от их энергии описывается распреде-
лением Ферми-Дирака:
( )
1
1
F
W W
kT
F W
e
−
=
+
, (1.1б)
где
k
— постоянная Больцмана; Т
—
абсолютная температура;
F
W
— энергия, называемая уровнем Ферми. С формальной точки
зрения энергия
F
W
соответствует такому энергетическому уров-
ню, вероятность заполнения которого электронами или дыр-
ками равна 0.5.
В статистической физике энергию принято выражать не в
джоулях, а в электрон-вольтах или просто в вольтах (численно