ВУЗ: Томский государственный университет систем управления и радиоэлектроники
Категория: Учебное пособие
Дисциплина: Электроника
Добавлен: 23.10.2018
Просмотров: 11015
Скачиваний: 27

21
эти величины одинаковы). Чтобы перейти от одной размерности
к другой, достаточно разделить энергии
W
и
kT
на элементар-
ный заряд.
Сделав такую замену в формулах (1.1), получим:
( )
3
*
2
2
3
2
2
уровней
;
В*см
гр
qm
P
h
⎛
⎞
π
⎛
⎞
ϕ =
ϕ − ϕ
⎜
⎟
⎜
⎟
π
⎝
⎠
⎝
⎠
(1.2а)
( )
1
,
1
n
F
T
F
e
ϕ =
ϕ − ϕ
+
ϕ
(1.2
б
)
где
ϕ —
потенциал
,
характеризующий
энергию
уровня
;
F
ϕ
—
уровень Ферми (потенциал Ферми)
в вольтах;
T
ϕ
—
температурный потенциал
.
T
kT
q
ϕ =
(1.3)
Название
«
температурный
потенциал
»
для
величины
T
ϕ
вполне
оправдано
,
в
силу
значительной
зависимости
от
темпера
-
туры
.
Полезно
запомнить
значение
T
ϕ ,
при
температуре
Т
=300°
К
(
которую
принято
называть
«
комнатной
»)
равен
(
)
0
300 K
25
мВ
.
T
ϕ
=
На
зонной
диаграмме
(
рис
. 1.9)
функции
( )
P
ϕ
и
( )
n
F
ϕ
по
-
казаны
для
собственного
полупроводника
.
Дальнейшие
выводы
будут
справедливы
и
по
отношению
к
примесным
полупроводни
-
кам
.
В невырожденных полупроводниках уровень Ферми
F
ϕ
всегда лежит в запрещенной зоне.
Понятие
невырожденный
полупроводник
рассмотрим
позже
.
Глубину
залегания
уровня
Ферми
можно
характеризовать
«
расстоянием
»
от
одной
из
раз
-
решенных
зон
,
выраженным
в
единицах
температурного
потен
-
циала
.
Для
невырожденных
полупроводников
чаще
соблюдаются
неравенства
:
;
с
F
T
ϕ − ϕ >> ϕ (1.4
а
)
F
V
T
ϕ − ϕ >> ϕ , (1.4
б
)
22
где
c
ϕ
и
V
ϕ
—
потенциалы
«
дна
»
зоны
проводимости
и
«
потол
-
ка
»
валентной
зоны
соответственно
.
С физической точки зрения температурный потенциал
есть выраженная в электрических единицах статистическая
температура или близкая к ней средняя кинетическая энер-
гия свободного электрона в электронном газе
.
При
температуре
Т
=
0°
К
функция
( )
F
ϕ (
рис
. 1.9)
имеет
сту
-
пенчатый
характер
,
это
соответствует
уже
известным
фактам
:
ва
-
лентная
зона
полностью
заполнена
(
1
Fn
= ),
зона
проводимости
пуста
(
0
n
F
=
). При температуре
0
0
T
≠
К ступенька функции
( )
F
ϕ
сглаживается и получается конечная (хотя и крайне малая)
вероятность нахождения электронов в зоне проводимости.
Одновременно вероятность нахождения электронов в ва-
лентной зоне делается меньше единицы. В последнем случае
удобнее пользоваться вероятностью отсутствия электронов на
уровнях или, что то же самое, вероятностью наличия дырок. Из
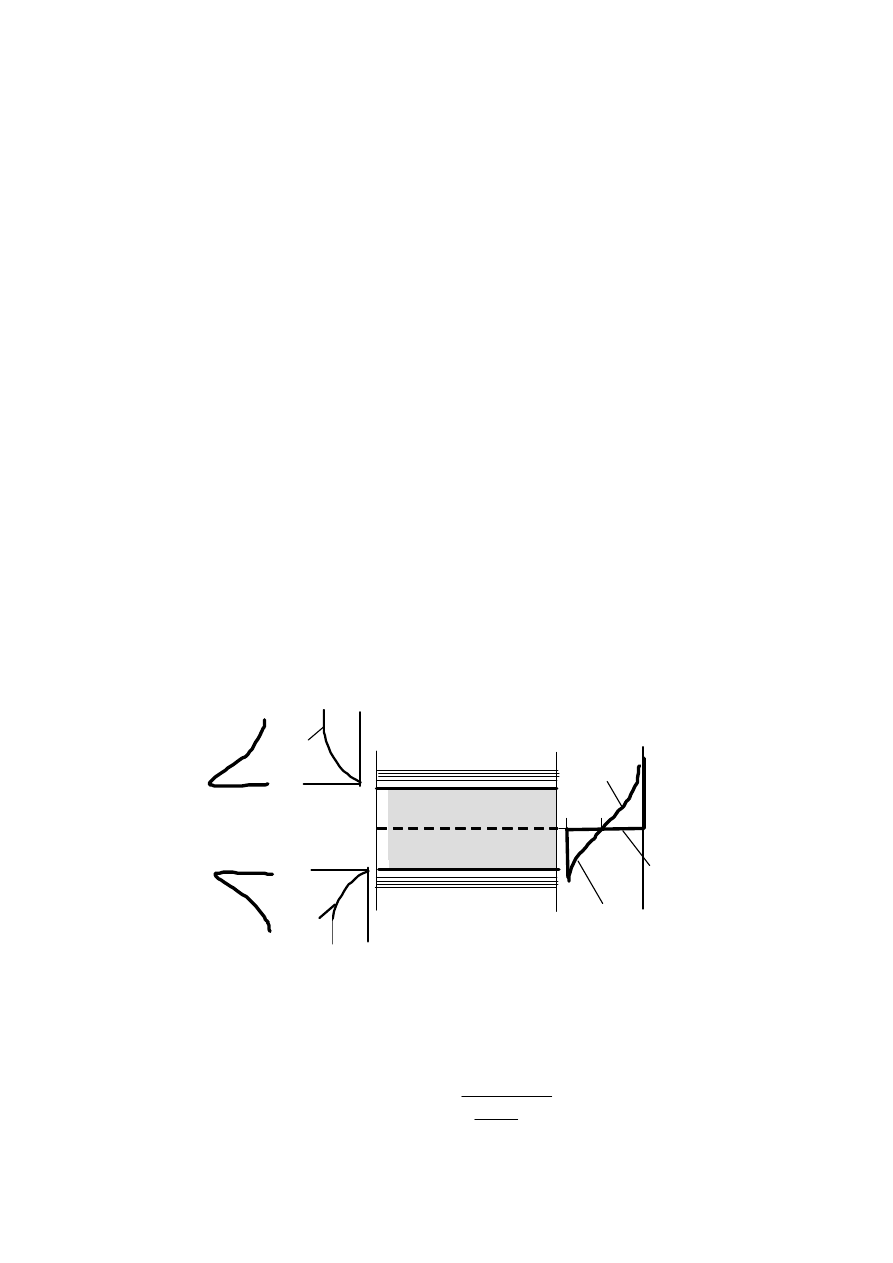
рис. 1.9 следует, что максимальные концентрации электронов в
зоне проводимости и дырок в валентной зоне имеют место на
границах зон. Плотность состояний на границах зон равна нулю и
увеличивается в глубь разрешенных зон.
1
0,5
ϕ
V
ϕ
C
n
P
P
n
(ϕ
)
T
≠0
T=0
ϕ
F
Запрещенная
зона
Валентная зона
Зона проводимости
F
n
(ϕ
)
P
p
(ϕ
)
Рис. 1.9 — Плотность уровней энергии, функция вероятности
и концентрация носителей в собственном полупроводнике
1
1
.
1
F
T
p
n
F
F
e
ϕ −ϕ
ϕ
= −
=
+
(1.5)

23
Учитывая неравенство (1.4а), можно записать:
.
F
T
n
F
e
ϕ−ϕ
−
ϕ
=
(1.6
а
)
Аналогично
,
учитывая
неравенство
(1.4
б
),
убеждаемся
,
что
и
в
валентной
зоне
,
где
0
F
ϕ−ϕ <
,
экспонента
в
выражении
(1.5)
много
больше
единицы
.
F
T
p
F
e
ϕ −ϕ
−
ϕ
≈
(1.6
б
)
Функции
(1.6),
которые
являются
частным
случаем
распре
-
деления
Ферми
-
Дирака
(
для
области
энергий
,
значительно
пре
-
вышающих
F
ϕ
),
называются
распределением
Максвелла
–
Больц
-
мана
.
Это распределение представляет собой основу теории
полупроводников
,
т.к. при этом существенно упрощается ко-
личественный анализ полупроводниковых материалов и
приборов на их основе.
Концентрация
свободных
электронов
в
зоне
проводимости
с
учетом
проведенного
выше
анализа
запишется
в
виде
:
2
(
)
( )
c
c
n
n
P
F
d
∞
ϕ
=
ϕ − ϕ
ϕ ϕ
∫
,
где подынтегральное выражение есть количество заполненных
уровней в элементарном интервале энергии, а множитель 2 озна-
чает, что на каждом уровне могут (по принципу Паули) нахо-
диться два электрона. Подставив (1.2а) и (1.6а) под знак интегра-
ла, после преобразований получим:
3
2
2
;
2
2(
)
,
c
F
T
c
n
T
n
N e
m q
Nc
h
ϕ −ϕ
−
ϕ
=
π
ϕ
=
(1.7а)
где
c
N — эффективная плотность состояний (в 1 см
3
) в зоне про-
водимости. Из (1.7а) следует, что
c
N есть максимально воз-
можная концентрация электронов в невырожденном полу-
проводнике.
Концентрация свободных дырок в валентной зоне определя-
ется выражением:

24
2
[ (
)]
( )(
).
v
V
p
p
P
F
d
−∞
ϕ
=
− ϕ − ϕ
ϕ − ϕ
∫
Подставив (1.2а) и (1.6б), после преобразований получим:
3
2
2
;
2
2(
)
,
F
V
T
V
p
T
V
p
N e
m q
N
h
ϕ −ϕ
−
ϕ
=
π
ϕ
=
(1.7б)
где
v
N — эффективная плотность состояний в валентной зоне.
Легко убедиться, что произведение концентраций np не за-
висит от положения уровня Ферми и определяется только темпе-
ратурой и шириной запрещенной зоны:
,
З
T
C
V
np
N N e
ϕ
−
ϕ
=
(1.8)
где
з
с
v
ϕ = ϕ − ϕ
— ширина запрещенной зоны.
Из выражения (1.8) следует, учитывая, что эффективные
плотности состояний относительно слабо зависят от типа полу-
проводникового материала при постоянной температуре, произ-
ведение концентраций зависит в основном от ширины запрещен-
ной зоны, т.е. характеристики полупроводника. Для кремния ши-
рина запрещенной зоны примерно в два раза больше чем у герма-
ния, в результате чего произведение концентраций электронов —
дырок у кремния на три порядка меньше. Следовательно, элек-
трические параметры и характеристики кремния и германия
должны существенно отличаться.
Из формул (1.7) отношение концентраций получается в сле-
дующем виде:
2(
)
;
,
2
E
F
T
C
V
c
v
E
N
n
e
p
N
ϕ −ϕ
−
ϕ
=
ϕ + ϕ
ϕ =
(1.9
а
)
где
E
ϕ
—
потенциал
середины
запрещенной
зоны
,
который
ино
-
гда
называют
электростатическим
потенциалом
полупроводника
.
Если
принять
,
что
выполняется
условие
c
v
N
N
=
,
выражение
(1.9
а
),
можно
записать
в
виде
:

25
2(
)
.
E
F
T
n
e
p
ϕ −ϕ
−
ϕ
=
(1.9
б
)
Анализируя
выражение
(1.9
а
),
можно
сделать
следующие
выводы
:
1.
Если
уровень
Ферми
совпадает
с
электростатическим
по
-
тенциалом
,
тогда
1
n
p
= , т.е. полупроводник является собствен-
ным.
2. При выполнении условия
F
E
ϕ > ϕ
1
n
p
> , т.е. полупро-
водник электронный.
3. При выполнении условия
F
E
ϕ < ϕ
1
n
p
< , т.е. полупро-
водник дырочный.
4. Из выражения (1.9б) следует, что изменение уровня Фер-
ми должно приводить к изменению концентрации примесей. Фи-
зически можно изменять концентрацию электронов или дырок,
вводя разное количество примесей в основной полупроводник, а
уровень Ферми рассчитывать.
1.6
Уровень
Ферми
При анализах, которые мы провели выше, считалось, что
уровень Ферми нам известен, и с его помощью вычислялись кон-
центрации свободных носителей заряда. На самом же деле уро-
вень Ферми является функцией этих концентраций, так как изме-
нить уровень Ферми можно только, изменив концентрацию доно-
ров или акцепторов, а концентрации носителей оценить из тех
или иных соображений или условий.
Используя выражения (1.2б) и (1.5), интегралы легко при-
вести к виду
(
)
0
2
,
1
T
d
e
∞
χ
η−
ϕ
η η
= ν
τ
+
∫
(1.10)
где
в
случае
электронного
и
дырочного
полупроводников
соот
-
ветственно
запишем
: