ВУЗ: Томский государственный университет систем управления и радиоэлектроники
Категория: Учебное пособие
Дисциплина: Ядерная физика
Добавлен: 23.10.2018
Просмотров: 3818
Скачиваний: 10
46
Глава 4. Элементарные частицы
1936 г. — К. Андерсен и Неддермайер открыли в космических лучах мюон (
µ),
тяжелый аналог электрона.
1947 г. — С. Пауэлл (1903–1969 гг.) совместно с Дж. Оккиалини (1907–1993 гг.)
и Ч. Латтесом (1924–2005 гг.) в космических лучах открыли заряженный пион (
π
+
,
π
−
).
1950 г. — С. Пауэлл и Дж. Оккиалини открыли нейтральный пион (
π
0
).
1953 г. — Ф. Рейнес (1918–1998 гг.) совместно с К. Коуэнном открыли экспери-
ментально антинейтрино (˜v
e
).
1956 г. — они же открыли электронное нейтрино (v
e
).
1953 г. — открыт сигма-плюс-гиперон (
Σ
+
).
1954 г. — открыт сигма-минус-гиперон (
Σ
−
).
1955 г. — антипротон — первая тяжелая античастица.
1956 г. — антинейтрон.
1962 г — мюонное нейтрино (v
µ
).
1974 г. — J
/Ψ — частицы, первые из семейства очарованных.
1981 г. — красивые частицы.
1982–1983 гг. — W
+
, W
−
, W
0
-бозоны, переносчики слабого взаимодействия и т. д.
К середине 80-х годов было открыто около
≅ 380 элементарных частиц, причем
≈ 350 из них — так называемые резонансы.
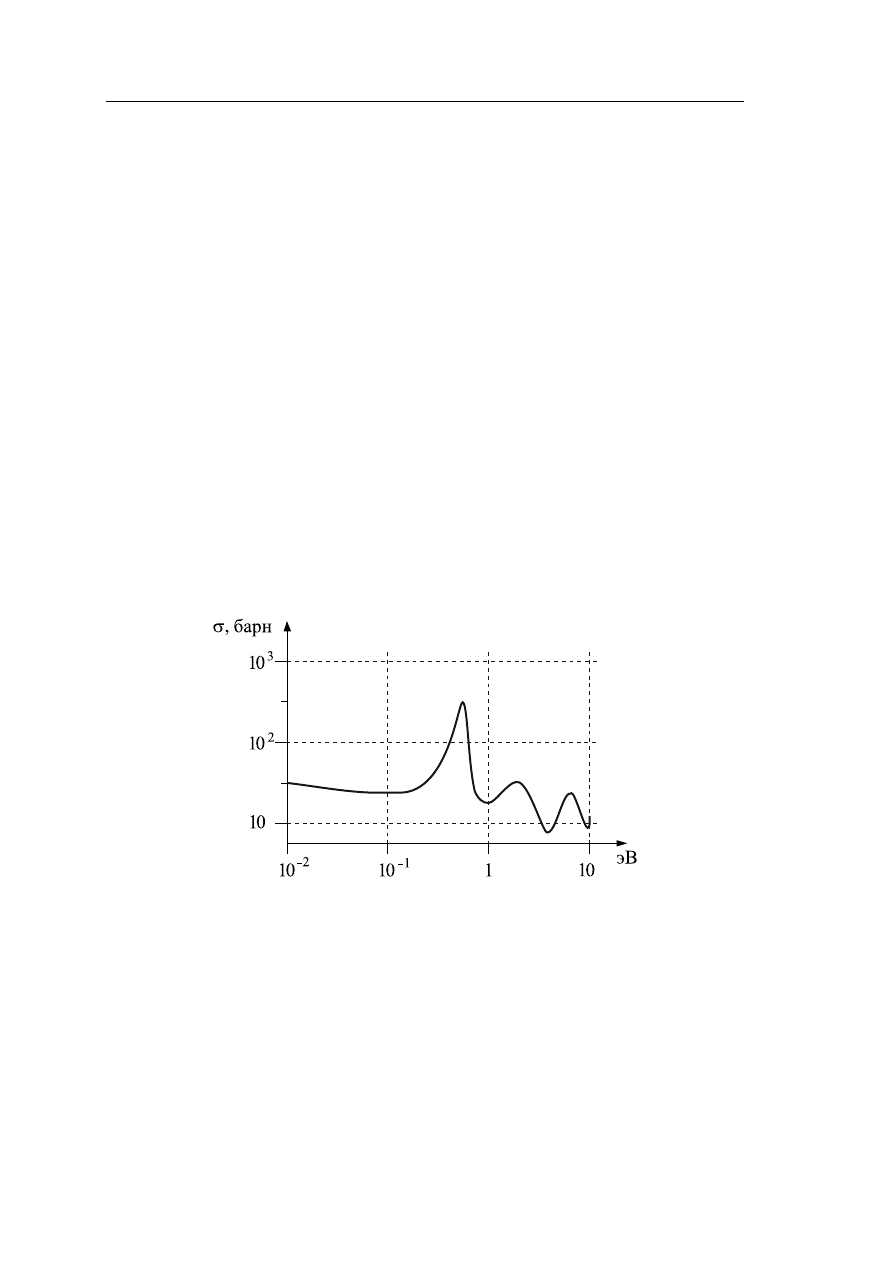
На рисунке 4.1 показана кривая зависимости эффективного сечения взаимо-
действия тепловых нейтронов с ядрами серебра.
Рис. 4.1 – Зависимость эффективного сечения взаимодействия нейтронов
с ядрами серебра (естественная смесь изотопов) от энергии нейтронов
Отчетливо видны резонансные пики взаимодействия с различными изотопами
ядер серебра. Каждый изотоп — частица другого сорта (другая масса) — поэтому
каждый такой резонанс рассматривался как частица, а сами частицы получили
название резонансов.

4.2 Свойства и типы элементарных частиц
47
4.2 Свойства и типы элементарных частиц
В силу малых размеров и масс элементарные частицы подчинены квантовым
законам. Наиболее важное квантовое свойство всех элементарных частиц — спо-
собность рождаться и уничтожаться при взаимодействии с другими элементарны-
ми частицами. В этом отношении они полностью аналогичны фотонам: в атоме
нет фотона, как составной части атома, но тем не менее атомы излучают фотоны.
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Универсальным свойством элементарных частиц является суще-
ствование античастиц.
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Античастица отличается от частицы только знаком величины, имеющей смысл
заряда. Зарядовой является величина, которая отвечает за силу взаимодействия
с другими частицами: масса — в гравитационных взаимодействиях, электрический
заряд — при электромагнитных взаимодействиях, странность — при взаимодейст-
вии странных частиц и т. д. Частицы, у которых эти величины равны нулю, тож-
дественны своим античастицам и поэтому называются истинно нейтральными.
Истинная нейтральность — более глубокое свойство, чем электрическая нейтраль-
ность. Например, нейтрон, у которого барионный заряд B
= 1 не является истинно
нейтральной частицей. К истинно нейтральным частицам относятся фотон,
π
0
—
нейтральный пион,
η
0
— мезон, J
/Ψ — мезон, Y — ипсилон-частица.
Так как каждая пара частица-античастица образуют истинно нейтральную си-
стему, то эта пара может превратиться (и превращается) в другую истинно ней-
тральную систему, если только эти превращения не запрещены другими «незаря-
довыми» законами сохранения. В частности, при столкновении частицы и анти-
частицы обе могут исчезнуть и превратиться в фотоны. Такой процесс называют
аннигиляцией.
e
+
+ e
−
→ γ + γ.
Процесс, обратный аннигиляции, называется рождением пар.
Установлено четыре типа фундаментальных взаимодействий. Они отличают-
ся интенсивностью процессов, которые они вызывают среди ЭЧ. Интенсивность,
в свою очередь, зависит от энергии взаимодействующих частиц. В таблице 4.1
показано, какую долю от сильного взаимодействия, принятого за единицу, состав-
ляют интенсивности других взаимодействий при двух значениях энергии частиц.
Таблица 4.1 – Сравнительная характеристика взаимодействий
Энергия
Сильное
Электро-
магнитное
Слабое
Гравита-
ционное
100 МэВ
1
10
−2
10
−14
10
−39
1 ГэВ
1
10
−2
10
−10
10
−38
радиус действия
∼ 10
−15
м
∞
< 10
−17
м
∞
Общим свойством всех фундаментальных взаимодействий является их способ-
ность вызывать распады частиц (может, кроме гравитационного). Стабильны толь-
ко электрон, протон, нейтрино. Резонансы распадаются только за счет сильного
взаимодействия за время
τ > 10
−14
с (нейтрон распадается за
∼ 10
3
c).

48
Глава 4. Элементарные частицы
По видам взаимодействий, в которых они участвуют, и величине спина все
элементарные частицы делятся на три группы.
I. Переносчики взаимодействий. Фотоны — переносчики электромагнитных
взаимодействий, W
+
, W
−
, Z
0
-бозоны, переносчики слабых взаимодействий. Все
переносчики имеют целочисленный спин: S
= 1. У гипотетических переносчиков
гравитационного взаимодействия — гравитонов — S
= 2.
II. Лептоны: e
−
,
µ
−
,
τ
−
, v
e
, v
µ
, v
τ
и их античастицы (
τ — таон, v
τ
— таонное
нейтрино). У всех S
= 1/2 (все — фермионы). Они участвуют в слабых и электро-
магнитных взаимодействиях. Все лептоны на современном уровне знания можно
назвать истинно элементарными частицами, так как у них пока не обнаружена
внутренняя структура.
III. Адроны участвуют во всех взаимодействиях, в том числе и сильных (ад-
рон — сильный). По величине спина адроны делятся на две группы. Мезоны (S
=
= 0, 1, 2, . . .), сюда относятся π
+
,
π
−
,
π
0
, k
+
, k
−
и т. д. Барионы (S
= 1/2) — нуклоны,
гипероны и т. д. Протон — единственный стабильный барион.
4.3 Реакции взаимодействия элементарных частиц
В реакциях между элементарными частицами, как нигде, проявляется связь
между энергией и массой. Наблюдается сколько угодно реакций, когда сумма масс
продуктов реакции много больше (в десятки и сотни раз) суммы масс до реакции:
∑ m
′
i
≫ ∑ m
i
. Найдем минимальное значение кинетической энергии (E
пop
) нале-
тающей частицы, при которой возможна эндотермическая реакция. Поскольку E
k
должна быть большой, то следует рассматривать релятивистcкий случай.
Доказательство. Введем обозначения: m
1
— масса налетающей частицы, m
2
—
масса частицы-мишени, m
′
i
— массы образовавшихся после реакции частиц. В ла-
бораторной (неподвижной) системе координат законы сохранения импульса и энергии:
P
1
= P
′
1
+ P
′
2
+ P
′
3
+ . . .
E
1
+ m
2
c
2
= E
′
1
+ E
′
2
+ E
′
3
+,
где E
1
, E
′
1
, E
′
2
, E
′
3
— полные энергии частиц.
В этой системе координат слишком много неизвестных. Воспользуемся следу-
ющим обстоятельством: в теории относительности доказывается, что
(∑ E
i
)
2
− (∑ P
i
⋅ c)
2
= (∑ E
0
)
2
,
где E
0
— энергия покоя, являющаяся инвариантом в любой системе координат, т. е.
(∑ E
i
)
2
− (∑ P
i
⋅ c)
2
= inυ.
(4.1)
В нашем случае:
(E
1
+ m
2
c
2
)
2
− P
2
1
c
2
= (∑ m
′
i
)
2
⋅ c
4
,
(4.2)
левая половина равенства записана в лабораторной системе координат, правая —
в системе центра инерции, где частицы покоятся относительно друг друга.

4.4 Характеристика взаимодействий элементарных частиц
49
Учтем, что E
1
= c ⋅
√
P
2
1
+ m
2
1
⋅ c
2
, откуда
E
2
1
= c
2
⋅ P
2
1
+ m
2
1
c
4
⇒ P
2
1
⋅ c
2
= E
2
1
− m
2
1
⋅ c
4
⇒ (4.2);
E
2
1
+ m
2
2
c
4
+ 2m
2
c
2
E
1
− E
2
1
+ m
2
1
c
4
= (∑ m
′
i
)
2
⋅ c
4
∣
1
c
2
∣ .
Полная энергия E
1
= E
1k
+ m
1
⋅ c
2
, учтем и это:
2m
2
(E
1k
+ m
1
⋅ c
2
) = (∑ m
′
i
)
2
⋅ c
2
− m
2
1
⋅ c
2
− m
2
2
⋅ c
2
;
2m
2
⋅ E
1k
= (∑ m
′
i
)
2
⋅ c
2
− c
2
⋅ (m
2
1
+ m
2
2
+ 2m
1
m
2
) ;
(m
2
1
+ m
2
2
+ 2m
1
m
2
) = (m
1
+ m
2
)
2
.
Учтем, что E
1k
= E
пop
.
Окончательно:
E
пop
= c
2
(∑ m
i
)
2
− (m
1
+ m
2
)
2
2m
2
.
(4.3)
В числителе разность квадратов масс покоя частиц после реакции и до реакции.
4.4 Характеристика взаимодействий элементарных
частиц
4.4.1 Гравитационное взаимодействие
Это абсолютно универсальное взаимодействие (ему подчиняются даже части-
цы, не имеющие массы покоя (например, фотон)), но в мире элементарных частиц
очень слабое. Предполагается, что при r
∼ 10
−35
м (планковский радиус) гравита-
ционное взаимодействие сравняется с другими — все виды взаимодействия ниве-
лируются.
4.4.2 Электромагнитное взаимодействие
С классической точки зрения (теории Максвелла) электромагнитное взаимо-
действие осуществляется через электромагнитное поле. Квантовая электродина-
мика (самая точная теория на сегодняшний день) «стоит» на том, что переносчи-
ком любого взаимодействия является частица. Переносчиком электромагнитного
взаимодействия является фотон. Поскольку фотон — безмассовая частица, радиус
электромагнитного взаимодействия бесконечен (теоретически). Экспериментально
проверена сфера действия от 10
−17
до 10
8
м (больше 100 км никто не проверял, но
нет никаких оснований не считать, что сфера действия электромагнитного взаи-
модействия равна размеру Вселенной). Из-за дальнодействия эти силы во многих
случаях оказываются главными даже в ядерных процессах. Например, осколки де-
ления ядер разлетаются именно под действием электромагнитных сил.
Электромагнитные взаимодействия — это все электрические и магнитные явле-
ния, все оптические, химические и тепловые явления. Тем не менее в характере

50
Глава 4. Элементарные частицы
электромагнитных взаимодействий есть ограничения. Не все системы являются
электрически заряженными, так как есть положительные и отрицательные заря-
ды, компенсирующие друг друга. А радиус взаимодействия нейтральных систем
конечен (например, Ван-дер-Ваальсовы силы). Нейтральные частицы со спином
(например, нейтроны) взаимодействуют только через магнитное поле, а оно зна-
чительно слабее электрического. Еще слабее силы электромагнитного взаимодей-
ствия между нейтральными и безспиновыми частицами (например, между ней-
тральными пионами,
π
0
).
4.4.3 Сильное взаимодействие
Сильному взаимодействию подвержены адроны, которые подразделяются на
две группы: барионы — частицы с полуцелым спином и мезоны — частицы с це-
лым спином. Все адроны, кроме протона, нестабильны и распадаются на другие
частицы:
n
→ p + e
−
+ ˜v
e
,
π
+
→ µ
+
+ v
µ
и т. д.
Барионы никогда не распадаются только на мезоны и лептоны. Чтобы охватить
всю совокупность возможных распадов и «запретить» ненаблюдаемые, но возмож-
ные с точки зрения законов сохранения энергии, импульса, момента импульса,
электрического заряда, вводится специальное квантовое число — барионный заряд
(B). Считается, что B
= 1 для бариона и B = −1 для антибариона. Для всех мезо-
нов, лептонов и переносчиков взаимодействий B
= 0. Во всех реакциях с участием
любых элементарных частиц выполняется закон сохранения барионного заряда:
алгебраическая сумма барионов равна const. Из этого закона следует, что рож-
дение бариона должно сопровождаться рождением антибариона. Протон — самый
легкий из барионов, поэтому он стабилен. (Экспериментально установлено, что
время жизни протона
τ > 10
32
лет.)
Сильное взаимодействие подчиняется еще ряду законов, которые не выполня-
ются для других взаимодействий. К их числу относится закон сохранения изото-
пического спина (понятие было введено В. Гейзенбергом в 1932 г.). Оказывается,
что все адроны разбиваются на группы. В каждую группу входят частицы пример-
но с равными массами и совершенно одинаковыми внутренними характеристиками
(спином и т. д.), но с разными электромагнитными свойствами (электрическими за-
рядами, магнитными моментами). Частицы из одной группы участвуют в сильных
взаимодействиях одинаково, т. е. независимо от электрического заряда и магнит-
ного момента. Эта независимость является физической симметрией, получившей
название изотопической (или зарядовой) независимости сильных взаимодействий.
Группы из одинаковых по отношению к сильному взаимодействию частиц на-
зываются изотопическими мультиплетами. Объединение частиц в такие группы
осуществляется с помощью изотопического спина (собственного изотопическо-
го момента). Формально эта величина не отличается от обычного спина, кото-
рый характеризует электромагнитное взаимодействие. Изотопический спин так-
же задается одним целым (или полуцелым) числом постоянных Планка (
~): T =
= 0, 1/2, 1, 3/2, . . . (частиц с T > 3/2 пока не обнаружено).
Число адронов в мультиплете, как и число проекций для обычного спина, 2T
+1
(сравните: 2l
+ 1). Изотопический дублет p и n: T = 1/2; проекция на ось «z»