ВУЗ: Алтайский Государственный Университет
Категория: Учебное пособие
Дисциплина: Аналитические методы в экономике
Добавлен: 23.10.2018
Просмотров: 374
Скачиваний: 7
Раздел 3. Математические и инструментальные методы портфельного анализа
Портфельный анализ. Модель Марковица. Формирование таблицы вариантов инвестиционных портфелей. Поддержка решений при оптимизации портфельных инвестиций в условиях стабильной и нестабильной экономики.
Тема 3.1. Портфельный анализ. Модель Марковица
Портфельная теория Марковица (англ. mean-variance analysis) — подход, основанный на анализе ожидаемых средних значений и вариаций случайных величин) — разработанная Гарри Марковицем методика формирования инвестиционного портфеля, направленная на оптимальный выбор активов, исходя из требуемого соотношения доходность/риск. Сформулированные им в 1950-х годах идеи составляют основу современной портфельной теории (https://ru.wikipedia.org/wiki/Портфельная_теория_Марковица).
Можно рассмотреть два различных подхода к формированию портфеля.
Первый связан с выбором активов, доходность которых стабильна, но существует не нулевая вероятность потери активов. Тогда цель портфельного анализа состоит в определении оптимального набора активов, при котором риски потерь являются минимальными. Данная стратегия портфельного анализа выражена рекомендацией: «не храните яйца (деньги) в одной корзине (в одном банке, одном активе)».
Второй подход, для которого применима теория Марковица, состоит в выборе совокупности компенсационных активов. Считается, что доходность активов является случайной величиной, но вероятности их полных потерь нулевые. Тогда цель портфельного анализа состоит в выборе совокупности активов, которая обеспечит высокую среднюю доходность (критерий 1) и минимальное отклонение уровня дохода от этого среднего (критерий 2 – риск должен быть минимальным). Снижение риска достигается использованием компенсационных активов, коэффициент корреляции доходностей которых является отрицательным. Модель Марковица позволяет выбрать оптимальный набор компенсационных активов с высокой средней доходностью.
При
записи модели используются свойства
математического ожидания и формула
математического ожидания суммы случайных
величин. Пусть для формирования
оптимального портфеля выбраны n
активов, доходность которых на период
инвестирования – случайные величины
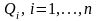с математическими ожиданиями
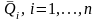и дисперсиями
.
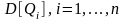Пусть
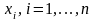– доли использования каждого актива в
формируемом портфеле, которые удовлетворяют
условиям:
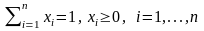. (3.1)
Тогда
доходность портфеля
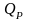на периоде инвестирования – случайная
величина, которая зависит от доходности
активов и определяется по следующей
формуле:
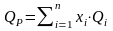. (3.2)
Найдем
математическое ожидание (среднее
значение) доходности
:
.
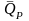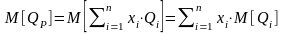Формулу для средней доходности портфеля можно записать в более наглядном виде:
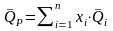. (3.3)
Из формулы (3.3) следует, что средняя доходность формируемого портфеля определяется средними доходностями активов и долями их включения в портфель.
Найдем
выражение для дисперсии доходности
портфеля
:
.
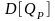Откуда получаем формулу для дисперсии портфеля в матричной записи:
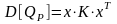. (3.4)
Здесь
вектор
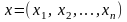– доли активов размерностью (1 × n);
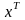– вектор столбец долей активов
размерностью (n × 1);
– ковариационная матрица активов,
которая отражает взаимозависимость
доходностей выбранных активов,
размерностью (n × n).
Модель
Марковица предписывает выбор оптимального
вектора
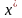долей, при котором средняя доходность
портфеля должна быть не меньше заданной
инвестором величины
(ограничение на критерий 1), а уровень
риска отклонения доходности от средней
величины был бы минимальным (минимизация
критерия 2). Математически модель
записывается с использованием выражений
(3.1), (3.3), (3.4) в следующем виде. Найти
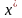из условий:
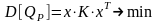; (3.5)
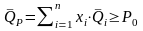; (3.6)
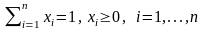. (3.7)
Задание 3.1.
Доказать, что средний уровень доходности
портфеля
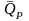изменяется в пределах:
,
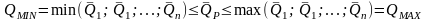т.е. от минимальной средней
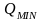до максимальной средней
доходностей выбранных активов:
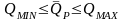. (3.8)
Учитывая
утверждение в задании 3.1, аналитику
следует рекомендовать инвестору
указанные там границы для выбора
требуемой доходности
.
Рассмотрим уровни риска для оценок реальной доходности портфеля. Обозначим границы доходности портфеля: %Низ и %Верх. Математическая статистика дает следующие доверительные интервалы для реальной доходности портфеля (см. формулу (3.2)):
%Низ
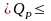%Верх, где %Низ =
;
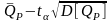%Верх =
.
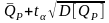(3.9)
Здесь
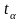– квантиль распределения доходности,
определяемый заданным уровнем
доверительной вероятности (для нормального
распределения
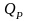и уровня значимости 5%
).
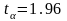Задание 3.2. Провести сравнение приведенных формул модели Марковица (3.5) – (3.7), границ изменения средней доходности портфеля (3.8) и уровней риска доходности (3.9) с формулами программы «Портфельный анализ СЭ.xls». Указать номера ячеек листа Excel, в которых вычисляются соответствующие величины.
Тема 3.2. Портфельный анализ. Формирование таблицы вариантов инвестиционных портфелей
Для
использования модели Марковица на
практике необходимо найти вероятностные
оценки ее параметров (эта задача решается
в Теме 3.3) и обосновать выбор
уровня средней доходности портфеля
.
Эту задачу решаем в данном разделе путем
формирования таблицы вариантов
инвестиционных портфелей при разных
значениях
.
В таблице 3.1 приведены 10 вариантов
портфеля, сформированного из 5 активов
(расчеты проведены в среде Excel).
Таблица 3.1. Пример вариантов портфеля,
полученных с использованием модели
Марковица при изменении
равномерно в пределах 1,8% до 5.1%.
|
№ вар |
А1 |
А2 |
А3 |
А4 |
А5 |
СД % |
ДИ% |
%Низ |
%Верх |
|
1 |
0,87 |
0,00 |
0,00 |
0,13 |
0,00 |
2,73% |
1,03% |
1,69% |
3,76% |
|
2 |
0,87 |
0,00 |
0,00 |
0,13 |
0,00 |
2,73% |
1,03% |
1,69% |
3,76% |
|
3 |
0,87 |
0,00 |
0,00 |
0,13 |
0,00 |
2,73% |
1,03% |
1,69% |
3,76% |
|
4 |
0,74 |
0,00 |
0,00 |
0,26 |
0,00 |
2,93% |
1,06% |
1,87% |
3,98% |
|
5 |
0,51 |
0,00 |
0,00 |
0,49 |
0,00 |
3,29% |
1,20% |
2,09% |
4,49% |
|
6 |
0,29 |
0,00 |
0,00 |
0,71 |
0,00 |
3,65% |
1,44% |
2,21% |
5,09% |
|
7 |
0,06 |
0,00 |
0,00 |
0,94 |
0,00 |
4,01% |
1,73% |
2,28% |
5,75% |
|
8 |
0,00 |
0,00 |
0,27 |
0,73 |
0,00 |
4,38% |
2,13% |
2,24% |
6,51% |
|
9 |
0,00 |
0,00 |
0,63 |
0,37 |
0,00 |
4,74% |
2,59% |
2,15% |
7,33% |
|
10 |
0,00 |
0,00 |
1,00 |
0,00 |
0,00 |
5,10% |
3,07% |
2,03% |
8,17% |
В
приведенной таблице первые три портфеля
совпадают по всем параметрам, так как
при выбранных исходных данных ограничение
(3.6) модели Марковица выполняется как
строгое неравенство. По остальным
портфелям наблюдается закономерность
в изменении долей активов А1 – А5,
включенных в портфель (см. данные столбцов
2 – 6 таблицы). Характерным свойством
таблицы вариантов является увеличение
риска доходности, определяемого величиной
доверительного интервала (столбец ДИ%),
с ростом средней доходности
(столбец данных СД%).
Задача аналитика состоит в обосновании рекомендации для инвестора по выбору оптимального варианта портфеля. Данная задача может быть решена с использованием экономико-математических методов принятия решений в условиях риска и неопределенности.
При использовании максиминных стратегий (принцип максимальной гарантированной доходности портфеля) оптимальным вариантом в таблице 3.1 следует считать портфель 7.
Задание 3.3. Пояснить порядок выбора варианта 7 и дать его полную характеристику.
Задание 3.4. Обосновать порядок проведения дополнительных расчетов при необходимости повышения точности расчетов оптимального портфеля.
Тема 3.3. Поддержка решений при оптимизации портфельных инвестиций в условиях стабильной и нестабильной экономики
Проведенный
выше портфельный анализ базировался
на использовании теоретических знаниях
и в модели Марковица использованы
теоретические модели процессов. Однако
в настоящее время не существует теории
для оценок параметров этой модели:
ковариационной матрицы
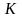в формуле (3.4) и прогнозов
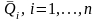средних доходностей выбранных активов
в формуле (3.3). На практике эти количественные
данные оцениваются на основе эмпирического
подхода (на основе наблюдений количественных
данных).
Следует
иметь в виду, что основной принцип
эмпирического подхода «так было, так
будет!» не всегда выполняется. Эмпирические
знания верны для стабильной экономики,
для которой комплекс закономерностей
формирования событий в прошлом без
изменения может быть перенесен на
будущее. Тогда для оценок
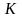и
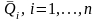можно использовать временные ряды
совместных значений доходностей в
прошлом и статистические методы их
обработки. Пример
исходных данных квартальных доходностей
5 активов представлен в таблице 3.2.
Таблица 3.2. Квартальные наблюдения процентных ставок по финансовым инструментам
|
№ квартала |
1 |
2 |
3 |
4 |
5 |
|
1 |
2,5% |
-1,4% |
2,2% |
2,3% |
-2,6% |
|
2 |
2,9% |
4,9% |
6,8% |
4,8% |
3,8% |
|
3 |
2,4% |
1,6% |
4,9% |
3,7% |
0,1% |
|
4 |
1,8% |
2,5% |
4,0% |
3,4% |
0,6% |
|
5 |
2,2% |
4,7% |
6,1% |
4,8% |
2,5% |
|
6 |
3,5% |
4,7% |
7,0% |
5,5% |
6,6% |
|
7 |
3,3% |
-0,4% |
2,9% |
3,2% |
-1,6% |
|
8 |
2,1% |
2,9% |
5,5% |
4,1% |
1,9% |
|
9 |
1,8% |
3,3% |
5,9% |
4,2% |
1,6% |
|
10 |
2,0% |
0,1% |
3,3% |
3,2% |
0,3% |
|
11 |
3,0% |
4,9% |
6,8% |
5,2% |
4,5% |
|
12 |
2,6% |
4,2% |
5,8% |
4,9% |
4,4% |
|
Сред |
2,51% |
2,67% |
5,10% |
4,11% |
1,84% |
На основе этих исходных данных в условиях
стабильной экономики можно оценить
требуемые параметры. Средние доходности
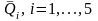активов приведены в последней строке
таблицы 3.2, а ковариационная матрица,
вычисленная с использованием встроенной
функции КАВАР() приведена в таблице 3.3.
Эмпирический подход для оценки параметров модели Марковица может быть использован в условиях нестабильной экономики, т.е. экономики, для которой в будущем сохраняются тенденции изменений экономических показателей. Тогда для поиска данных, аналогичных таблицам 3.2 и 3.3 применяют эконометрические методы анализа временных рядов.
Таблица 3.3. Оценки ковариационной матрицы
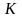формулы (3.4) по данным таблицы 3.2.
|
i\j |
1 |
2 |
3 |
4 |
5 |
|
1 |
2,925E-05 |
1,667E-05 |
1,948E-05 |
1,877E-05 |
5,062E-05 |
|
2 |
1,667E-05 |
0,000456 |
0,000323 |
0,000188 |
0,000498 |
|
3 |
1,948E-05 |
0,000323 |
0,000245 |
0,000139 |
0,000368 |
|
4 |
1,877E-05 |
0,000188 |
0,000139 |
0,000086 |
0,000229 |
|
5 |
5,062E-05 |
0,000498 |
0,000368 |
0,000229 |
0,000659 |
Состояние экономики, для которой принципы эмпирического моделирования процессов неприменимы, называется кризисной. Профессиональные знания и опыт аналитика направлены на надежную оценку состояния экономики при решении конкретной аналитической задачи.
Методические подходы портфельного анализа в среде Excel с использованием инструмента «Поиск решения» в условиях стабильной и нестабильной экономик приведены в описании соответствующих лабораторных работ.