ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 07.07.2019
Просмотров: 1384
Скачиваний: 13
16
окружают нейтронный остов. В лѐгких ядрах количество нейтронов в
завершенном остове совпадает с количеством протонов в завершенной
оболочке из-за особенностей строения. Если нейтронов в ядре больше
количества протонов и количества нейтронов в завершенном остове, то
ядро перегружено нейтронами. Если количество протонов в ядре меньше
количества нейтронов и количества нейтронов в завершенном остове, то в
ядре существует дефицит протонов. Если количество протонов в ядре
больше количества нейтронов и количества нейтронов в завершенном
остове, то ядро перегружено протонами. Количество нейтронов в ядре
слабо зависит от количества протонов. Например, к шести нейтронам
нейтронного кольца снаружи может прилипнуть максимум шесть
протонов. А могут и не прилипнуть…
Рисунок 5-3. Электронное облако атома с завершенной p-орбиталью и его ядро
Утолщаясь и укорачиваясь, слипаются друг с другом и связанные с
протонами электронные лепестки в электронной оболочке атома,
формируя полностью заполненную электронную p-орбиталь. Лепестки
незавершенных p-орбиталей могут взаимодействовать с электронными
оболочками других атомов, формируя молекулярные связи.
Слипшиеся между собой лепестки полностью заполненной p-
орбитали таких связей сформировать не способны – они инертны. При
внешних воздействиях возможен переход протона из одной протонной
оболочки в другую, соседнюю незавершенную протонную оболочку.
Рисунок 5-4. Примеры переходов протона из одной ядерной оболочки в другую
Наиболее сильное электростатическое взаимодействие происходит
между полюсами протонов. По этой причине соседние протонные
оболочки одного типа должны отталкиваться друг от друга, разрывая ядро.
17
Рисунок 5-5. Расталкивание ядерных оболочек одного типа
В соседстве друг от друга могут находиться только протонные ядерные
оболочки разного типа.
Рисунок 5-6. Примеры принципа чередования оболочек
В данной модели вращающая полностью заполненная ядерная s-оболочка
формирует вращающуюся электронную s-оболочку атома. Такой комплекс
двух оболочек способен полностью экранировать отталкивание друг от
друга соседних ядерных p-оболочек. В свою очередь, p-оболочка
экранирует отталкивание друг от друга соседних ядерных s-оболочек.
Например, в ядре неона чередуются полностью заполненные две s-
оболочки и одна p-оболочка. А в ядре аргона чередуются три s-оболочки и
две p-оболочки.
Рисунок 5-7. Изображение ядер Ne20, Si28, S32 и Ar36
В нашей модели теоретически возможна ещѐ одна ядерная оболочка,
которой, по современным научным представлениям, не соответствует
какая-либо электронная подоболочка в атоме. Поэтому обозначим еѐ как
усечѐнная модификация ядерной p-оболочки.
Рисунок 5-8. Возможное существование ядерной оболочки с 4 протонами
18
6.
Вычисление спина ядра
Механистическая модель строения ядер атомов позволяет вернуть спину
первоначальный механический смысл. Спин ядра представляет собой
сумму спинов составляющих ядро нуклонов с учетом знака спина. Спин
нуклона – механический момент вращения. Его величина зависит от
скорости вращения нуклона вокруг собственной оси и от расстояния до
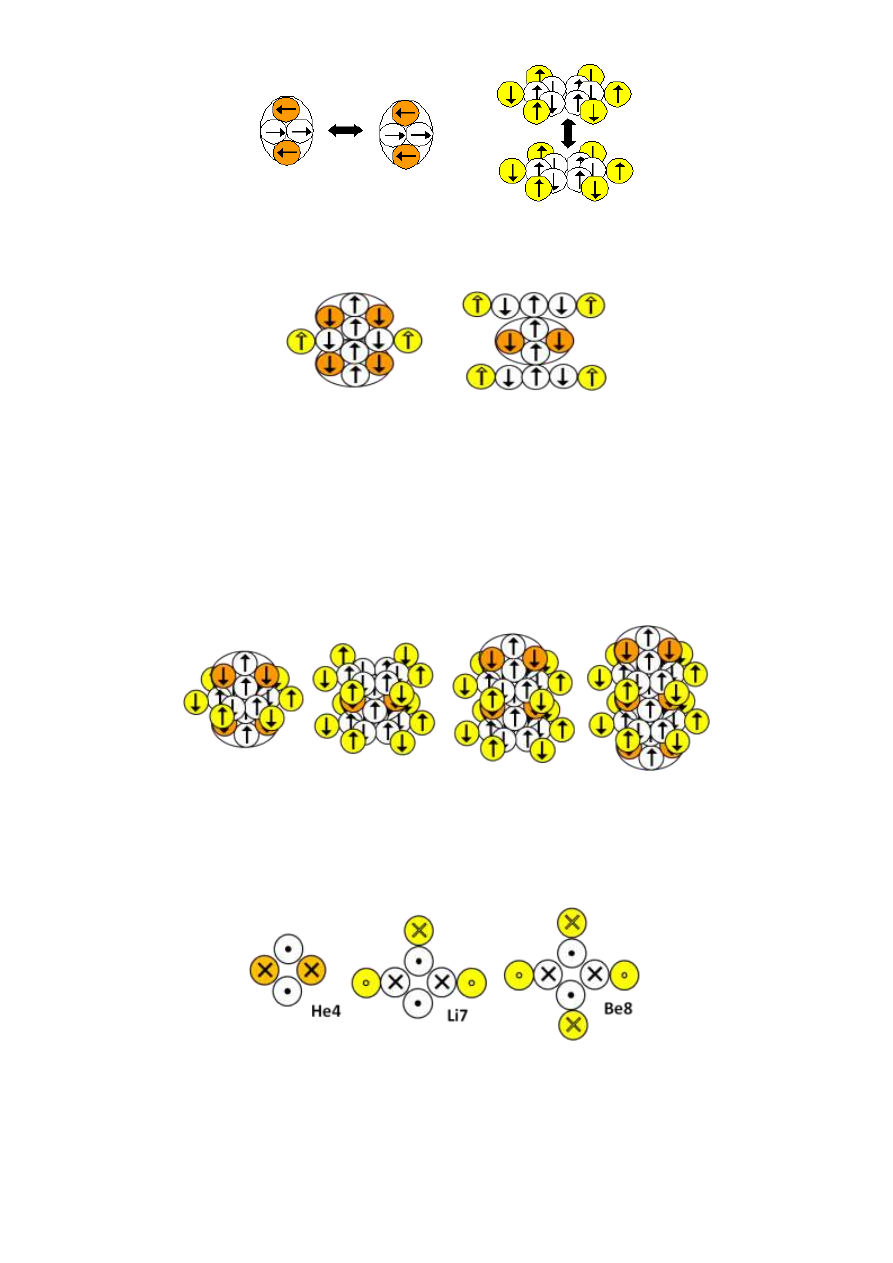
оси измерения, чаще всего являющейся и осью симметрии ядра. Так как
собственное вращение нуклона постоянно, то изменяться может только
расстояние до оси измерения. При плотной упаковке расстояние до оси
измерения принимает только дискретные величины, кратные радиусу
нуклона. Соответственно, спин нуклона тоже может иметь только
дискретные значения, так как, согласно данной модели, все вектора
моментов вращения параллельны оси измерения. Нуклоны, находящиеся в
центре ядра на оси симметрии орбитального момента вращения не имеют,
поэтому их суммарный момент вращения равен внутреннему спину (1/2).
У статических нуклонов, находящихся на некотором расстоянии от оси
симметрии, суммарный момент вращения равен сумме внутреннего спина
и статического орбитального момента вращения и вычисляется по
формуле (1/2)+k*(1/2), где k - расстояние в радиусах от оси измерения до
центра нуклона. Единственным исключением является расчѐт полного
спина для динамических протонов полностью заполненной ядерной s-
оболочки. Статический орбитальный момент у таких протонов полностью
компенсируется динамическим орбитальным моментом, создаваемым при
вращении протона вокруг нейтронной оси. Поэтому их полный момент
вращения равен внутреннему спину. На рисунке ниже показан расчѐт
полного спина для ядер гелия. Овал вокруг нуклонного комплекса
подчѐркивает, что протоны вращаются вокруг нейтронной оси.
Рисунок 6-1. Расчѐт полного спина для ядер гелия
Для точного подсчета спина ядра достаточно знать точное расстояние от
каждого нуклона до оси симметрии и ориентацию спина нуклона. Это
возможно при наличии графического изображения пространственной
конфигурации ядра. Но с графическим изображением не всегда удобно
работать. Иногда необходимо использовать математическое либо
символьное описание. Существующее символьное описание электронных
оболочек для данного случая явно не подходит - нет четкой системы
обозначений. Обозначение должно естественным образом указывать на
относительную координату нуклона в ядре. При плотной упаковке
нуклоны располагаются слоями. Для удобства символьного описания,
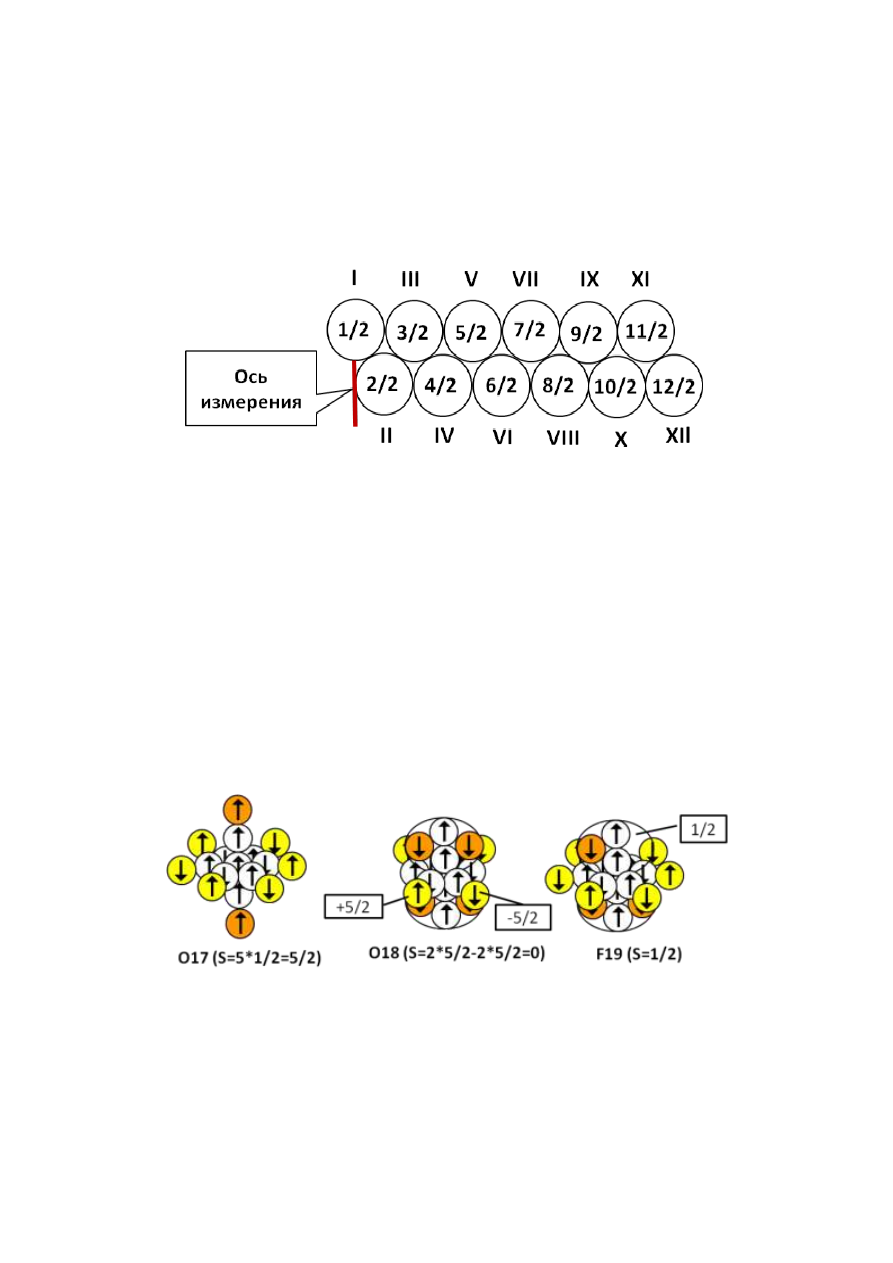
19
можно, например, присвоить каждому слою уникальное обозначение,
используя римские цифры последовательно. Цифру „I‟ используем для
обозначения слоя нуклонов, находящихся на оси симметрии.
Последующие цифры будем последовательно использовать для
обозначения слоѐв нуклонов, находящихся на последующих дискретных
расстояниях (орбитах) от оси симметрии (измерения). Полный спин ядра
вычисляется как арифметическая сумма спиновых (s=1/2) и орбитальных
(l) моментов составляющих ядро нуклонов с учѐтом знаков.
Рисунок 6-2. Полный спин нуклона в зависимости от расстояния до оси
Нуклоны, находящиеся на орбите „III‟, могут вращаться вокруг оси
симметрии (1 или 2 нуклона с одинаковым направлением спина). В этом
случае суммарный спин нуклона уменьшается до значения “1/2”. Во всех
остальных случаях нуклоны не имеют орбитального вращения и имеют
суммарный спин согласно рисунку выше. Протонам, находящимся на слое
„I‟ или „III‟, соответствуют s-электроны электронной оболочки атома. По
официальной терминологии, эти протоны находятся на ядерной s-
оболочке. Протонам, находящимся на слое „V‟, в электронной оболочке
атома соответствуют p-электроны. По официальной терминологии, эти
протоны находятся на ядерной p-оболочке. Протонам, находящимся на
слое
„VII‟,
соответствует
официальная
d-оболочка.
Протонам,
находящимся на слое „IX‟, соответствует официальная f-оболочка.
Рисунок 6-3. Подсчѐт полного спина через спин незаполненных оболочек
У любой полностью заполненной ядерной оболочки спин всегда равен
нулю. Поэтому можно подсчитывать только спин незаполненных
оболочек. А если в оболочке не хватает всего одного нуклона, то полный
спин ядра равен спину недостающего нуклона.
20
7.
Вычисление чётности ядра
Приведѐнные в справочниках данные по чѐтностям ядер являются
значениями, вычисленными в квантовой механике как реакция уравнения
Шрѐдингера на инверсию координат в теоретически созданной волновой
функции, математически описывающей ядро атома. То есть, в отличие от
спина, чѐтность ядра экспериментально не измеряется. По этой причине
не правомерно вычисленную чѐтность ядра в нашей модели сравнивать со
справочными данными. Но сравнивать придѐтся, потому что больше не с
чем сравнивать. В квантовой механике определение чѐтности ядра атома
осуществляется математическим способом: чѐтность ядра является
произведением чѐтностей всех его нуклонов, чѐтность нуклона равна (-1)
L
,
где L - его орбитальный целочисленный момент в математической модели
ядра. По исходному физическому определению чѐтность ядра атома
должна
определяться
другим образом:
чѐтность
микрообъекта
положительна, если при инверсии координат, называемой P-отражением,
состояние микрообъекта не изменяется. В нашей теории модели ядер не
математические, а физические, поэтому операцию инверсии координат
возможно осуществлять на физическом уровне наглядно в трѐхмерном
пространстве. Согласно физическому определению P-отражения, должна
осуществляться инверсия координат каждого нуклона трѐхмерной модели
(x на –x, y на –y, z на –z), при этом направление спина нуклона не
меняется. Такую трѐхмерную инверсию осуществить легко. Гораздо
трудней интерпретировать результаты инверсии. Например, при инверсии
координат полностью заполненной ядерной p-оболочки происходит
поворот трѐхмерной конфигурации вокруг оси симметрии (оси z).
Рисунок 7-1. Инверсия координат ядра C12
Какая чѐтность такого ядра, если после инверсии координат его состояние
в пространстве изменилось (он повернулся вокруг своей оси симметрии)?
По формуле квантовой механики нужно перемножить чѐтности всех
нуклонов. Мы имеем два слоя: слой „III‟ с шестью нейтронами и слой „V‟ с
шестью протонами. Для слоя „III‟ L=1, поэтому чѐтность нейтронов в этом
слое (-1)
L
= -1. Для слоя „V‟ L=2, поэтому чѐтность протонов (-1)
L
= +1.
Суммарная чѐтность ядра положительна (-1)
6
* (+1)
6
=+1.
Спин ядра равен нулю (3*3/2 - 3*3/2 + 3*5/2 - 3*5/2)
Для быстрого подсчѐта чѐтности ядра по формуле достаточно знать, что
чѐтность положительная у полностью заполненной ядерной оболочки, у
нуклонных слоѐв с нечѐтным L с чѐтным количеством нуклонов, у