Файл: Информация в материальном мире (подробно).pdf

В 1865 году немецкий физик Рудольф Клаузиус ввел в статистическую физику понятие энтропии или меры равновесия системы. В 1921 году основоположник большей части математической статистики, англичанин Рональд Фишер впервые ввел термин «информации» в математику, но полученные им формулы весьма своеобразны [8].

В 1948 году Клод Шеннон в своих работах по теории связи пишет формулы для вычисления количества энергии и энтропии [5]. Термин «энтропия» используется Шенноном по совету Патриарха компьютерной эры фон Неймана, который отметил, что Формулы Шеннона для расчета теории связи совпадали с соответствующими формулами статистической физики, а также тот факт, что «никто точно не знает», что такое энтропия.

Энтропия – это мера неопределенности системы, в частности непредсказуемости появления любого первичного символа алфавита. В последнем случае, при отсутствии потерь информации, энтропия численно равна количеству информации на символ передаваемого сообщения [2].

Например, в последовательности букв, составляющих предложение на русском языке, разные буквы появляются с разной частотой, поэтому неопределенность появления для одних букв меньше, чем для других. Если учесть, что некоторые сочетания букв, в данном случае, говорят об энтропии очень редко, то неопределенность уменьшается еще больше [8].

Хартли ввел аддитивную двоичную логарифмическую меру, позволяющую вычислять количество информации в двоичных единицах – битах [15]:

(1)

При n = 1, q = 2 . Это и есть единица информации Хартли (1). Следовательно, 1 бит информации соответствует одному элементарному событию, которое может произойти или не произойти. Такая мера количества информации удобна тем, что дает возможность оперировать мерой как числом. Количество информации эквивалентно количеству двоичных символов 0 или 1 [6].

Существует взаимосвязь меры Шеннона с мерой Хартл. Если в источнике может быть реализовано h равновероятных состояний, то вероятность каждого из них , с учетом этого меру неопределенности источника Хартли можно трактовать, как количество информации, приходящей на одно дискретное сообщение (поскольку все сообщения источника равновероятные количества информации в каждом из них равны) [8]. В то же время, энтропия по Шеннону – это среднее количество информации, содержащееся в одном из не равновероятных состояний. Она позволяет учесть статистические свойства источника информации. Наряду с рассмотренными мерами Хартли и Шеннона существуют и другие подходы к определению количества информации. Наиболее интересной, наиболее новой явилась информационная концепция Колмогорова [8]. Ее основным тезисом является то, что на основании определения энтропии количество информации связывается с вероятностью наступления P_i. Это выглядит достаточно разумно, т.к. понятие вероятности имеет смысл лишь в связи с массовыми явлениями количества единиц информации в единичном акте и представляющих интерес в связи с данным исходом, оказывается выраженным через вероятности массовых явлений [15].

Основные понятия теории информации могут быть обоснованы без обращения к теории вероятностей, причем так, что понятия энтропии и количества информации строго приемлемы для отдельных объектов. Однако мера Шеннона интересна не сама по себе, а как основа встроенной теории, позволяющей изменять и расширять существующие предположения о возможностях в области коммуникационных технологий [7].

Выводы по первой главе: определить понятие информации стало для человека жизненно важной необходимостью, так как просто из сведений, которые нас окружают информация стала превращаться в товар, продукт, который имеет свою стоимость. Также очень важно использовать различные подходы к определению количества информации. Измерение объема информации на основе вероятностных событий или с точки зрения информационной концепции будет давать человеку представление о том какое количество информации накопилось или будет накоплено и какое объем для хранение этого объема информации будет необходим.

Глава 2. Характеристика процессов сбора, передачи, обработки и накопления информации

2.1. Сбор информации

Сбор информации является одним из важнейших этапов информационного процесса и в широком смысле означает процесс комплектования системы информационного обеспечения массивами первичных и вторичных документированных источников информации. Применительно к информационным системам, созданным с использованием ЭВТ, используется понятие сбора данных [10].

Сбор данных (data collection) - это процесс идентификации и получения данных из различных источников, группировки полученных данных и представления их в форме, необходимой для ввода в компьютер [8].

Сбор информации связывает систему информационного обеспечения с внешней средой. Эффективность процесса сбора информации (информационного массива) оценивается по показателям полноты, точности, оперативности, актуальности, стоимости, трудоемкости [10].

Полнота - это количественная мера содержания в массиве всех соответствующих документов (информации), существующих в данный момент времени с точки зрения всех пользователей системы [10].

Пертинентность - соответствие содержания документа (информации) информационным потребностям пользователей [15].

Точность - это количественная мера содержания массивов данных (системы) только соответствующих документов (информации). Этот показатель характеризует внутреннее состояние процесса сбора информации, его способность удовлетворять информационные запросы независимо от времени поиска информации [8].

Эффективность - способность процесса сбора выполнить задачу в кратчайшие сроки [8].

Стоимость - способность процесса сбора минимизировать затраты ресурсов на единицу информационного массива [15].

Трудоемкость - способность процесса сбора минимизировать трудозатраты на единицу информационного массива [8].

В рамках процесса сбора осуществляется структурирование информации, определение информационных потребностей объекта (пользователя) и выбор источника информации. Задачей структурирования информации [7] является системная классификация информации с точки зрения удобства ее использования человеком в процессе решения практических задач и удобства обработки и хранения с использованием современных средств и методов.

Выбор источника информации должен основываться из следующих требований: полнота информации, достоверность информации, актуальность информации, релевантность информация, информативность, толерантность информации, функциональная направленность, законность предоставляемой информации, регулярность поступления информации, минимизация затрат ресурсов на ведение информационного инвентаря [9].

Задача оптимального выбора источников информации заключается в выборе из всего имеющегося потенциала наборы таких агрегатов, которые при минимальных затратах затрат и труда будут обеспечивать удовлетворительное регулярных получение необходимой информации, соответствующей перечисленным с вышеуказанными требованиями [14].

Решение таких задач осуществляется известными методами многокритериальная оптимизация.

Многокритериальная оптимизация – способ решения задач нахождения наилучшего (оптимального) результата, удовлетворяют нескольким и не сводимым друг к другу критериям [8].

2.2. Подготовка и передача информации

Этап подготовки информации, обрабатываемой информационными системами информации, связан с известным процессом формирования структуры информационного потока, представленного в цифровом виде [10]. Для этого мы используем кодирование информации. Способы представления кодов основаны на применении теорий связей, алгебраических преобразований и геометрических конструкций. Коды, как известно, могут быть представлены формулами, геометрическими фигурами, таблицами, графами, полиномами, матрицами и т. д. примером использования теории связей при формировании кодов является то, что количество комбинаций определяется выбранным методом кодообразования, количеством качественных признаков и общим числом элементов кода [3]. Код можно задать в виде формулы размещения, где кодовые слова представляют собой комбинации, отличающиеся как по самим элементам, так и по порядку их расположения (2):

где m- число качественных признаков (алфавита) кода; n – количество элементов кодового слова. С учетом этого выражения максимальное количество размещений будет при n = m – 1. Можно задать код, в котором кодовые слова представляют соединения, отличающиеся только порядком входящих в них элементов. Для этого используется, формула перестановок [8]:

где m – число качественных признаков (алфавит) кода. Если код представляет собой соединения, отличающиеся только самими элементами, то он задается в виде формулы сочетаний:

Максимальное число сочетаний получается при n = m/2 (для четных m) и n = (m+1)/2 (для нечетных m).

Пример. Для алфавита a, b, c, m = 2, а 3 кодовые слова имеют вид ab, ac, bc. Представление кода в виде многочлена для любой системы счисления с основанием Р соответствует выражению [15]:

Передача информации в широком смысле рассматривается как рассмотрены процесс и способы формирования и циркуляции информационного потока, который в общем виде представляет собой движение структурированной информации в некоторой информационной среде [10]. Информационные потоки на объекте делятся на входные, внутренние и выходные. В телекоммуникационном канале их можно разделить на односторонние и двухсторонние. Циркуляцией информационных потоков называется факт их регулярного перемещения между различными объектами или между ними различными элементами одного и того же объекта. Основными процессами, обеспечивающими циркуляцию информационных потоков, можно представить в виде схемы (Рис. 2) [15].

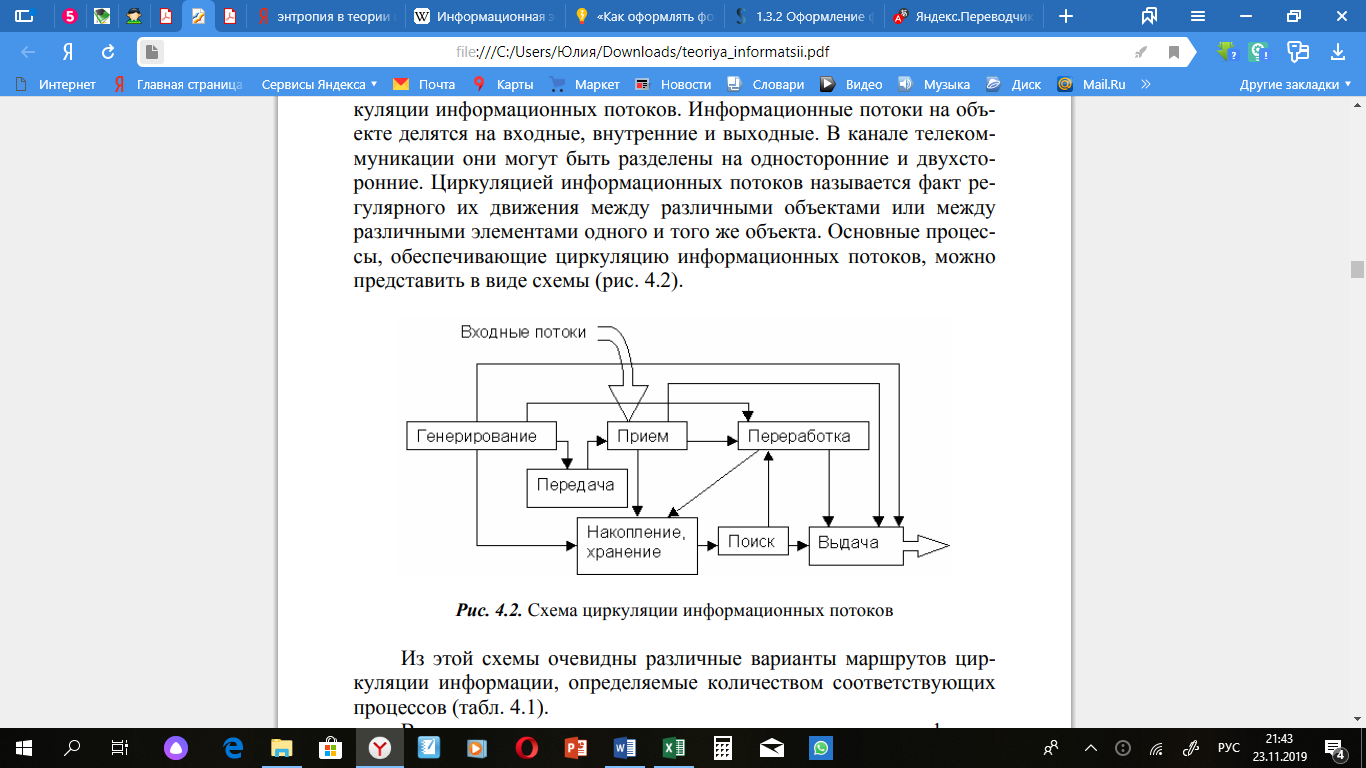
Рисунок 2. Схема циркуляции информационных потоков.

Схемы очевидно отражает различные варианты маршрутов циркуляции информации, определяемые количеством релевантных процессы (Рис. 2).

Важное место здесь занимает процесс передачи информации, заключающийся в ее транспортировке с места генерации (от источника) к местам хранения, переработки или использования (потребителю) [10].

В существующих информационных системах различных классов в зависимости от типа используемого носителя и средства обработки можно выделить: устную передачу в прямом общении; передачу бумажных носителей с использованием курьерско-почтовая связь; передача машиночитаемых носителей информации (магнитные карты, перфокарты, перфоленты, магнитные диски и ленты) посредством курьерской почтовой связи; передача в виде различных электрических сигналов по телекоммуникационным каналам связи, в том числе связь по автоматизированным каналам связи [8].

Несмотря на широкое использование технических средств связи, продолжает использоваться курьерская почта коммуникация, в которой передача информации может быть представлена в виде общей схемы (Рис. 3) [8].

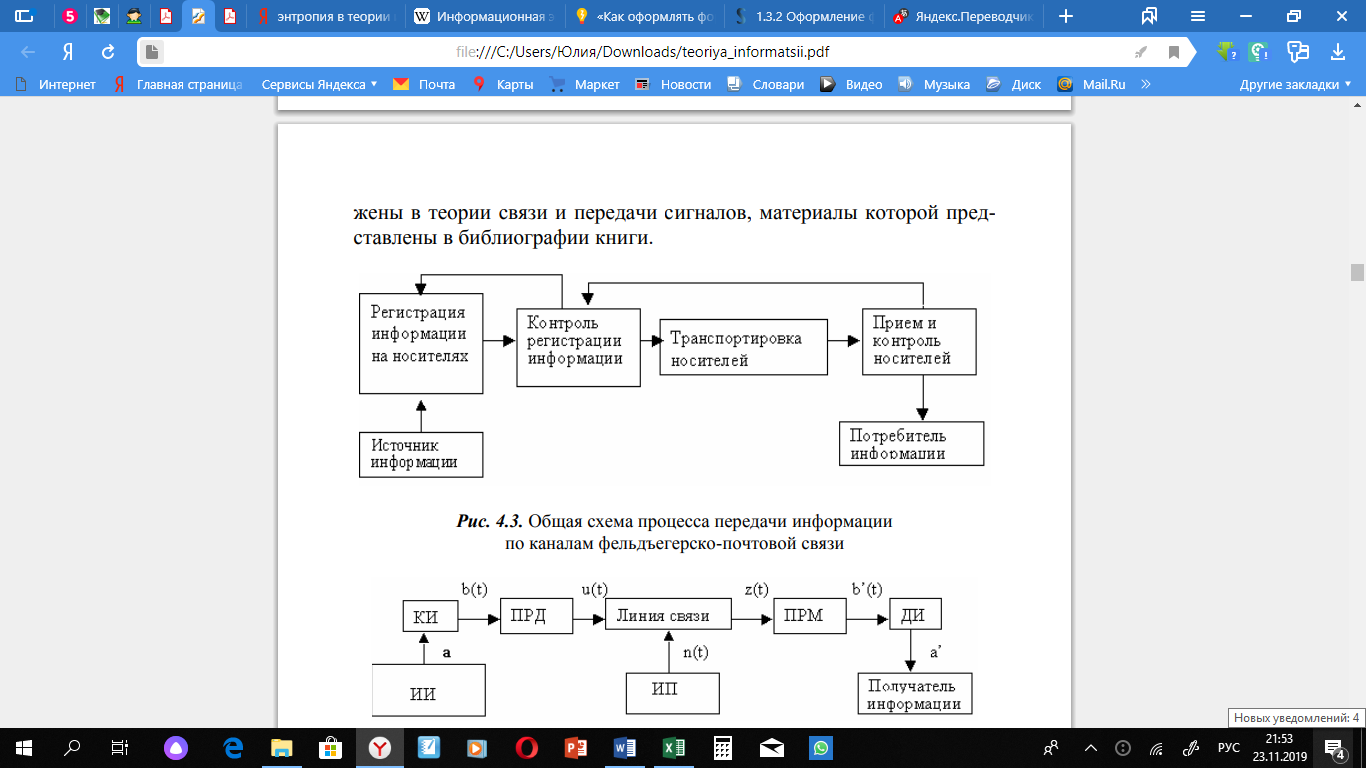
Рисунок 3. Общая схема процесса передачи информации по каналам фельдфебельской почтовой службы.

В современных информационно-телекоммуникационных системах передача информации по каналам связи обычно представлена схемой (Рис. 4).

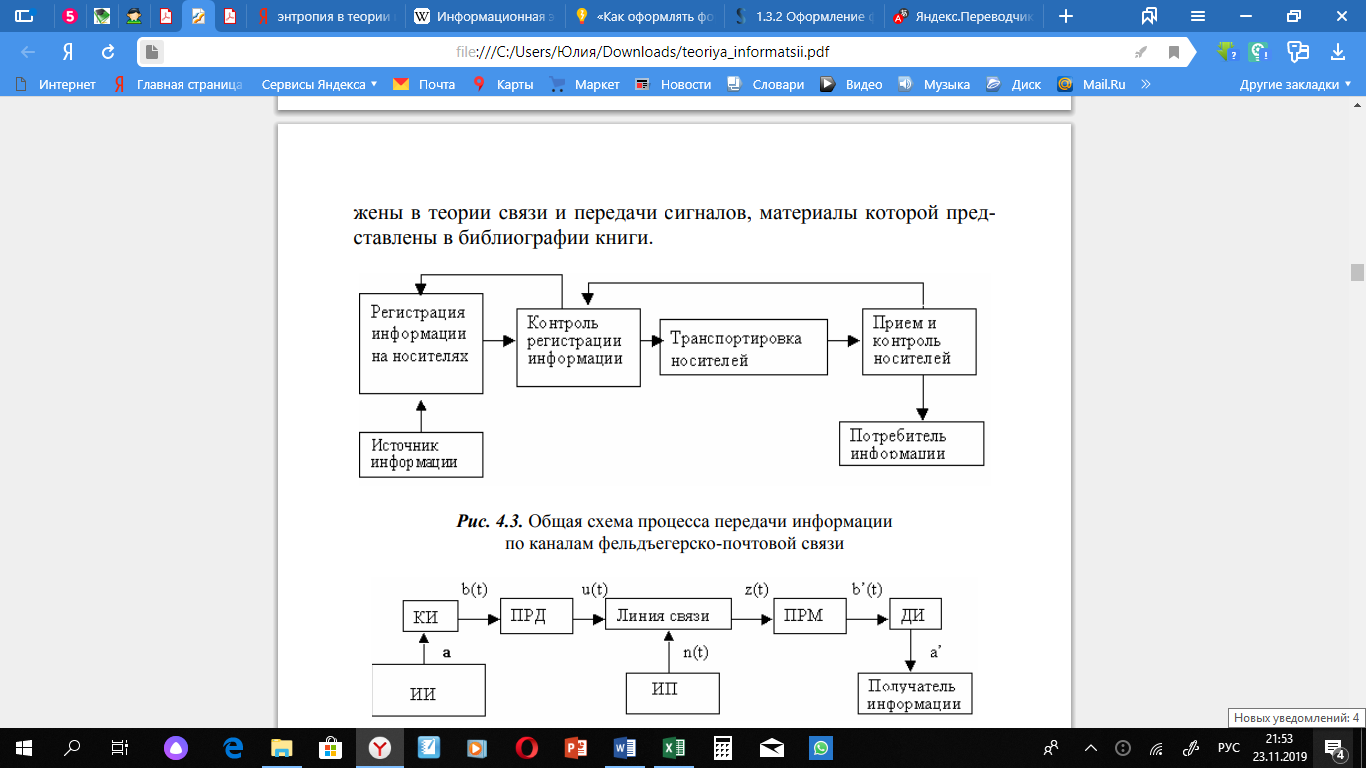
Рисунок 4. Общая схема передачи информации по каналам телекоммуникаций (связи)

Источником информации (ИИ) и ее получателем может быть, как человек, так и различные технические устройства (средства связи, ЭВТ и др.). С помощью кодера исходного устройства (КИ) информация, имеющие любую физическую природу (изображение, звук и т.), преобразуется в первичный электрический сигнал b(t). Для получения непрерывной информации, такой как голосовое сообщение, эта операция сводится к преобразованию звукового давления в пропорциональное изменение электрического тока микрофона, который в каждом момент отсчета (время) может быть представлен конечным числом сигналов, соответствующих отдельным символам исходного алфавита [15].

В телеграфии, последовательность элементов сообщения (букв алфавита) большое количество заменяемых (закодированных) символов (буквы) другого меньшего алфавита. Дальше с помощью технического устройства последовательность кодовых символов преобразуется в последовательность электрических сигналов [].

Процесс преобразования букв сообщений в сигналы преследует несколько целей. Первая цель заключается в преобразовании информации в систему символов, обеспечивающих простоту и надежность аппаратной реализации информационных устройств, а также их эффективность [5]:

• простота технических средств распознавания элементарных символы сообщения;
• сокращение избыточности символов, необходимых с буквой сообщения;
• минимальное время передачи или минимальное количество запоминающих устройств, хранящих информацию;
• простота выполнения арифметических и логических действий с сохраненной информацией.

Кодирование при отсутствии помех в канале связи дает выигрыш во времени передачи или объеме памяти запоминающего устройство, т. е. повышает эффективность работы системы. Это называется эффективным или оптимальным кодированием [5].