Файл: Митяков Информатика Часть 1.pdf

46 

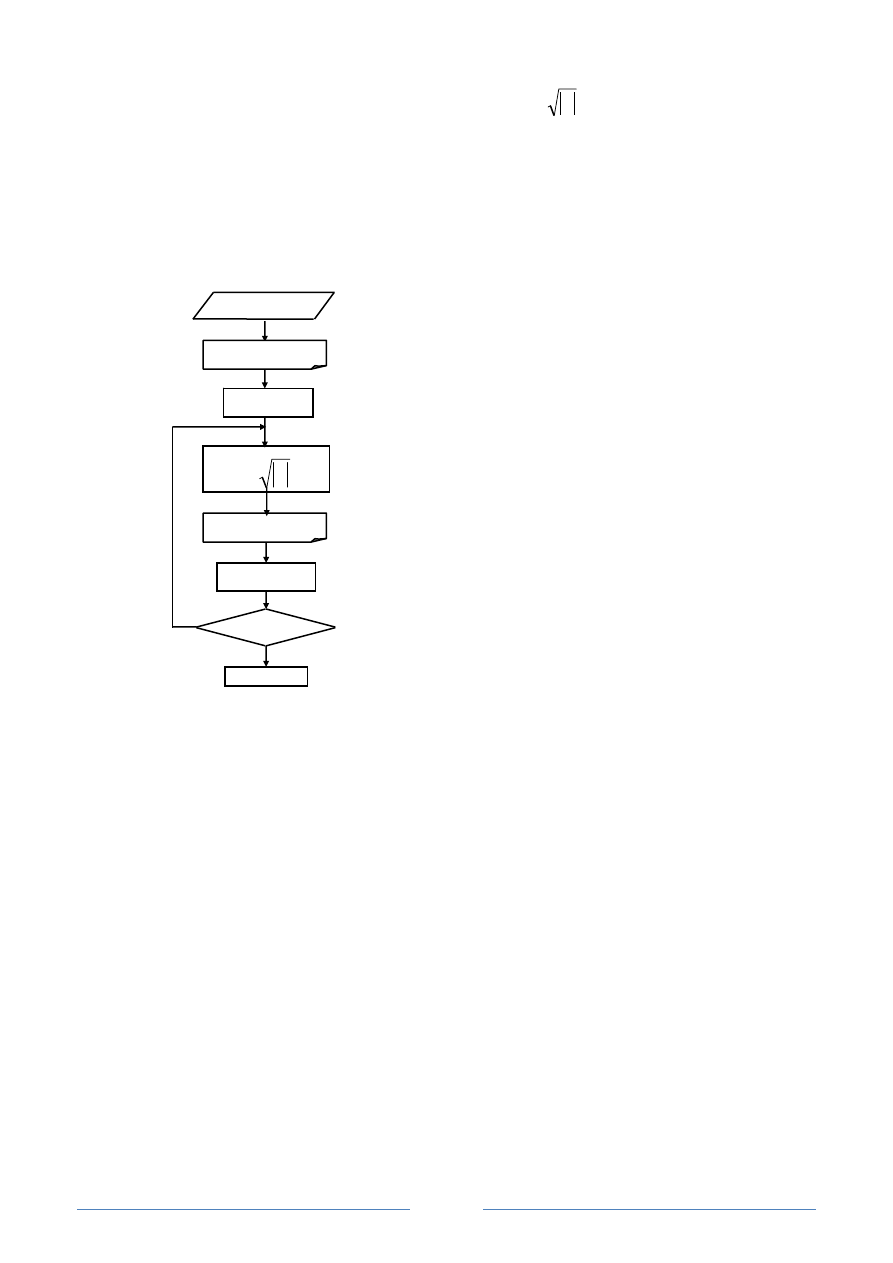
Пример 1. Вычислить  таблицу  значений  y=

x

  при  x,  изменяющемся  в 

интервале [xn;xk] с шагом hx. Параметры цикла xn, xk, hx задаются произвольно. 

Телом цикла в данном примере является линейный алгоритм, состоящий 

из двух блоков: блока вычислений и блока печати.  

Блок-схема 

Программа на Фортране 

WRITE(*,*) ’Введите xn,xk,hx’    
READ(*,*) xn,xk,hx 
WRITE(*,*) ’   x      y’ 
x=xn 

10    y=SQRT(ABS(x)) 

WRITE(*,*) x,y 
x=x+hx  
IF (x.LE.xk) GOTO 10  
END 

Одномерный циклический алгоритм реализуется, если имеется лишь одна 

переменная  цикла.  Рассмотрим  случай,  когда  телом  цикла  является  разветв-

ляющийся алгоритм. 

Пример 2. Вычислить таблицу значений функции 

⎩

⎨

⎧

>

≤

+

+

=

3

,

1

x

если 

,

ax

;

3

,

1

x

если

,

c

bx

ax

y

2

при различных значениях переменной x, изменяющейся в интервале от xn 

= 0,1 до xk = 0,4. по закону арифметической прогрессии с шагом hx = 0,1. Здесь 

a, b, c – заданные константы (a = 0,5; b = 1; c = 2). 

xn, xk, hx 

x

y

=

x=xn 

x=x+hx 

x

≤ xk 

конец 

да 

нет 

’   x     y’

x, y

47 

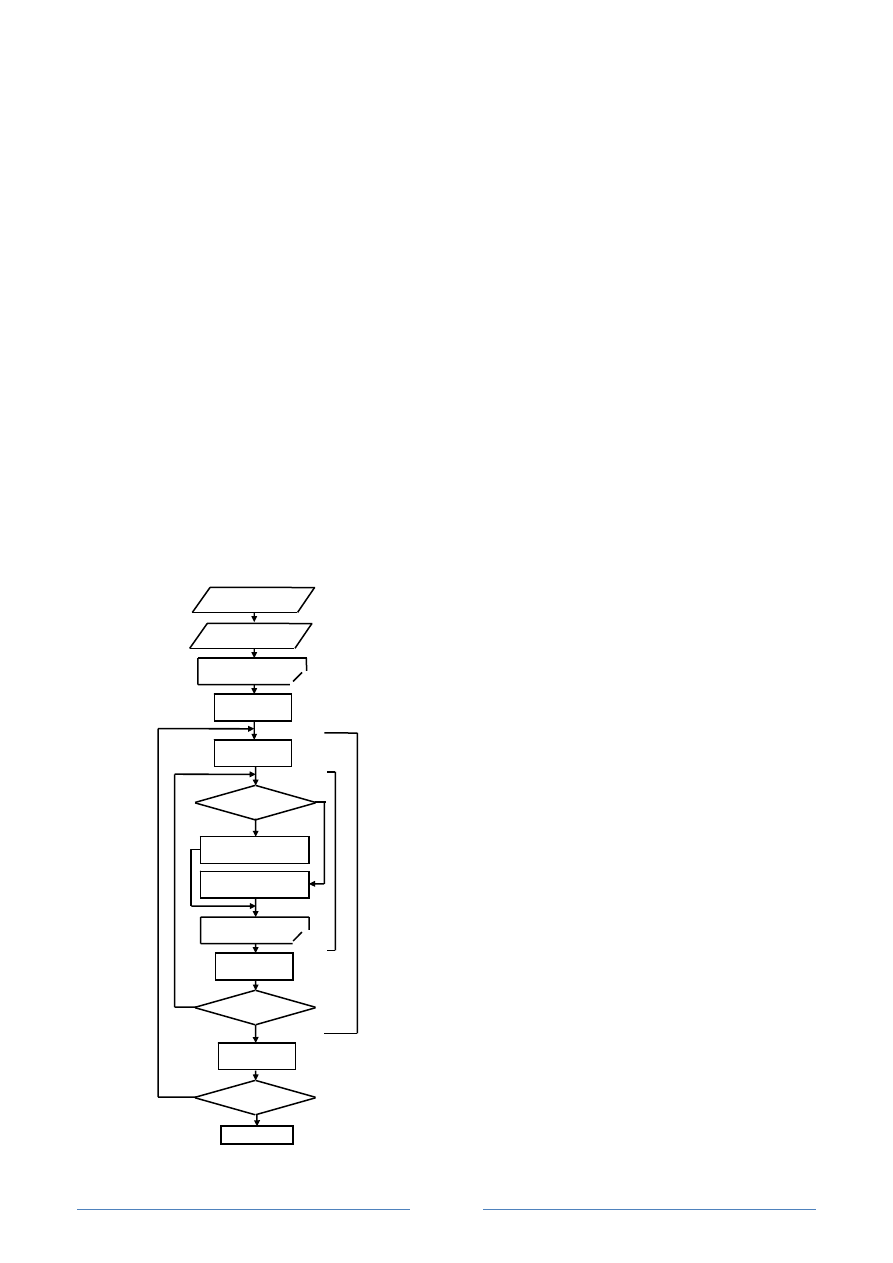
Блок-схема 

Программа на Фортране 

WRITE(*,*) ’Введите a,b,c’    
READ(*,*) a,b,c 
WRITE(*,*) ’Введите xn,xk,hx’    
READ(*,*) xn,xk,hx 
WRITE(*,*) ’   x      y’ 
x=xn 

4  IF (x.LE.1.3) GOTO 5 

y=ax 
GOTO 6 

5  y=a*x**2+b*x+c 
6  WRITE(*,*) x,y 

x=x+hx  
IF (x.LE.xk) GOTO 4  
END 

Часто бывает полезным перед тем, как запустить программу на счет, про-

крутить алгоритм вручную. Приведем ручную прокрутку данного алгоритма. 

1.

Ввод исходных данных и параметров цикла. 

2.

Печать заголовка таблицы. 

3.

Присвоение начального значения переменной цикла x = 0,1. 

4.

x

≤ 0,3 – да; y = ax = 0,5*0,1 = 0,05; печать 0,1 0,05; x = 0,2; x≤ 0,4 – да. 

5.

x

≤ 0,3 – да; y = ax = 0,5*0,2 = 0,1; печать 0,2 0,1; x = 0,3; x≤ 0,4 – да. 

6.

x

≤ 0,3 – да; y = ax = 0,5*0,3 = 0,15; печать 0,3 0,15; x = 0,4; x≤ 0,4 – да. 

7.

x

≤ 0,3 – нет; y = ax2+bx+c = 0,5*0,4*0,4+1*0,4+2 = 2,48; печать 0,4 2,48; x   

= 0,5; x

≤ 0,4 – нет. 

8.

Конец. 
Циклический алгоритм, содержащий в теле цикла циклы по другим пере-

менным, называется многомерным циклом. Правило построения многомерных 

циклов: 

a,b,c 

x=xn

x

≤ xk 

конец 

да 

нет 

заголовок 

xn, xk, hx 

x, y 

y=ax

2

+bx+c 

x

≤ 0.3 

да 

нет 

x=x+hx 

y=ax 

48 

1. Вначале записываются блоки начального присвоения, начиная с самого   

внешнего и кончая самым внутренним циклом. 

2. Далее следует тело самого внутреннего цикла. 

3.  В  заключение  записываются  парами  блоки  №3  и  №4 (приращения  и 

проверки условия продолжения цикла), начиная с самого внутреннего и кончая 

самым внешним циклом. 

Рассмотрим  пример  двумерного  циклического  алгоритма,  в  котором  те-

лом внутреннего цикла является разветвляющийся алгоритм. 

Пример 3. Вычислить таблицу значений функции 

⎩

⎨

⎧

>

≤

=

3

,

1

x

если 

,

ax

;

3

,

1

x

если 

,

ax

y

2

так,  что  для  каждого  значения  а,  изменяющегося  в  интервале  [an;ak]  с  шагом 

ha, переменная x принимает все значения в интервале [xn;xk] с шагом hx. 

Блок-схема 

Программа на Фортране 

WRITE(*,*)’Введите an,ak,ha’ 
READ(*,*) an,ak,ha 
WRITE(*,*)’Введите xn,xk,hx’ 
READ(*,*) xn,xk,hx 
WRITE(*,*)’ a    x    y’ 
a=an 

20 x=xn 
15  IF (x.LE.1.3) THEN 

y=a*x**2 
ELSE 
y=a*x 
END IF 
WRITE(*,*) a,x,y 
x=x+hx 
IF (x.LE.xk) GOTO 15  
a=a+ha 
IF (a.LE.ak) GOTO 20 
END 

y=ax

т 

е 

л 

о 

ц 

и 

к 

л 

а 

п 

о 

x

т 

е 

л

о 

ц

и

к

л

а 

п

о 

a

an,ak,ha 

xn,xk,hx

a=an

’a  x   y’

x=xn

x

≤ 1,3

y=ax2

x=x+hx 

a=a+ha 

x

≤ xk

a

≤ ak

конец

да 

да 

нет 

нет 

нет 

да 

a,x,y

49 

Пример 4. Поиск  экстремального  значения  функции  методом  простого 

перебора значений аргументов. 

Найти значения x, y, z с наименьшим z = f(x,y). Каждый из аргументов x, y 

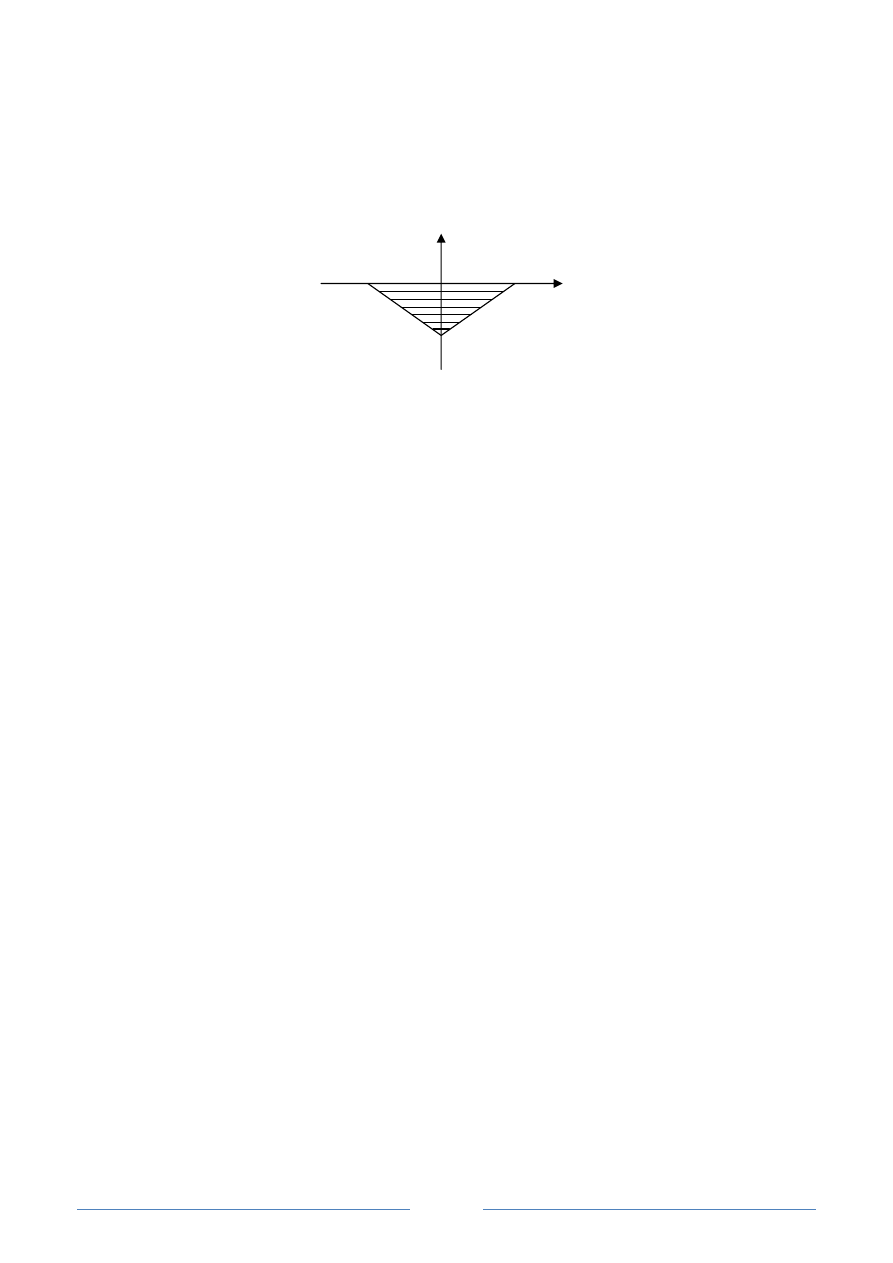
изменяется с заданным шагом в заданной области (см. рис. 10.).  

Рис. 10. Иллюстрация к примеру 4 

 
В данном случае область ограничена сверху осью абсцисс (y=0), а снизу – 

двумя прямыми y=x-2 и y=-x-2. Пусть z=2x+3y-2xy; hx =0,2; hy = 0,1.  Условие  

ограничения снизу имеет вид: y 

≥

 x-2 и y 

≥

 -x-2. Минимальное значение функ-

ции  z  и  соответствующие  значения  аргументов  будут  расположены  в  ячейках 

zm, xm, ym, причем в начале программы идет присвоение zm = f(xn,yn), где xn = 

-2, yn = 0. Далее организуется двумерный цикл, в котором x изменяется от xn = 

-2 до xk = 2, а y изменяется от yn = 0 до yk = -2, причем hx =0,2; hy = -0,1 (от-

рицательный шаг). Внутри тела цикла организован алгоритм поиска минималь-

ного  значения  функции  при  условии  попадания  аргументов  в  заданную  олб-

ласть. 

0 

-

2 

2 

-2 

y 

x 

50 

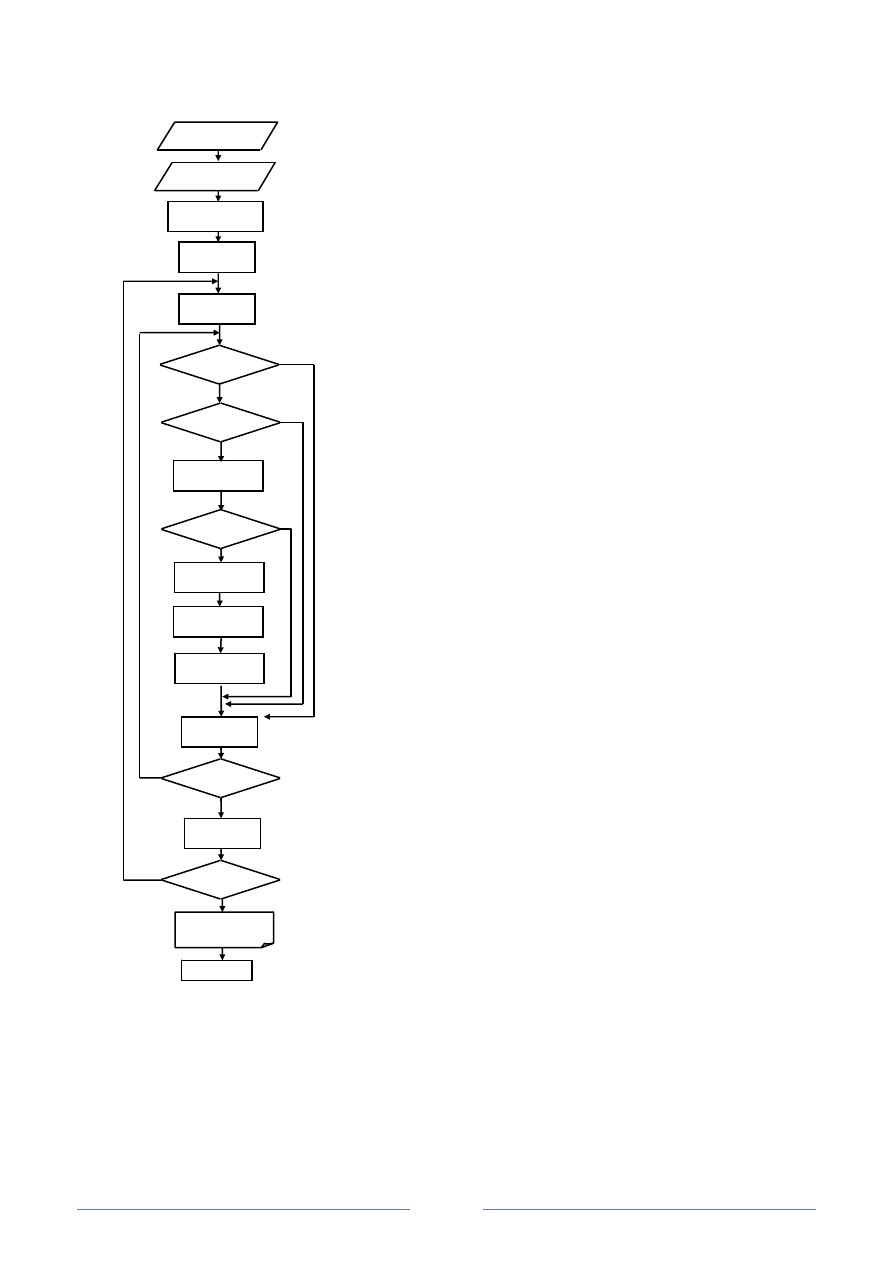
Блок-схема 

Программа на Фортране 

WRITE(*,*)’Введите xn,xk,hx’

READ(*,*) xn,xk,hx 

WRITE(*,*)’Введите yn,yk,hy’ 

READ(*,*) yn,yk,hy 

zm=f(xn,yn) 

x=xn 

10 y=yn 

5  IF (x+y.LE.-2) GOTO 1 

IF (x-y.LE.-2) GOTO 1 

z=f(x,y) 

IF (z.GE.zm) GOTO 1 

zm=z 

xm=x 

ym=y 

1 y=y+hy 

IF (y.LE.yk) GOTO 5  

x=x+hx 

IF (x.LE.xk) GOTO 10 

WRITE(*,*) xm,ym,zm 

END 

z=f(x,y

) 

x+y<-2 

y=y+hy 

x=x+hx 

y

≤ yk 

x

≤ xk 

конец 

да 

да 

нет 

нет 

нет 

да 

xn,xk,hx 

yn,yk,hy 

x=xn 

y=yn 

zm=f(xn,yn

x-y<-2 

нет 

z

≥zm 

zm=z 

xm=x 

ym=y 

xm,ym,zm 

да 

да 

нет