ВУЗ: Нижегородский государственный технический университет
Категория: Учебное пособие
Дисциплина: Информатика
Добавлен: 23.10.2018
Просмотров: 5127
Скачиваний: 18
41
Пример 3. Составить программу для решения квадратного уравнения ax
2
+ bx + c = 0. Данное уравнение имеет решение, если дискриминант D = b
2
– 4ac
не является отрицательным.
После ввода коэффициентов a, b, c вычисляется D и проверяется условие
D < 0. Если условие выполняется, то выводится сообщение «нет решения». Ес-
ли условие D < 0 не выполняется, вычисляются корни по соответствующим
формулам.
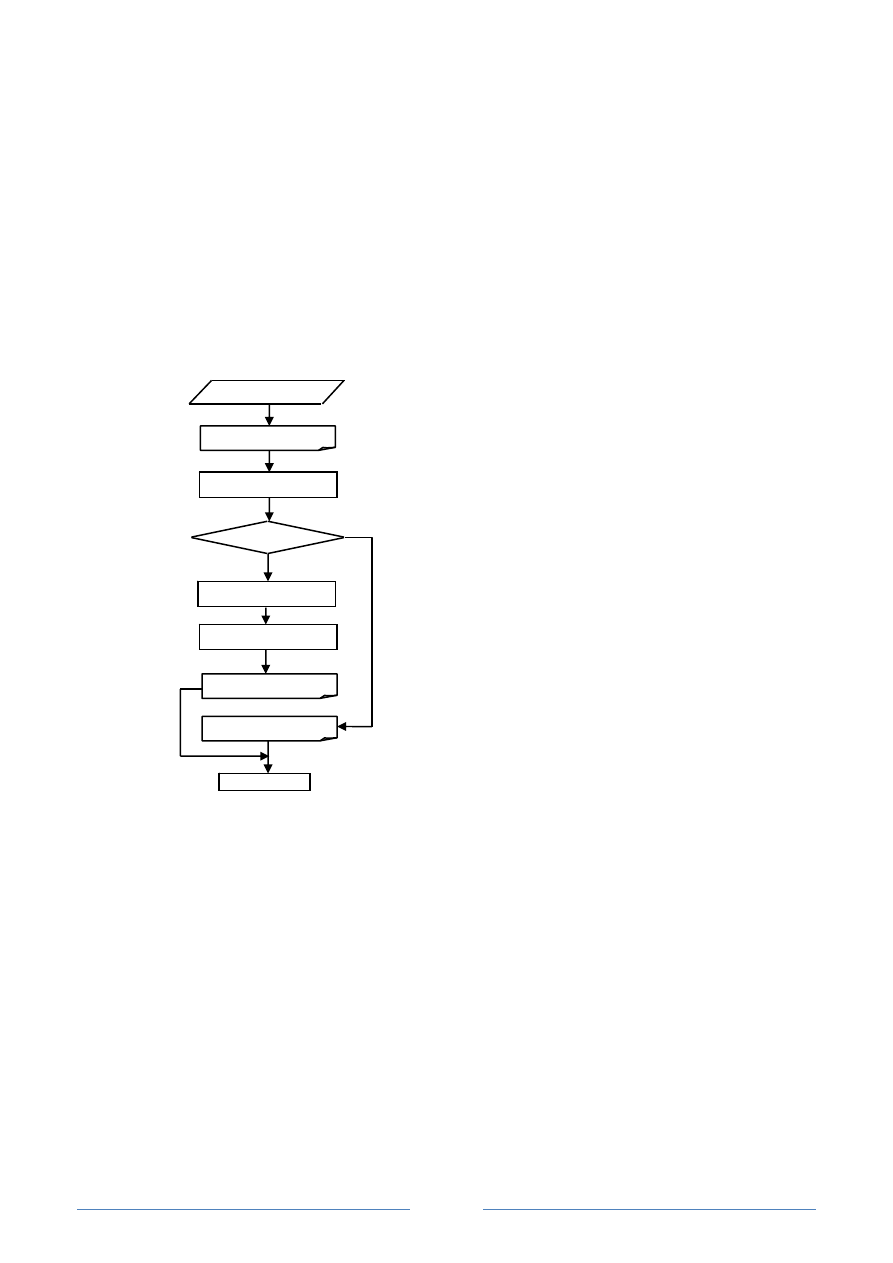
Блок-схема
Программа на Фортране
WRITE(*,*) ’Введите a,b,c’
READ(*,*) a,b.c
WRITE(*,*) ’a=’,a,’b=’,b’,c=’,c
d=b**2-4*a*c
IF (d.LT.0) GOTO 2
x1=(-b+SQRT(d))/(2*a)
x2=(-b-SQRT(d))/(2*a)
WRITE(*,*) ’x1=’,x1,’x2=’,x2
GOTO 3
2 WRITE(*,*)
’Нет решения’
3 WRITE(*,*)
END
Примечание. Поскольку оператор END не может иметь метки, перед ним
ставится пустой оператор WRITE(*,*), который приводит к простому пропуску
строки.
В данном случае, в отличие от предыдущих примеров, сначала вычисля-
ется значение переменной d, зависящее от входных параметров. Затем, в зави-
симости от знака d, алгоритм разветвляется на две ветки: одна – линейный ал-
горитм с печатью на конце, вторая – один блок печати.
Алгоритм, в котором в зависимости от условия возможны два пути про-
должения вычислительного процесса, называется простым разветвляющимся
a,b,c
d<0
x
2
=(-b-d
1/2
)/2a
x
1
=(-b+d
1/2
)/2a
конец
да
нет
x
1
, x
2
d=b
2
-4ac
a,b,c
‘Нет решения’

42
алгоритмом. Алгоритм, в котором в зависимости от выполнения условий воз-
можны несколько путей продолжения вычислительного процесса, называется
многоразветвляющимся алгоритмом.
Для программирования сложных разветвлений целесообразно использо-
вать составной оператор IF. В этом случае применяется стиль структурного
программирования, программа становится более компактной, хотя и не соот-
ветствует классической блок-схеме.
Составной оператор IF-ELSEIF-ELSE-END IF
Структура оператора:
IF(A¤B) THEN
оператор 1
ELSEIF(C¤D) THEN
оператор 2
ELSEIF(E¤F) THEN
оператор 3
ELSE
оператор k
END IF
Если условие (A¤B) выполняется, то выполняется оператор 1, и управле-
ние передается на конец конструкции (END IF). Иначе, если (ELSEIF) выполня-
ется условие (C¤D), то выполняется оператор 2, управление передается на END
IF. Если нет, то проверяется следующее условие и т.д. (ELSEIF может быть не-
сколько). Если ни одно из условий не выполнено (ELSE), то выполняется опе-
ратор k.
Структура ELSEIF может вообще отсутствовать, тогда оператор прини-
мает более простой вид:
IF(A¤B) THEN
оператор 1
ELSE
оператор 2
END IF
43
Пример. Вычислить значение функции
⎪
⎩
⎪
⎨
⎧
>
≤
≤
+
<
+
+
=
1
если
,
1
0
если
,
;
0
если
,
2
x
x
x
c
bx
x
c
bx
x
y
;
при любых заданных значениях x ,b ,c.
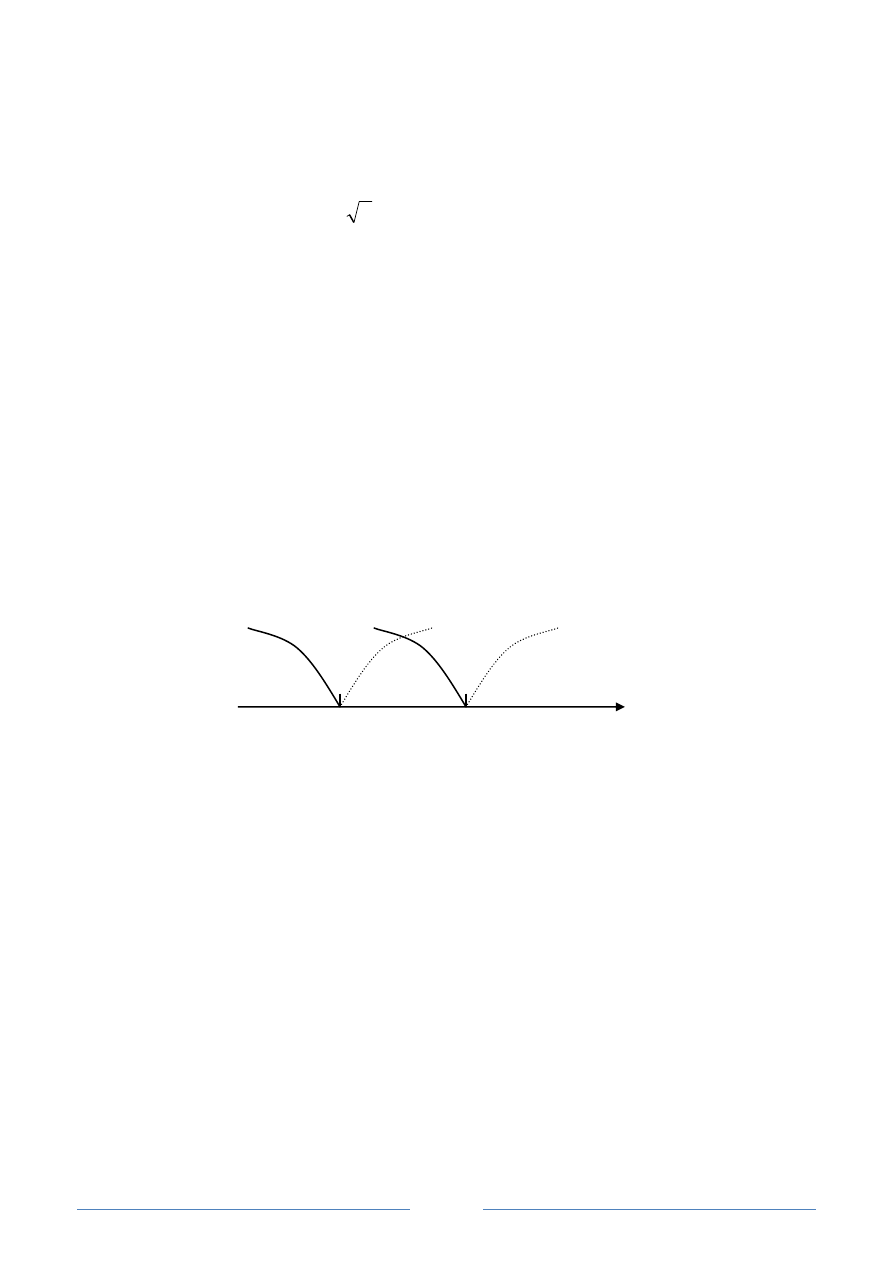
Перед решением задачи целесообразно нарисовать ось x и отложить на
ней точки ветвления (рис. 8.). Блоки условного перехода расставляем в порядке
расположения точек ветвления и в том же количестве. Проверяемые условия
обычно имеют знаки «меньше» или «меньше или равно». Первое проверяемое
условие в данном случае x < 0. Если оно не выполнено, вычисление проводится
по первой формуле, не имеет смысла проверять обратное условие. Второе про-
веряемое условие - x
≤ 1. Если оно выполнено, то вычисление осуществляется
по второй формуле. Если оба условия не выполнены, то нет смысла проверять
последнее условие, а вычисление проводится по третьей формуле.
Рис. 8. Точки ветвления
После выполнения действия по одному из разветвлений вычислительный
процесс опять сводится в одно русло.
При построении многоразветвляющегося алгоритма следует пользоваться
правилом:
вначале записываются блоки разветвления, число которых на один мень-
ше, чем количество разветвлений; эти блоки содержат лишь односторонние ус-
ловия (обычно со знаками «меньше» и «меньше или равно»); двойные условия
записывать в блок-схеме и программе нельзя;
затем записываются блоки вычисления в порядке, обратном исходным
формулам;
от каждого из блоков вычисления процесс переходит к одному блоку
(обычно блоку печати), для этого после каждого блока вычисления (кроме по-
x
1
0
1 2 3
44
следнего) следует использовать безусловный переход (стрелка на блок-схеме
или оператор GOTO в программе);
число проверяемых условий всегда на единицу меньше числа разветвле-
ний.
Приведем блок-схему и два варианта программы. Первый вариант полно-
стью соответствует блок-схеме. При этом блоки вычислений записываются в
обратном порядке, а возвращение вычислительного процесса в единое русло (к
блоку печати результатов) осуществляется с помощью оператора безусловного
перехода GOTO. Более рациональной является запись программы с использо-
ванием структурного оператора IF (второй вариант).
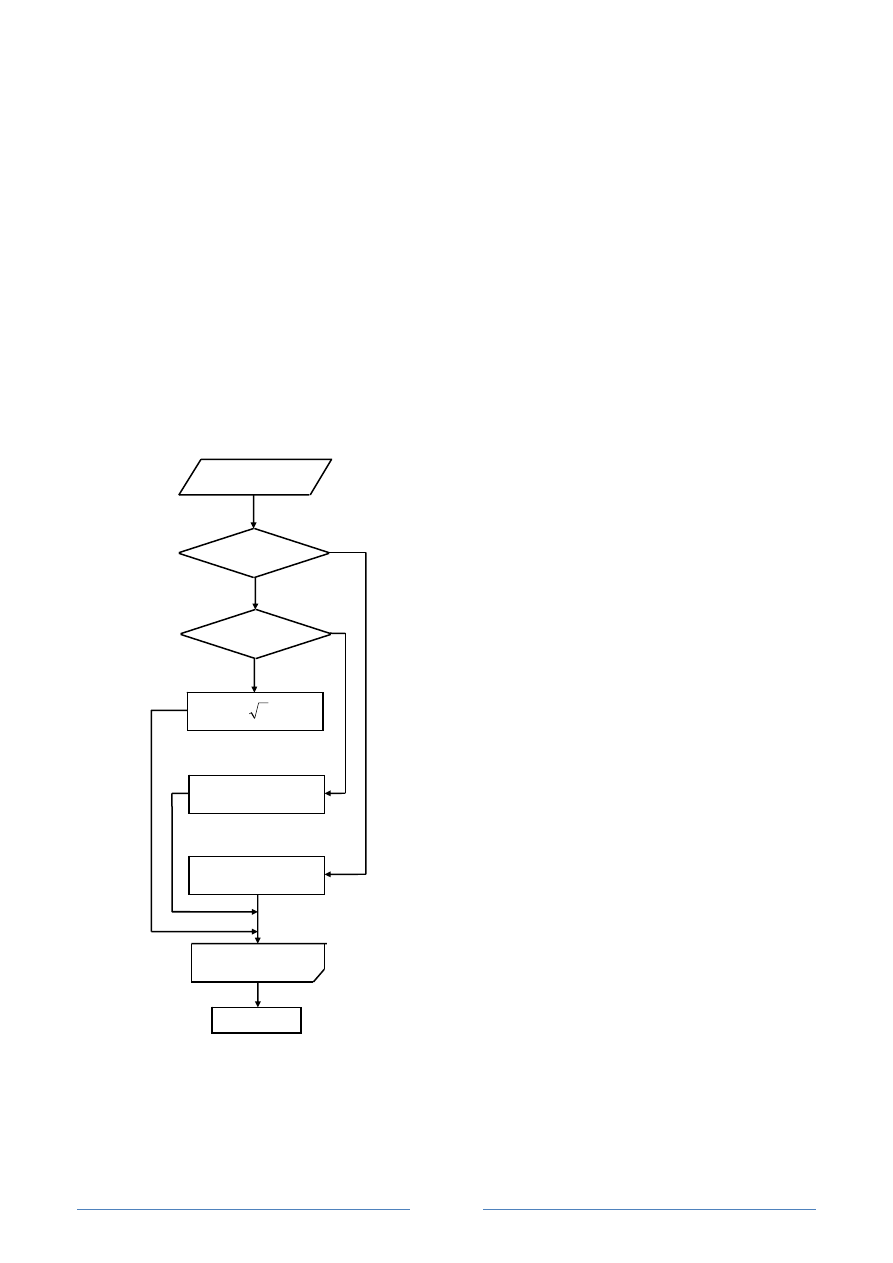
Блок-схема
Программа на Фортране
Первый вариант
WRITE(*,*) ’Введите b,c,x’
READ(*,*) b,c,x
IF (x.LT.0) GOTO 1
IF (x.LE.1) GOTO 2
y=SQRT(x)
GOTO 3
2 y=b*x+c
GOTO 3
1 y=x**2+b*x+c
3 WRITE(*,*)
’b=’,b,’c=’,c,’x=’,x,’y=’,y
END
Второй вариант
WRITE(*,*) ’Введите b,c,x’
READ(*,*) b,c,x
IF (x.LT.0) THEN
y=x**2+b*x+c
ELSE IF (x.LE.1) THEN
y=b*x+c
ELSE
y=SQRT(x)
END IF
WRITE(*,*)
’b=’,b,’c=’,c,’x=’,x,’y=’,y
END
b,c,x
x < 0
x
≤
1
y=bx+c
y=x2+bx+c
y=
9
x
b,c,x,y
конец
да
да
нет
нет

45
Циклический алгоритм
Циклическим алгоритмом называется алгоритм, часть которого выполня-
ется многократно с различными значениями изменяющейся по определенному
закону переменной (переменной цикла). На рис. 9 приведена обобщенная схема
циклического алгоритма.
Рис. 9. Обобщенная схема циклического алгоритма
Для организации цикла определяются переменная цикла (x) и его пара-
метры - начальное и конечное значение переменной цикла и шаг ее изменения
(xn, xk, hx). Блоки 1 – 4 называются блоками организации цикла:
1.
Блок начального присвоения (переменной цикла присваивается начальное
значение).
2.
Тело цикла - многократно повторяющаяся часть алгоритма, внутри кото-
рой переменная цикла не изменяется. Телом цикла может быть любой ал-
горитм: линейный, разветвляющийся или циклический.
3.
Блок приращения значения переменной цикла (переменная цикла изменя-
ет свое значение на величину шага).
4.
Блок проверки условия продолжения цикла (цикл выполняется до тех
пор, пока значение переменной цикла не превысит xk).
x=xn
Тело цикла
x=x+hx
x
≤xk
нет
да
1
2
3
4