Добавлен: 23.10.2018
Просмотров: 1659
Скачиваний: 14
-
использования планов большой размерности (т. е. с большим количеством варьируемых переменных);
-
задания ограничений сложного вида;
-
отыскания оптимального из допустимых решений;
-
генерирования множества различных решений, сохраняемых в дальнейшем в виде сценариев;
-
автоматического создания отчета по решению задачи.
Теоретической основой надстройки «Поиск решения» является симплекс-метод, позволяющий находить оптимальное решение задачи планирования с помощью итерационного процесса перехода к улучшающимся планам. В качестве примера рассмотрим решение следующей задачи.
Задача 1.Для откорма животных на ферме в их ежедневный рацион необходимо включить не менее 33 единиц питательного вещества А, 23 единиц вещества В и 12 единиц вещества С. Для откорма используется 3 вида кормов. Данные о содержании питательных веществ и стоимости весовой единицы каждого корма даны в таблице 1.
Таблица 1
-
А
В
С
Стоимость
Весовая единица корма I
4 ед.
3 ед.
1 ед.
20 к.
Весовая единица корма II
3 ед.
2 ед.
1 ед.
20 к.
Весовая единица корма III
2 ед.
1 ед.
2 ед.
10 к.
Требуется составить наиболее дешёвый рацион, при котором каждое животное получило бы необходимые количества питательных веществ А, В и С.
Решение. Пусть х1, х2, х3 – количества кормов I, II, III видов, включаемые в ежедневный рацион (хi0, i=1, 2, 3). Тогда должно быть:
![]() (1)
(1)
При этом линейная функция (стоимость рациона)
f=20х1+20х2+10х3min. (2)
Для нахождения решения этой задачи напишем программу на языке макрокоманд. Так как любая программа требует отладки, будем проводить её посредствам сравнения получающихся в процессе написания программы результатов с образцами, представленными в виде рисунков.
1. Включение компьютера и вход в систему. Результат выполнения представлен на рисунке 1.
Рис. 1.
2 .
Запуск
программы Microsoft
Excel.
.
Запуск
программы Microsoft
Excel.
Параметры: - рабочий стол. Результат выполнения представлен на рисунке 2.
Рис. 2.
3 .
Выбор
активного листа.
.
Выбор
активного листа.
Параметры: - лист: «Лист1». Результат выполнения представлен на рисунке 3.
Рис. 3.
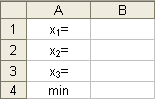
4. Занесение заголовка в ячейку.
Параметры: - ячейка: A1, A2, A3, A4; - данные: «x1=», «x2=», «x3=», «min». Результат выполнения частично представлен на рисунке 4. Рис. 4.
5. Занесение формул в ячейку.
П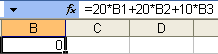 араметры:
- ячейка:
B4;
- данные:
«=20*B1+20*B2+10*B3». Результат выполнения
представлен на рисунке 5. Рис.
5.
араметры:
- ячейка:
B4;
- данные:
«=20*B1+20*B2+10*B3». Результат выполнения
представлен на рисунке 5. Рис.
5.
6 .
Занесение
заголовка в ячейку.
.
Занесение
заголовка в ячейку.
Параметры: - ячейка: A6; - данные: «Ограничения». Результат выполнения частично представлен на рисунке 6. Рис. 6.
7. Занесение формул в ячейку.
П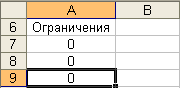 араметры:
- ячейка:
A7,
A8,
A9;
- данные:
«=4*B1+3*B2+2*B3», «=3*B1+2*B2+B3», «=B1+B2+2*B3». Результат
выполнения представлен на рисунке 7.
Рис. 7.
араметры:
- ячейка:
A7,
A8,
A9;
- данные:
«=4*B1+3*B2+2*B3», «=3*B1+2*B2+B3», «=B1+B2+2*B3». Результат
выполнения представлен на рисунке 7.
Рис. 7.
8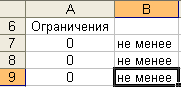 .
Занесение
заголовка в ячейку.
.
Занесение
заголовка в ячейку.
Параметры: - ячейка: B7, B8, B9; - данные: «не менее», «не менее», « не менее». Результат выполнения частично представлен на рисунке 8. Рис. 8.
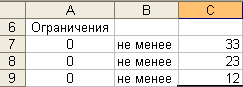
9. Занесение целых чисел в ячейку.
Параметры: - ячейка: С7, С8, С9; - данные: «33», «23», «12». Результат выполнения представлен на рисунке 9. Рис. 9.
10. Надстройка Поиск Решения.
Параметры: - целевая функция: «B4»; - равенство: «минимальное значение»; - изменяемые ячейки: «B1:B3»; - ограничения: «$A$7 >= $C$7», «$A$8 >= $C$8», «$A$9 >= $C$9», «$B$1:$B$3 >= 0». Результат выполнения представлен на рисунке 10.
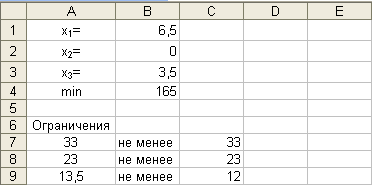
Рис. 10.
Задача 2. На товарных станциях С1 и С2 имеется по 30 комплектов мебели. Известно, что перевозка одного комплекта со станции С1 в магазины М1, М2, М3 стоит 1р., 3р., 5р., а стоимость перевозки со станции С1 в те же магазины – 2р., 5р., 4р. необходимо доставить в каждый магазин по 20 комплектов мебели. Составить план перевозок так, чтобы затраты на транспортировку мебели были наименьшими.
Решение. Количество комплектов мебели, перевозимых со станции С1 в магазины М1, М2, М3 обозначим через х1, х2, х3, а со станции С2 – через х4, х5, х6. Тогда схема перевозок буде выглядеть следующим образом:
Таблица 2
-
В М1
В М2
В М3
Всего
отправлено
Из С1
х1,
х2
х3
30
Из С2
х4
х5
х6
30
Всего получено
20
20
20
60
В соответствии с условием задачи хi0 (i=1, 2, …, 6). Задача сводится к тому, чтобы найти такое неотрицательное решение системы (3)
![]() (3)
(3)
при котором линейная функция (стоимость перевозок)
![]() (4)
(4)
имеет наименьшее значение.
Для нахождения решения этой задачи продолжим написание программы на языке макрокоманд. Так как любая программа требует отладки, будем проводить её посредствам сравнения получающихся в процессе написания программы результатов с образцами, представленными в виде рисунков.
11. Занесение заголовка в ячейку.
П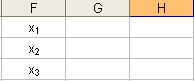 араметры:
- ячейка:
F1,
F2,
F3,
F4,
F5,
F6,
F7,
F9;
- данные:
«x1»,
«x2»,
«x3»,
«x4»,
«x5»,
«x6»,
«min»,
«Ограничения». Результат выполнения
частично представлен на рисунке 11.
Рис.
11.
араметры:
- ячейка:
F1,
F2,
F3,
F4,
F5,
F6,
F7,
F9;
- данные:
«x1»,
«x2»,
«x3»,
«x4»,
«x5»,
«x6»,
«min»,
«Ограничения». Результат выполнения
частично представлен на рисунке 11.
Рис.
11.
1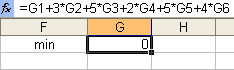 2.
Занесение формул в ячейку.
2.
Занесение формул в ячейку.
Параметры: - ячейка: G7; - данные: «=G1+3*G2+5*G3+2*G4+5*G5+4*G6». Результат выполнения представлен на рисунке 12. Рис. 12.
13. Занесение формул в ячейку.
П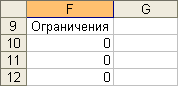 араметры:
- ячейка:
F10,
F11,
F12,
F13,
F14;
- данные:
«=G1+G2+G3», «=G4+G5+G6», «=G1+G4», «=G2+G5», «=G3+G6».
Результат выполнения частично представлен
на рисунке 13. Рис. 13.
араметры:
- ячейка:
F10,
F11,
F12,
F13,
F14;
- данные:
«=G1+G2+G3», «=G4+G5+G6», «=G1+G4», «=G2+G5», «=G3+G6».
Результат выполнения частично представлен
на рисунке 13. Рис. 13.
1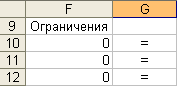 4.
Занесение
заголовка в ячейку.
4.
Занесение
заголовка в ячейку.
Параметры: - ячейка: G10, G11, G12, G13, G14; - данные: «=», «=», «=», «=», «=». Результат выполнения частично представлен на рисунке 14. Рис. 14.
1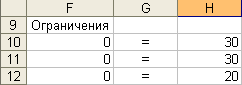 5.
Занесение целых чисел в ячейку.
5.
Занесение целых чисел в ячейку.
Параметры: - ячейка: H10, H11, H12, H13, H14; - данные: «30», «30», «20», «20», «20». Результат выполнения представлен на рисунке 15. Рис. 15.
16. Надстройка Поиск Решения.
Параметры: - целевая функция: «G7»; - равенство: «минимальное значение»; - изменяемые ячейки: «G1:G6»; - ограничения: «$F$10 = $H$10», «$F$11 = $H$11», «$F$12 = $H$12», «$F$13 = $H$13», «$F$14 = $H$14», «$G$1:$G$6 >= 0». Результат выполнения представлен на рисунке 16.
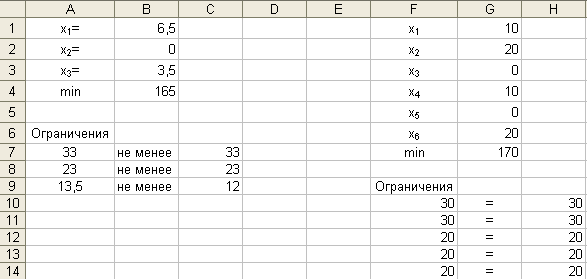
Рис. 16.
Задания для самостоятельной работы.
Задача №1. Для участия в командных соревнованиях по лёгкой атлетике спортклуб должен выставить команду, состоящую из спортсменов I и II разрядов. Соревнования проводятся по бегу, прыжкам в высоту и прыжкам в длину. В беге должны участвовать 5 спортсменов, в прыжках в длину – 8 спортсменов, в прыжках в высоту – не более 10. Количество очков, гарантируемое спортсмену каждого разряда по каждому виду, указано в таблице:
|
Разряд |
Бег |
Прыжки в высоту |
Прыжки в длину |
|
I |
4 |
5 |
5 |
|
II |
2 |
3 |
3 |
Распределить спортсменов команды так, чтобы сумма очков команды была наибольшей, если известно, что в команде I разряд имеют только 10 спортсменов.
Задача №2. Три завода производят одно и то же изделие, которое отправляется четырем потребителям. Известно, что I завод поставляет 90 вагонов изделий, II – 30 вагонов, III
– 40 вагонов. Для потребителей требуется: первому – 70 вагонов, второму – 30, третьему – 20 и четвёртому – 40. Стоимость (в руб.) перевозки одного вагона между каждым поставщиком и потребителем указаны в следующей таблице:
|
Поставщики |
1 |
2 |
3 |
4 |
|
I |
18 |
20 |
14 |
10 |
|
II |
10 |
20 |
40 |
30 |
|
III |
16 |
22 |
10 |
20 |
Определить минимальный по стоимости план перевозок.
Задача №3. Груз, хранящийся на складах, в каждом соответственно 60, 80 и 106 машин, требуется перевезти в четыре магазина. В первый магазин требуется 44 машины, во второй – 70, в третий – 50, в четвёртый – 82. Стоимость прогона одной машины за 1 км составляет 10 коп. расстояния между складами и магазинами указаны в таблице:
|
Склады |
1 |
2 |
3 |
4 |
|
1 |
13 |
17 |
6 |
8 |
|
2 |
2 |
7 |
10 |
41 |
|
3 |
12 |
18 |
2 |
22 |
Составить оптимальный по стоимости план перевозки груза из складов в магазины.
-
РЕШЕНИЕ ЗАДАЧ ОБ ОПТИМАЛЬНОМ ПЛАНИРОВАНИИ ПРОИЗВОДСТВА ПРОДУКЦИИ С ПОМОЩЬЮ СИМПЛЕКСНЫХ ТАБЛИЦ.
На практике очень часто приходится решать оптимизационные задачи, т. е. когда при наличии ряда ограничений требуется найти наилучший вариант решения. С такими задачами приходится сталкиваться менеджерам, экономистам, которые должны решать разнообразные проблемы, а именно: планирование штата сотрудников, определение фонда зарплаты, составление оптимального плана производства, планирование рекламной компании по продвижению продукции на рынок, оптимизация капиталовложений и т. д.
Эффективным инструментом при решении подобных задач является метод симплексных таблиц, позволяющий осуществить целенаправленный перебор опорных решений. Суть метода заключается в том, что математическая модель задачи сводится к ограничениям в виде системы линейных уравнений:
![]() (1)
(1)
где: b1,....,br - свободные члены; x1,....,xr – базисные переменные.
Среди неотрицательных решений системы (1) необходимо найти такие, которые максимизировали бы линейную функцию:
![]() (2)
(2)
Равенства
(1) называются приведёнными (к свободным
переменным) выражениями для функции L,
а коэффициенты
![]() -
называются оценками (индексами)
соответствующих свободных переменных
xj
.
-
называются оценками (индексами)
соответствующих свободных переменных
xj
.
Данные (1) и (2) можно представить в виде таблицы 1, которую прнято называть симплексной, т.е. простой (от simple).
Таблица 1.
Симплексная таблица
|
Базисные переменные |
Свободные переменные |
x1 |
... |
xi |
... |
xr |
xr+1 |
... |
xj |
... |
xn |
|
X1 |
B1 |
1 |
... |
0 |
... |
0 |
|
... |
|
... |
|
|
..... |
..... |
... |
... |
... |
... |
... |
... |
... |
... |
... |
... |
|
Xi |
Bi |
0 |
... |
1 |
... |
0 |
|
... |
|
... |
|
|
..... |
..... |
... |
... |
... |
... |
... |
... |
... |
... |
... |
... |
|
Xr |
br |
0 |
... |
0 |
... |
1 |
|
... |
|
... |
|
|
L |
|
0 |
... |
0 |
... |
0 |
|
... |
|
... |
|
Последовательность расчёта выглядит следующим образом:
-
Выбирают разрешающий столбец
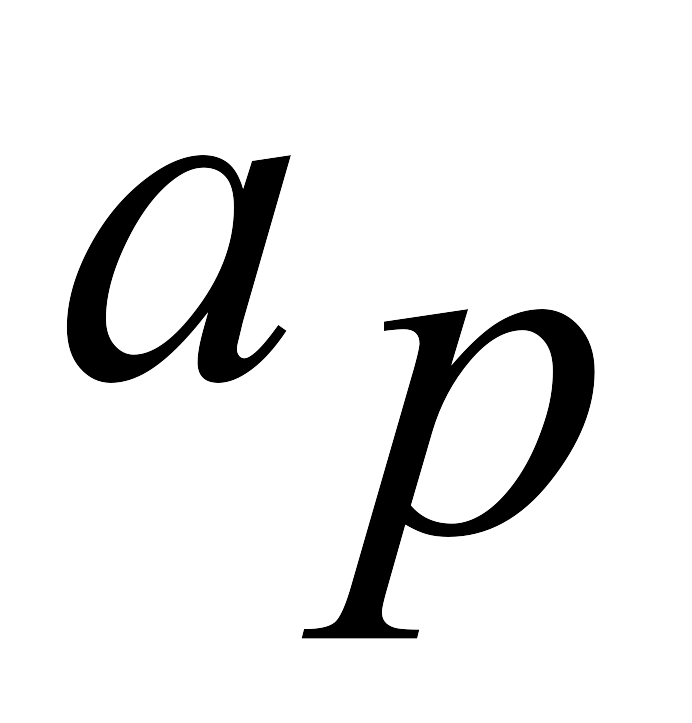 из условия:
из условия:
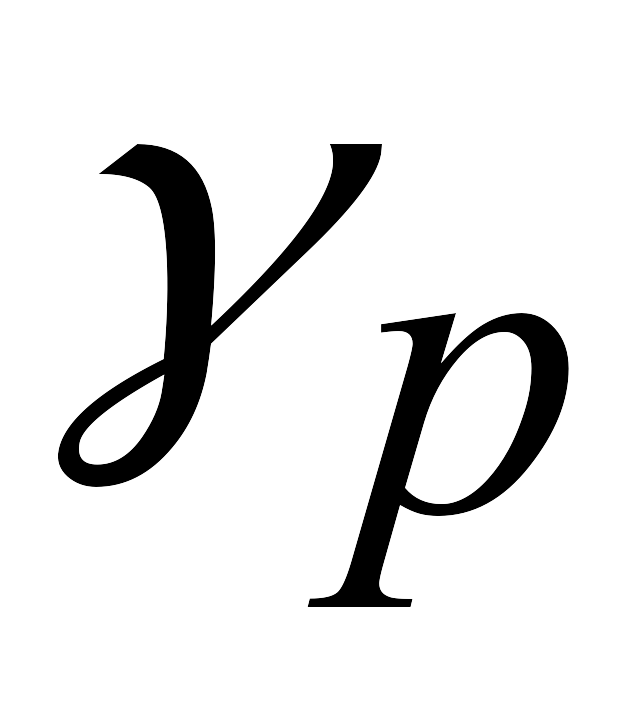 <0
и хотя бы один элемент
<0
и хотя бы один элемент
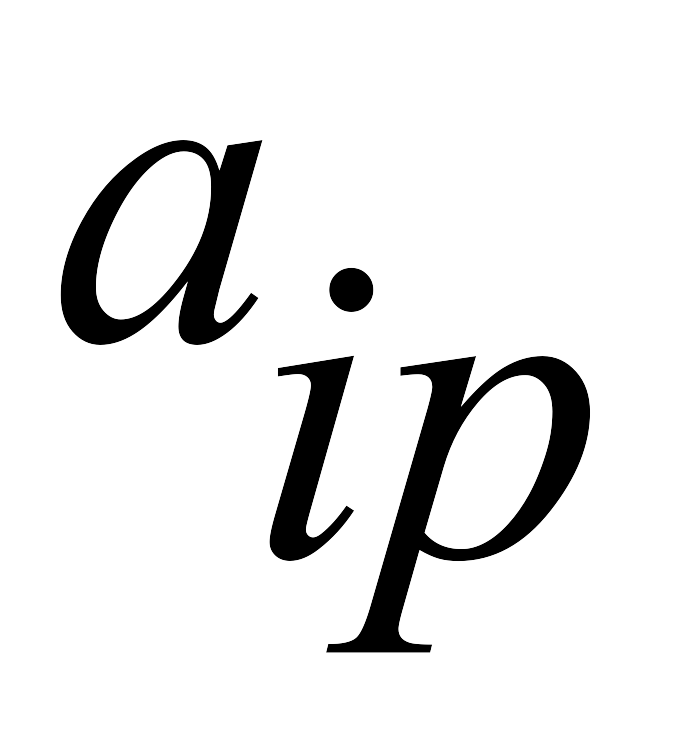 >0.
>0. -
Выбирают q- ю разрешающую строку из условия:
![]() для
для
![]() >0.
>0.
-
Производят пересчёт q-й разрешающей строки по формуле:
![]()
![]() ,
(k=0,1,2,…..,n).
,
(k=0,1,2,…..,n).
-
Вычисляют элементы всех остальных строк (при
 )
по формуле:
)
по формуле:
![]() ,
(i=0,1,....,q-1,q+1,....,r).
,
(i=0,1,....,q-1,q+1,....,r).
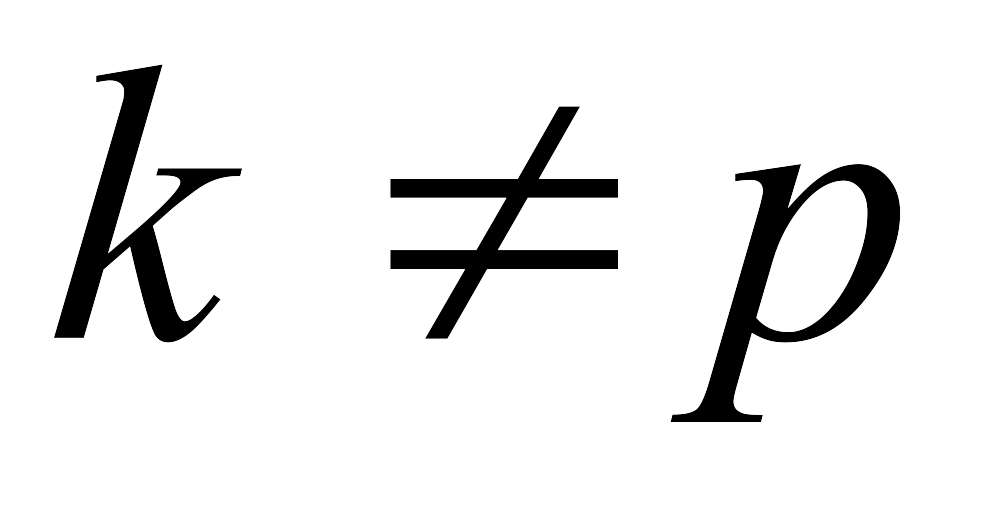
При этом, если после выполнения очередного вычисления:
-
найдётся хотя бы одна отрицательная оценка и в каждом столбце с такой оценкой окажется хотя бы один положительный элемент, т.е.
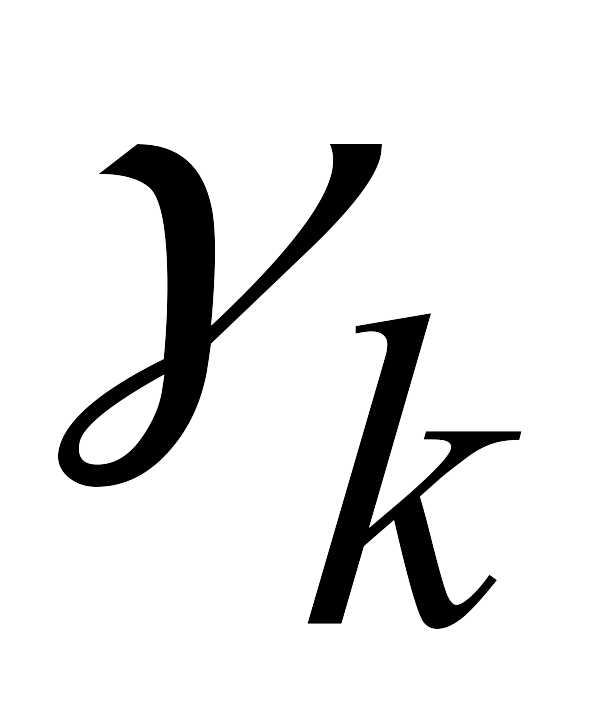 <0
для некоторых k,
и
<0
для некоторых k,
и
 >0
для тех же k
и некоторого i,
то
можно улучшить решение, выполнив
следующую итерацию по вычислению;
>0
для тех же k
и некоторого i,
то
можно улучшить решение, выполнив
следующую итерацию по вычислению; -
найдётся хотя бы одна отрицательная оценка, столбец которой не содержит положительных элементов, т.е.
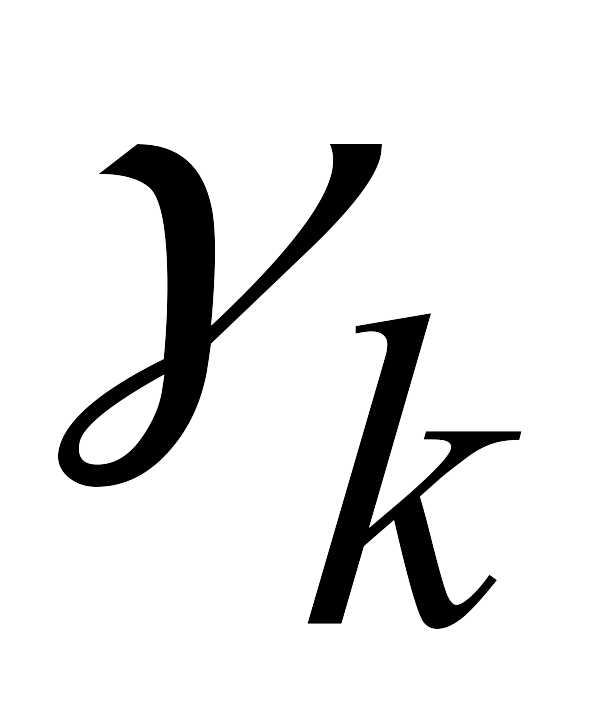 <0,
<0,
 <0,
для какого -то k
и всех i,
то
функция L
не ограничена в области допустимых
решений:
<0,
для какого -то k
и всех i,
то
функция L
не ограничена в области допустимых
решений:
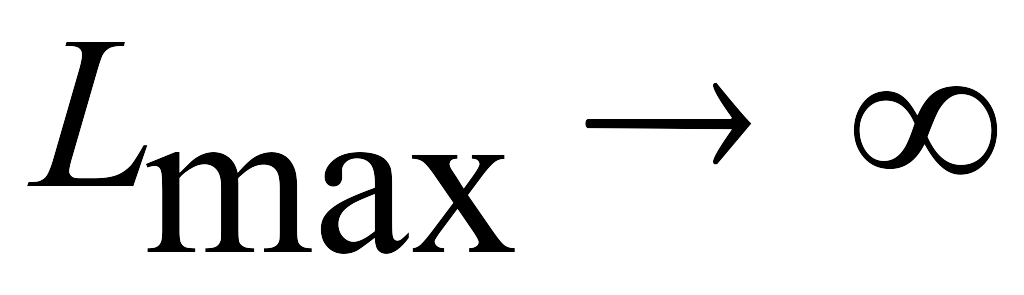 ;
; -
все оценки окажутся неотрицательными, т. е.
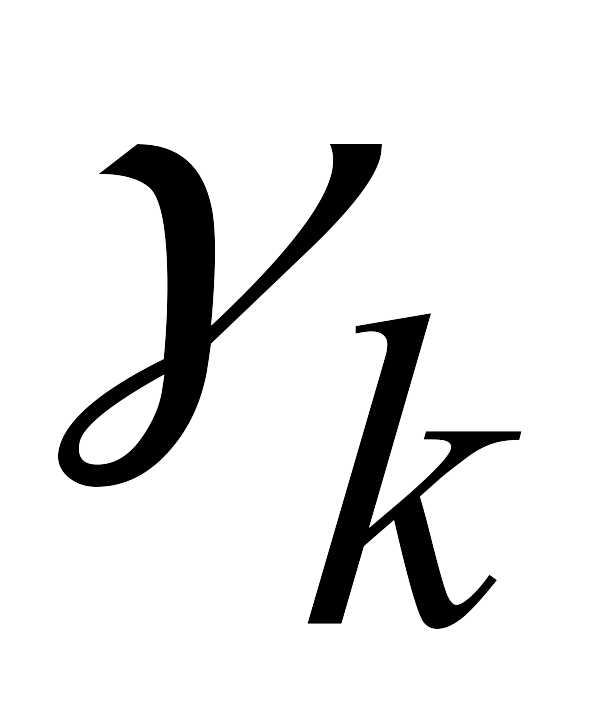
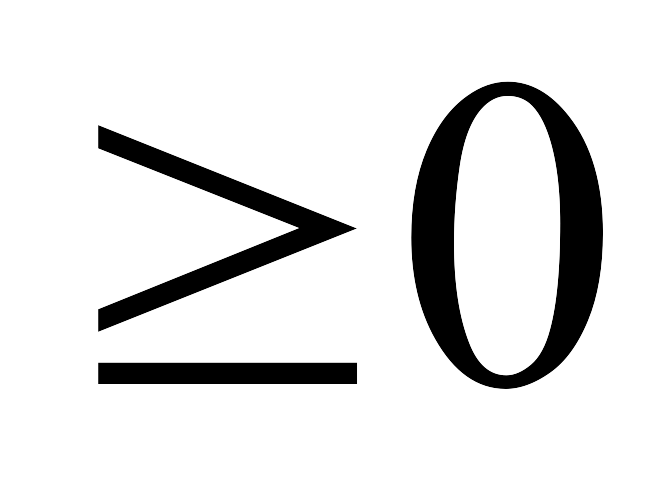 для всех k,
то
достигнуто оптимальное решение.
для всех k,
то
достигнуто оптимальное решение.
Работу метода симплексных таблиц рассмотрим в применении к задаче об оптимальном планировании производства продукции.
Кондитерская фабрика выпускает два сорта фруктовой карамели: и . Продукция фабрики отправляется на оптовую продажу. Для выработки карамели используется два вида сырья: А (сахарный песок) и В (фрукты). Складские помещения допускают максимальные суточные запасы продукции: 6 тонн для и 8 тонн для . Расходы сырья А и В на 1 тонну готовой продукции приведены в таблице 2.
Таблица2 .
Исходные данные задачи по производству карамели
|
Исходное сырьё |
Расход
исходного сырья |
Максимально возможный запас продукции на складе (в тоннах) |
|
|
Карамель |
Карамель |
||
А |
1 |
2 |
6 |
В |
2 |
1 |
8 |
Изучение рынка сбыта показало, что суточный спрос на карамель никогда не превышает спроса на карамель более чем на 1 тонну. Кроме того, установлено, что спрос на карамель никогда не превышает 2 тонн в сутки.
