Оптовые цены 1 тонны карамели равны: 30000 руб. для карамели  и 20000 руб. для карамели .

Требуется определить: какое количество карамели каждого вида должна производить кондитерская фабрика, чтобы доход от реализации продукции был максимальным ?

Для решения задачи необходимо сначала построить математическую модель, которая должна ответить на следующие вопросы:

• что является переменными модели ?

• как определяется цель, для достижения которой из множества всех допустимых значений переменных мы выбираем оптимальные ?

• каким ограничениям должны удовлетворять неизвестные ?

В нашем случае кондитерской фабрике необходимо спланировать объём производства карамели так, чтобы максимизировать прибыль. Следовательно, переменными являются:

x_ - cуточный объём производства карамели ;

x_ - cуточный объём производства карамели .

Суммарная суточная прибыль z от выработки x_ карамели  и x_ карамели  выражается следующим уравнением:

z = 30000 x_ + 20000 x_ .

Целью фабрики является определение среди всех допустимых значений x_ и x_ таких, которые максимизируют суммарную прибыль, т. е. целевую функцию z.

Определим ограничения, которые налагаются на x_ и x_ . Объём производства карамели не может быть отрицательным, следовательно:

x_ , x_  0 .

Расход исходного сырья для производства обоих видов карамели не может превосходить максимально возможный запас данного исходного продукта на складе. Таким образом, получаем систему ограничений:

x_ + 2 x_  6,

2x_ + x_  8.

Кроме того, ограничения на величину спроса на карамель имеют вид:

x_ - x_  1,

x_  2.

Итак, математическая модель рассматриваемой задачи имеет вид: максимизировать:

z = 30000 x_ + 20000 x_

при ограничениях:

x_ + 2 x_  6,

2x_ + x_  8,

x_ - x_  1,

x_  2,

x_ , x_  0.

Разработанная нами модель является линейной, т. к. целевая функция и ограничения линейно зависят от переменных.

Обозначим x_ = x₁, x_ = x₂ , z = L. Кроме того, учитывая, что ограничительные условия заданы неравенствами, введём балансовые (выравнивающие) переменные x₃, x₄, x₅, x₆. Тогда наша задача сведётся к следующей системе уравнений:

(3)

L = 20000x₁ + 30000x₂ .

Базисные переменные x₃, x₄, x₅, x₆ можно выразить через свободные переменные х₁ и х₂ и тогда система (3) примет следующий вид:

(4)

L - 20000x₁ - 30000x₂ = 0.

Используя систему (4), заполняем исходную симплексную таблицу 2.

Таблица 2.

Исходная симплексная таблица

Базисные переменные	Свободные переменные	x1	x2	x3	x4	x5	x6
x3	6	2	1	1	0	0	0
x4	8	1	2	0	1	0	0
x5	1	1	-1	0	0	1	0
x6	2	1	0	0	0	0	-1
L	0	-20000	-30000	0	0	0	0

---

1. Выясняем, есть ли в последней (индексной) строке отрицательные оценки? Таких чисел два: -20000 и –30000.

2. Выбираем наименьшее: -30000 и просматриваем столбец для х₂ . В этом столбце 2 положительных элемента: 1 и 2.

3. Делим на эти числа соответствующие свободные члены: 6/1;8/2. Выбираем нименьшее из них- это 8/2=4. Следовательно, разрещающим является элемент 2, стоящий на пересечении строки для x₄ и столбца x₂.

4. Выделим эту строку и столбец заливкой см. табл.2. Затем x₂ переводим в базисную переменную (вместо x₄). Новый базис будет состоять из переменных x₃, x₂, x₅ , x₆ .

5. Для составления следующей (2-й) симплексной таблицы делим выделенную строку табл.2 на число 2, чтобы получить на месте разрешающего элемента число 1: 8/2; ½; 2/2; 0/2; ½; 0/2;0/2. Полученную строку пишем на месте прежней.

6. К каждой из остальных строк прибавляем вновь полученную, умноженную на такое число, чтобы в клетках для столбца x₂ появились нули, и пишем преобразованные строки на месте прежних:

а)

Получено			4	1/2	1	0	1/2	0	0	)		(	-1	)	=
	=		-4	-1/2	-1	0	-1/2	0	0
		+
1-я строка из таблицы 2 :			6	2	1	1	0	0	0
			2	3/2	0	1	-1/2	0	0		1-я строка в таблицу 3

b)

Получено		(	4	1/2	1	0	1/2	0	0	)		(	1	)	=
	=		4	1/2	1	0	1/2	0	0
		+
3-я строка из таблицы 2 :			1	1	-1	0	0	1	0
			5	3/2	0	0	1/2	1	0		3-я строка в таблицу 3

с) 4-я строка: 2; 1; 0; 0; 0; 0; 1 в таблицу 3 записывается без изменения, т.к. в ней x₂ =0.

d)

Получено			(			4	1/2	1	0	1/2	0	0	)		(	30000	)	=
	=					120000	15000	30000	0	15000	0	0
			+
5-я строка из таблицы 2 				0			-20000	-30000	0	0	0	0
					120000		-5000	0	0	15000	0	0		1-я строка в таблицу 3

7. Полученные результаты заносятся в следующую симплексную

таблицу 3.

Таблица 3 .

Симплексная таблица

Базисные переменные	Свободные переменные	x1	x2	x3	x4	x5	x6
x3	2	3/2	0	1	-1/2	0	0
х2	4	1/2	1	0	1/2	0	0
x5	5	3/2	0	0	1/2	1	0
x6	2	1	0	0	0	0	-1
L	120000	-5000	0	0	15000	0	0

---

8. Выясняем, есть ли в последней (индексной) строке отрицательные оценки? Таких чисел одно: -50000.

Далее, действуя по вышеописанному алгоритму, получаем следующую симплексную таблицу 4.

Таблица 4 .

Симплексная таблица

Базисные переменные	Свободные переменные	x1	x2	x3	x4	x5	x6
х1	4/3	1	0	2/3	-1/2	0	0
х2	10/3	0	1	-1/3	1/2	0	0
x5	3	0	0	-1	1/2	1	0
x6	2/3	0	0	-2/3	0	0	-1
L	380000/3	0	0	10000/3	40000/3	0	0

Поскольку в индексной строке нет отрицательных оценок, мы получили оптимальное решение: x₁=4/3, x₂=10/3, x₃=0, x₄=0, x₅=3, x₆=2/3. При этом максимальное значение линейной функции равно:

L = 20000x₁ + 30000x₂ = 20000(4/3) +30000(10/3) = 126666,66.

Это и есть максимальный доход, исчисляемый в рублях.

Задача об оптимальном планировании производства продукции может быть решена с помощью пакета Excel. Для этого напишем программу на языке макрокоманд. Так как любая программа требует отладки, будем проводить её посредствам сравнения получающихся в процессе написания программы результатов с образцами, представленными в виде рисунков.

1. Включение компьютера и вход в систему. Результат выполнения представлен на рисунке 1.

Рис. 1.

2. Запуск программы Microsoft Excel.

Параметры: - рабочий стол. Результат выполнения представлен на рисунке 2.

Рис. 2.

3 . Выбор активного листа.

Параметры: - лист: «Лист1». Результат выполнения представлен на рисунке 3.

Рис. 3.

4 . Занесение заголовка в ячейку.

Параметры: - ячейка: A1, A2, B2; - данные: «Переменные», «x_», «x_». Результат выполнения частично представлен на рисунке 4. Рис. 4.

5 . Занесение заголовка в ячейку.

Параметры: - ячейка: A4, A6; - данные: «Функция цели», «Ограничения». Результат выполнения частично представлен на рисунке 5. Рис. 5.

6 . Занесение формул в ячейку.

Параметры: - ячейка: C4; - данные: «=30000*A3+20000*B3». Результат выполнения представлен на рисунке 6. Рис. 6.

7. Занесение формул в ячейку.

Параметры: - ячейка: A7, A8, A9, A10; - данные: «=A3+2*B3», «=2*A3+B3», «=B3-A3», «=B3». Результат выполнения представлен на рисунке 7. Рис. 7.

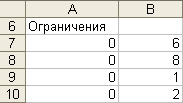
8. Занесение целых чисел в ячейку.

Параметры: - ячейка: B7, B8, B9, B10; - данные: «6», «8», «1», «2». Результат выполнения представлен на рисунке 8. Рис. 8.

9. Надстройка Поиск Решения.

Параметры: - целевая функция: «C4»; - равенство: «максимальное значение»; - изменяемые ячейки: «A3:B3»; - ограничения: «$A$3:$B$3 >= 0», «$A$7:$A$10 <= $B$7:$B$10»; - параметры: «линейная модель». Результат выполнения представлен на рисунке 9.

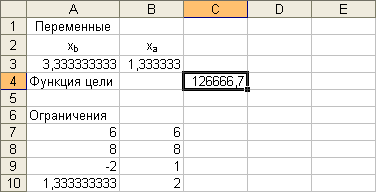
Рис. 9

Поиск решения дал оптимальный план производства карамели, дающий максимальную прибыль. Из Рис. 9 видно, что оптимальным является производство в сутки 3,333333333 тонны карамели сорта  и 1,333333333 тонны карамели сорта . Этот объём производства принесёт 126666,7 рублей прибыли.

---

Полученные материалы показывают полное совпадение результатов вычислений по методу симплексных таблиц и с помощью программного средства Excel Поиск решения. В данном случае расчёт в Excel можно рассматривать как проверочный.

Литература

1. Бубнов В.А. и др. Практические занятия по информатике. М.: «Образование Информатика», 2001. -117с.

2. Данко П.Е., Попов А.Г., Кожевникова Т.Я. Высшая математика в примерах и задачах. Часть I. М.: «Высшая школа», 1966. –304 с.

3. Медведев Т.А. Начальный курс финансовой математики. -М.: ТОО «Остожье», 2000. -267с.

4. Солодовников А.С. и др. Математика в экономике., ч. 1-3. -М.: «Финансы и статистика», -1999.

5. Курицкий Б.Я. Поиск оптимальных решений средствами Excel 7.0. –СПб.: BHV-Санкт-Петербург, 1997.-384 с.

6. Гарнаев А.Ю. Использование MS Excel и VBA в экономике и финансах. - СПб.: BHV-Санкт-Петербург, 1999.-336 с.

7. Долженков В., Колесников Ю. Microsoft Excel 2000. СПб.: BHV- Санкт-Петербург, 2001.-1088 с.

---

---

Смотрите также файлы

• Блок-схемы.docx

• Информатика Контрольная.docx

• Фрагмент БД недвижимость.doc

• Задание на контрольную работу по информатике.doc

• Курсовая работа Исследование следящей системы.pdf