Файл: Контрольная работа Математические методы теории сетей связи.pdf

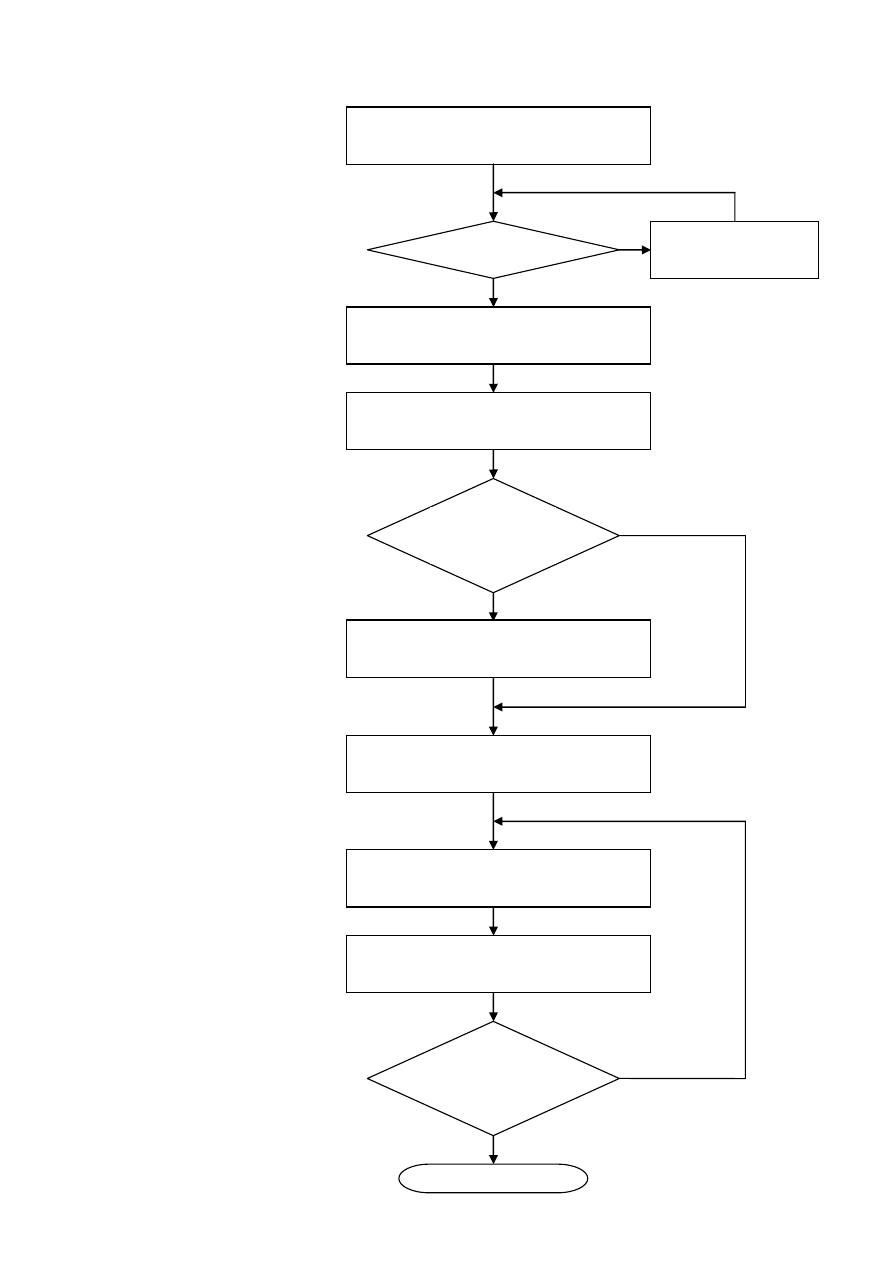
Начальные условия: 

задано n 

n=2

m

–1? 

Определение порядка корней  

неприводимых сомножителей x

n

+1 

Определение числа корней 

каждого порядка 

Корни имеют 

один порядок? 

Да 

Нет 

Вычисление степеней 

неприводимых сомножителей  

и их числа с корнями каждого порядка 

Построение циклотомических классов 

и нахождение их представителей  

Нахождение двойственных многочленов 

для неприводимых сомножителей 

Нахождение неприводимых 

сомножителей по их корням  

или по таблицам 

Все неприводимые  

сомножители найдены? 

Конец 

Да 

Нет 

Да 

Нахождение  

нового n = η 

Нет 

Шаг 10. Из таблиц приложения для степени 6 находим по представи-

телям циклотомических классов многочлены: 

3 127 В 



 х

6

+ х

4

+ х

2

+ х +1 и двойственный ему х

6

+ х

5

+х

4

+х

2

+1, 

9  015 



 х

3

+ х

2

+1 и двойственный ему х

3

+х+1, 

21 007 



 х

2

+х+1.   

Найденные  пять  неприводимых  многочленов  совместно  с  многочле-

ном х+1 представляют все неприводимые сомножители двучлена х

21

+1. 

Пример 2.5.2. Найти неприводимые сомножители х

13

+1 над GF(2). 

Шаг 1. Степень разлагаемого двучлена равна 13. 

Шаг 2. Число 13 не может быть представлено в виде 2

m

– 1. 

Шаг  3.  Ближайшее  целое  число,  большее  числа  13,  которое  может 

быть представлено в виде 2

m

– 1 и делится на 13, есть η=2

12

–1 (табл. 2.4.2). 

Шаг 4. Порядок корней двучлена х

13

+1 равен φ(13) =12. 

Шаг 5. Все корни двучлена х

13

+1 кроме корня х = 1, имеют порядок 12. 

Шаг 6. См. шаг 5. 
Шаг 7. Может быть пропущен. 
Шаг 8. Циклотомический класс по модулю 13: 

{1, 2, 4, 8, 3, 6, 12, 11, 9, 5, 10, 7}, т. е. в разложение двучлена х

13

+1 входит 

неприводимый  многочлен  степени  12,  принадлежащий  показателю  13.  По 
модулю η=2

12

–1 этому многочлену соответствует циклотомический класс 

с представителем s = (2

12

–1)/13 = 315. 

Шаг 9. Может быть пропущен. 
Шаг 10. Из таблиц приложения для степени 12 определяем, что иско-

мый многочлен – 315 17777 D. Этот результат вполне ожидаем и мог быть 
определен еще на шаге 4. 

ЗАДАНИЯ ДЛЯ ВЫПОЛНЕНИЯ 

В каждом из 6 разделов студент должен ответить на 1 вопрос или 

решить  одну  задачу,  в  зависимости  от  задания.    Студент  должен  ре-
шить в итоге 6 заданий,  которые выбирает самостоятельно из переч-
ня, приведенного в каждой теме.  
 
 
 
 

1. Основные алгебраические системы,  

используемые в теории кодирования 

Линейные коды и математический аппарат, используемый для их опи-

сания и построения. 

Группа, кольцо, поле. Примеры использования в теории кодирования. 
Подгруппы и смежные классы. 
Действия над смежными классами. 
Литература: см. 1.1 и 1.2. 
Цель.  Изучить  основные  алгебраические  системы,  используемые  в 

теории  помехоустойчивого  кодирования.  Получить  навыки  в  решении  за-
дач, связанных с понятиями группа, кольцо, поле. 

Контрольные вопросы 

1.1. Показать, что множество всех целых чисел (положительных, отри-

цательных и нуля) является группой по операциям: 

а) обычного сложения G

+

, 

б) обычного умножения G



. 

В  группе  G

+

  по  операции  сложения  выделить  подгруппу,  состоящую 

из чисел: 

а) кратных 3, 
б) кратных 4, 
в) кратных 5. 
Построить смежные классы для каждой из этих подгрупп. 
1.2.  Проверить,  обладают  ли  полученные  в  п. 1.1  смежные  классы 

групповыми свойствами: 

а) по операции сложения, 
б) по операции умножения. 
1.3. Являются ли образованные в п. 1.2 смежные классы кольцом? По-

чему? 

1.4. Являются ли образованные в п. 1.2 смежные классы полем? Почему? 
1.5. Построить все возможные двоичные последовательности длины 5. 

Являются ли они группой по операции поразрядного сложения по mod 2? 
Доказать. 

1.6.  Образовать  все  возможные  подгруппы  в  группе  двоичных  после-

довательностей длины 5 по операции, введенной в п. 1.5. 

(Рассмотреть элементы группы как вектора и воспользоваться понятием 

базиса векторного пространства. Для каждой подгруппы указать ее порядок). 

1.7. Для каждой найденной подгруппы в п. 1.6 найти подгруппу из это-

го же множества с ортогональными векторами. Ортогональности векторов 
соответствует равенство нулю их скалярного произведения. 

1.8.  Что  нужно  сделать,  чтобы  все  последовательности  длины  5  из 

п. 1.5 стали кольцом? 

1.9. Является ли кольцо из п. 1.8 полем? 
1.10.  Какие  подполя  существуют  в поле  из всех  двоичных  последова-

тельностей длины 5? 

1.11. Проверить, что элементы поля GF(2

2

) α и 1+α являются корнями 

многочлена π(х)=1+х+х

2

 в двоичном поле. 

Примеры решения задач и дополнительные задачи 

1.12. Перечислить групповые аксиомы и привести примеры по  их вы-

полнению для операций сложения и умножения. 

Решение 

I. Замкнутость: 
a, b є G; a □ b=с є G. 
II. Ассоциативность: 
(a □ b) □ c=a □ (b □ c), где a, b, c є G. 
III. Наличие единичного элемента е: 
a □ e=e □ a, где e, a є G. 
IV. Наличие обратных элементов 

a



: 

a □  a



=  a



 □ a=e, где a,  a



, e є G.   

V. Коммутативность: 
a □ b=b □ a, где a, b є G. 
VI. Дистрибутивность: 
(a + b) c=ac+bc, где a, b, c є G. 
В  I–V  □ означает  либо  +  (операция  сложения),  либо  ×  (операция  ум-

ножения). 

1.13.  Число  p  –  простое  число.  Дать  определение  простого  поля,  ука-

зать число элементов и сформировать таблицы сложения и умножения для 
р = 2 и 3. 

Решение 

а) p = 2: 
GF(2)  –  совокупность  классов  вычетов  по  mod  2,  удовлетворяющая 

групповым аксиомам по операциям сложения и умножения: 

-  замкнутость, 
-  ассоциативность, 
-  наличие единичного элемента, 
-  наличие обратных элементов, 
-  коммутативность, 
-  дистрибутивность. 

Сформируем классы вычетов: 

…  –10  –8 

–6 

–4 

–2  {0} 

2 

4 

6 

8 

10 

… 

… 

–9 

–7 

–5 

–3 

–1  {1} 

3 

5 

7 

9 

11 

… 

Поле GF(2) содержит 2 элемента 0 и 1; 0={0}, 1={1}.  

Таблицы сложения и умножения: 

+ 

0 

1 

× 

0 

1 

0 
1 

0 
1 

1 
0 

0 
1 

0 
0 

0 
1 

б) p = 3: 

GF(3) – совокупность классов вычетов по mod 3: 
 

… 

–12 

–9 

–6 

–3 

{0} 

3 

6 

9 

12 

… 

… 

–11 

–8 

–5 

–2 

{1} 

4 

7 

10 

13 

… 

… 

–10 

–7 

–4 

–1 

{2} 

5 

8 

11 

14 

… 

Классы  вычетов  удовлетворяют  групповым  аксиомам  по  операциям 

сложения и умножения (см. п. а) 

Поле содержит 3 элемента 0, 1, 2; 0 ={0}, 1={1}=1, 2={2}.  

Таблицы сложения и умножения: 

+ 

0 

1 

2 

× 

0 

1 

2 

0 
1 
2 

0 
1 
2 

1 
2 
0 

2 
0 
1 

0 
1 
2 

0 
0 
0 

0 
1 
2 

0 
2 
1 

1.14. Задана совокупность всех двоичных последовательностей длины 3:  

000 , 001 , 010 , 011 , 100 , 101 , 110 , 111. Найти последовательности, орто-
гональные каждой из перечисленных. 

Решение 

Последовательности  ортогональны,  если  их  скалярное  произведение 

равно 0. 

Умножение двоичных последовательностей выполняется по правилам 

скалярного произведения векторов над двоичным полем, т.е. с использова-
нием таблиц сложения и умножения по mod 2. 

000 – ортогональна всем последовательностям,  

так как (000)×(е

1

е

2

е

3

) = 0×е

1

+ 0×е

2

 + 0×е

3

 = 0 для  любого е

i

= 0 или 1. 

001 – ортогональна всем последовательностям, содержащим 0 в край-

нем справа разряде: 000, 100, 010, 110. 

010 –  ортогональна  всем последовательностям, содержащим 0  в  сред-

нем разряде: 000, 001, 100, 101. 

011 – ортогональна всем последовательностям, содержащим только ну-

ли или только единицы в двух крайних справа разрядах: 000, 011, 100, 111.