Файл: Лекция 9. Системы распознавания образов (идентификации). Нейронные сети.doc

Другой алгоритм обучения без учителя – алгоритм Кохонена – предусматривает подстройку синапсов на основании их значений от предыдущей итерации.

(3)

Из вышеприведенной формулы видно, что обучение сводится к минимизации разницы между входными сигналами нейрона, поступающими с выходов нейронов предыдущего слоя y_i^(n‑1), и весовыми коэффициентами его синапсов.

Полный алгоритм обучения имеет примерно такую же структуру, как в методах Хебба, но на шаге 3 из всего слоя выбирается нейрон, значения синапсов которого максимально походят на входной образ, и подстройка весов по формуле (3) проводится только для него. Эта, так называемая, аккре­ди­тация может сопровождаться затормаживанием всех остальных нейронов слоя и введе­нием выбранного нейрона в насыщение. Выбор такого нейрона может осуществляться, например, рас­че­том скалярного произведения вектора весовых коэффициентов с вектором входных значе­ний. Максимальное произведение дает выигравший нейрон.

Другой вариант – расчет расстояния между этими векторами в p-мерном пространстве, где p – размер векторов.

, (4)

где j – индекс нейрона в слое n, i – индекс суммирования по нейронам слоя (n-1), w_ij – вес синапса, соединяющего нейроны; выходы нейронов слоя (n-1) являются входными значениями для слоя n. Корень в формуле (4) брать не обязательно, так как важна лишь относительная оценка различных D_j.

В данном случае, "побеждает" нейрон с наименьшим расстоянием. Иногда слишком часто получающие аккредитацию нейроны принудительно исключаются из рассмотрения, чтобы "урав­нять права" всех нейронов слоя. Простейший вариант такого алгоритма заключается в торможении только что выигравшего нейрона.

При использовании обучения по алгоритму Кохонена существует практика нормализации входных образов, а так же – на стадии инициализации – и нормализации начальных значений весовых коэффициентов.

, (5)

где x_i – i-ая компонента вектора входного образа или вектора весовых коэффициентов, а n – его размерность. Это позволяет сократить длительность процесса обучения.

Инициализация весовых коэффициентов случайными значениями может привести к тому, что различные классы, которым соответствуют плотно распределенные входные образы, сольются или, наоборот, раздробятся на дополнительные подклассы в случае близких образов одного и того же класса. Для избежания такой ситуации используется метод выпуклой комбинации[3]. Суть его сводится к тому, что входные нормализованные образы подвергаются преобразованию:

, (6)

где x_i – i-ая компонента входного образа, n – общее число его компонент, (t) – коэф­фи­ци­ент, изменяющийся в процессе обучения от нуля до единицы, в результате чего вначале на входы сети подаются практически одинаковые образы, а с течением времени они все больше сходятся к исходным. Весовые коэффициенты устанавливаются на шаге инициализации равными величине

, (7)

где n – размерность вектора весов для нейронов инициализируемого слоя.

На основе рассмотренного выше метода строятся нейронные сети особого типа – так назы­ва­емые самоорганизующиеся структуры – self-organizing feature maps (этот устоявшийся перевод с английского, на мой взгляд, не очень удачен, так как, речь идет не об изменении структуры сети, а только о подстройке синапсов). Для них после выбора из слоя n нейрона j с минимальным расстоянием D_j (4) обучается по формуле (3) не только этот нейрон, но и его соседи, расположенные в окрестности R. Величина R на первых итерациях очень большая, так что обучаются все нейроны, но с течением времени она уменьшается до нуля. Таким образом, чем ближе конец обучения, тем точнее определяется группа нейронов, отвечающих каждому классу образов.

Нейронные сети Хопфилда и Хэмминга

Среди различных конфигураций искуственных нейронных сетей (НС) встречаются такие, при классификации которых по принципу обучения, строго говоря, не подходят ни обучение с учителем, ни обучение без учителя. В таких сетях весовые коэффициенты синапсов рассчитываются только однажды перед началом функционирования сети на основе информации об обрабатываемых данных, и все обучение сети сводится именно к этому расчету. С одной стороны, предъявление априорной информации можно расценивать, как помощь учителя, но с другой – сеть фактически просто запоминает образцы до того, как на ее вход поступают реальные данные, и не может изменять свое поведение, поэтому говорить о звене обратной связи с "миром" (учителем) не приходится. Из сетей с подобной логикой работы наиболее известны сеть Хопфилда и сеть Хэмминга, которые обычно используются для организации ассоциативной памяти. Далее речь пойдет именно о них.

Структурная схема сети Хопфилда приведена на Рис. 6. Она состоит из единственного слоя нейронов, число которых является одновременно числом входов и выходов сети. Каждый нейрон связан синапсами со всеми остальными нейронами, а также имеет один входной синапс, через который осуществляется ввод сигнала. Выходные сигналы, как обычно, образуются на аксонах.

Рис. 6. Структурная схема сети Хопфилда.

Задача, решаемая данной сетью в качестве ассоциативной памяти, как правило, формулируется следующим образом. Известен некоторый набор двоичных сигналов (изображений, звуковых оцифровок, прочих данных, описывающих некие объекты или характеристики процессов), которые считаются образцовыми. Сеть должна уметь из произвольного неидеального сигнала, поданного на ее вход, выделить ("вспомнить" по частичной информации) соответствующий образец (если такой есть) или "дать заключение" о том, что входные данные не соответствуют ни одному из образцов. В общем случае, любой сигнал может быть описан вектором X = { x_i: i=0...n-1}, n – число нейронов в сети и размерность входных и выходных векторов. Каждый элемент x_i равен либо +1, либо -1. Обозначим вектор, описывающий k-ый образец, через X^k, а его компоненты, соответственно, – x_i^k, k=0...m-1, m – число образцов. Когда сеть распознáет (или "вспомнит") какой-либо образец на основе предъявленных ей данных, ее выходы будут содержать именно его, то есть Y = X^k, где Y – вектор выходных значений сети: Y = { y_i: i=0,...n-1}. В противном случае, выходной вектор не совпадет ни с одним образцовым.

Если, например, сигналы представляют собой некие изображения, то, отобразив в графи­ческом виде данные с выхода сети, можно будет увидеть картинку, полностью совпадающую с одной из образцовых (в случае успеха) или же "вольную импровизацию" сети (в случае неудачи).

На стадии инициализации сети весовые коэффициенты синапсов устанавливаются следующим образом:

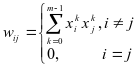(1)

Здесь i и j – индексы, соответственно, предсинаптического и постсинаптического нейронов; x_i^k, x_j^k – i-ый и j-ый элементы вектора k-ого образца.

Алгоритм функционирования сети следующий (p – номер итерации):

1. На входы сети подается неизвестный сигнал. Фактически его ввод осуществляется непо­сред­ственной установкой значений аксонов:

y_i(0) = x_i , i = 0...n-1, (2)

поэтому обозначение на схеме сети входных синапсов в явном виде носит чисто условный характер. Ноль в скобке справа от y_i означает нулевую итерацию в цикле работы сети.

2. Рассчитывается новое состояние нейронов

, j=0...n-1 (3)

и новые значения аксонов

(4)

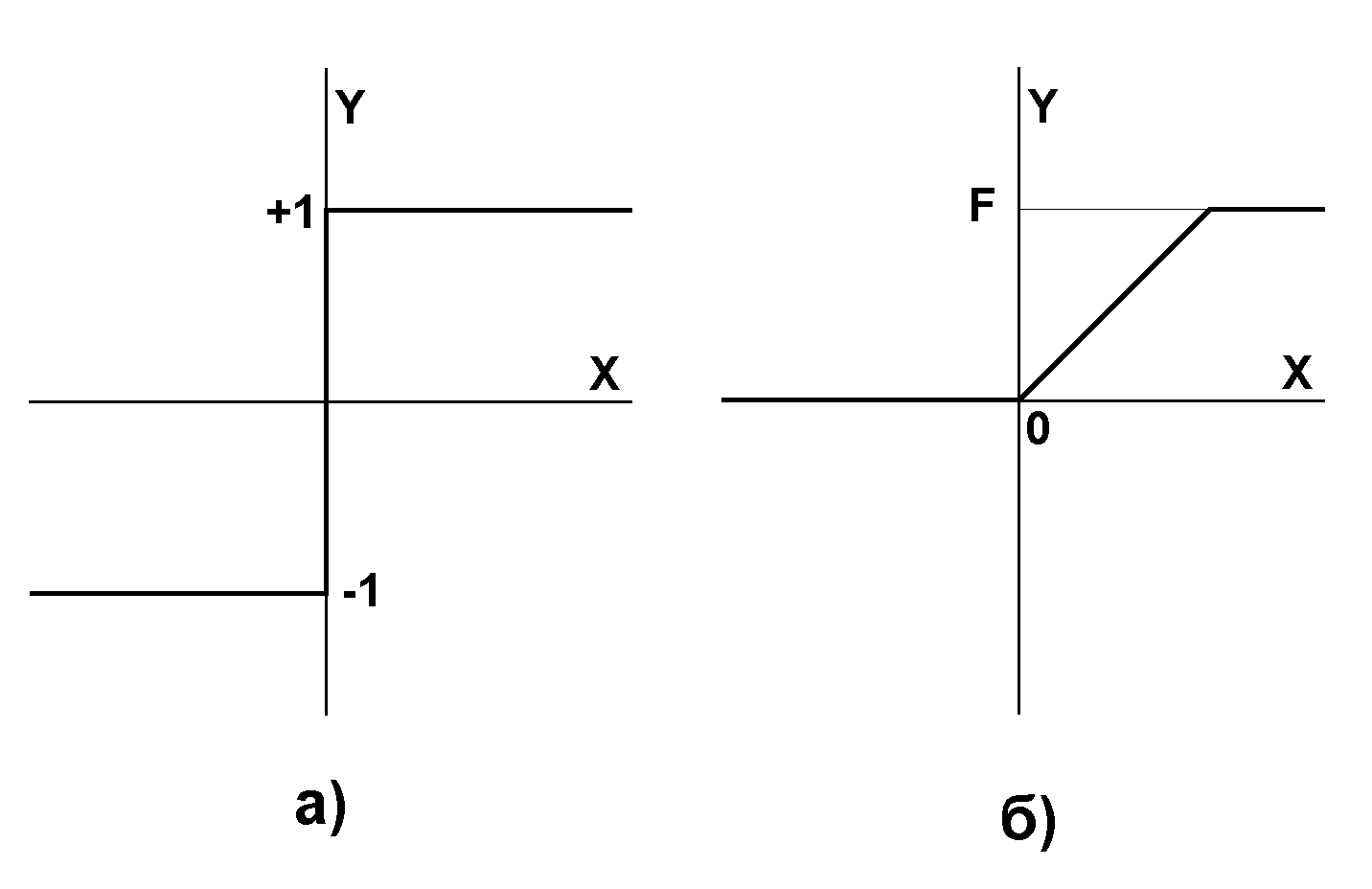
Рис. 7. Активационные функции.

3. Проверка, изменились ли выходные значения аксонов за последнюю итерацию. Если да – переход к пункту 2, иначе (если выходы застабилизировались) – конец. При этом выходной вектор представляет собой образец, наилучшим образом сочетающийся с входными данными.

Как говорилось выше, иногда сеть не может провести распознавание и выдает на выходе несуществующий образ. Это связано с проблемой ограниченности возможностей сети. Для сети Хопфилда число запоминаемых образов m не должно превышать величины, примерно равной 0.15•n. Кроме того, если два образа А и Б сильно похожи, они, возможно, будут вызывать у сети перекрестные ассоциации, то есть предъявление на входы сети вектора А приведет к появлению на ее выходах вектора Б и наоборот.

Рис. 8. Структурная схема сети Хэмминга.

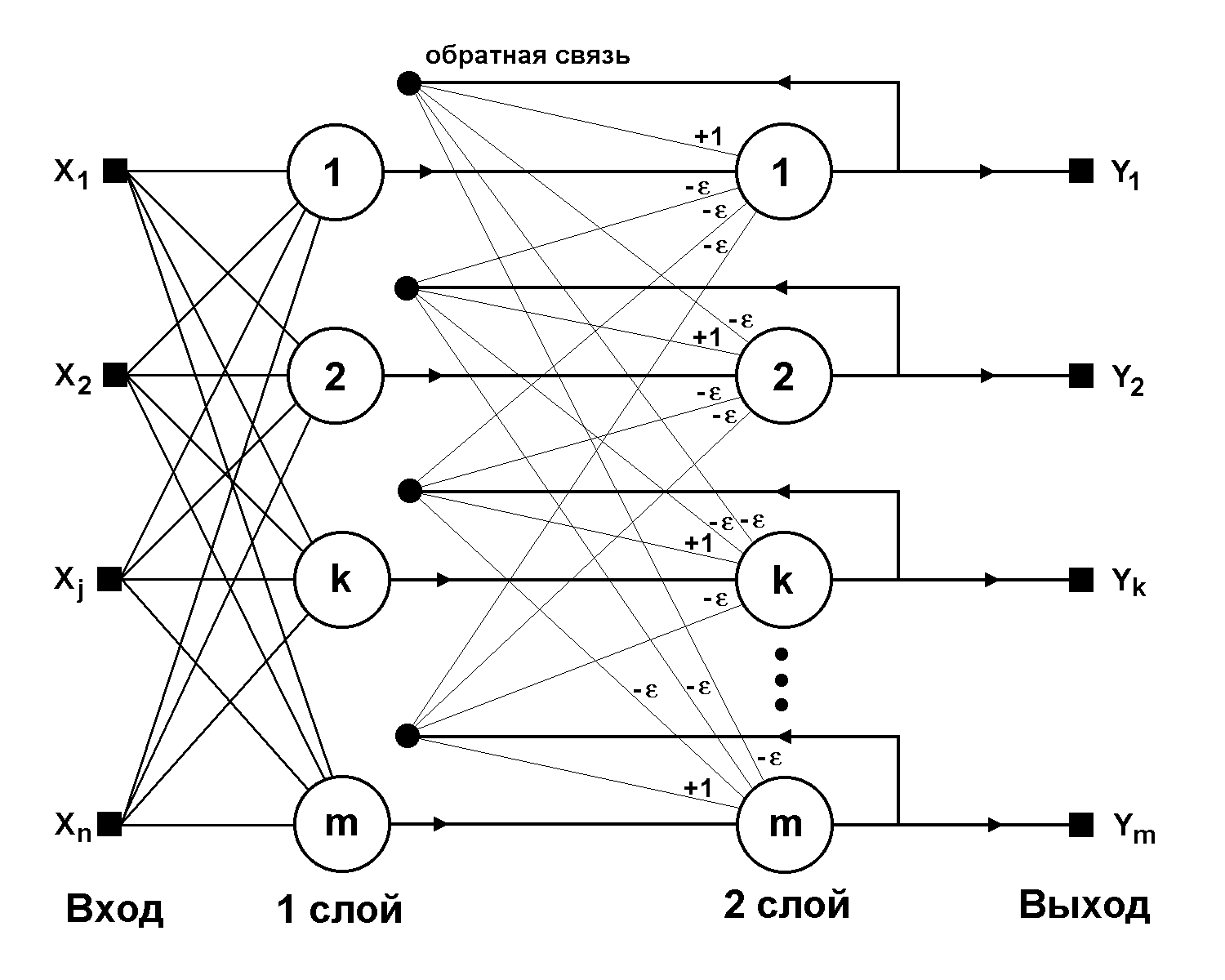
Когда нет необходимости, чтобы сеть в явном виде выдавала образец, то есть достаточно, скажем, получать номер образца, ассоциативную память успешно реализует сеть Хэмминга. Данная сеть характеризуется, по сравнению с сетью Хопфилда, меньшими затратами на память и объемом вычислений, что становится очевидным из ее структуры (Рис. 8).

Сеть состоит из двух слоев. Первый и второй слои имеют по m нейронов, где m – число образцов. Нейроны первого слоя имеют по n синапсов, соединенных со входами сети (образующими фиктивный нулевой слой). Нейроны второго слоя связаны между собой ингибиторными (отрицательными обратными) синаптическими связями. Единственный синапс с положительной обратной связью для каждого нейрона соединен с его же аксоном.

Идея работы сети состоит в нахождении расстояния Хэмминга от тестируемого образа до всех образцов. Расстоянием Хэмминга называется число отличающихся битов в двух бинарных векторах. Сеть должна выбрать образец с минимальным расстоянием Хэмминга до неизвестного входного сигнала, в результате чего будет активизирован только один выход сети, соответствующий этому образцу.

На стадии инициализации весовым коэффициентам первого слоя и порогу активационной функции присваиваются следующие значения:

, i=0...n-1, k=0...m-1 (5)

T_k = n / 2, k = 0...m-1 (6)

Здесь x_i^k – i-ый элемент k-ого образца.

Весовые коэффициенты тормозящих синапсов во втором слое берут равными некоторой величине 0 <  < 1/m. Синапс нейрона, связанный с его же аксоном имеет вес +1.

Алгоритм функционирования сети Хэмминга следующий:

1. На входы сети подается неизвестный вектор X = {x_i:i=0...n-1}, исходя из которого рассчитываются состояния нейронов первого слоя (верхний индекс в скобках указывает номер слоя):

, j=0...m-1 (7)

После этого полученными значениями инициализируются значения аксонов второго слоя:

y_j⁽²⁾ = y_j⁽¹⁾, j = 0...m-1 (8)

2. Вычислить новые состояния нейронов второго слоя:

(9)

и значения их аксонов:

(10)

Активационная функция f имеет вид порога (рис. 2б), причем величина F должна быть достаточно большой, чтобы любые возможные значения аргумента не приводили к насыщению.

3. Проверить, изменились ли выходы нейронов второго слоя за последнюю итерацию. Если да – перейди к шагу 2. Иначе – конец.

Из оценки алгоритма видно, что роль первого слоя весьма условна: воспользовавшись один раз на шаге 1 значениями его весовых коэффициентов, сеть больше не обращается к нему, поэтому первый слой может быть вообще исключен из сети (заменен на матрицу весовых коэффициентов).

Метод потенциальных функций

Предположим, что требуется разделить два непересекающихся образа V₁ и V₂. Это значит, что в пространстве изображений существует, по крайней мере, одна функция, которая полностью разделяет множества, соответствующие образам V₁ и V₂. Эта функция должна принимать положительные значения в точках, соответствующих объектам, принадлежащим образу V₁, и отрицательные — в точках образа V₂. В общем случае таких разделяющих функций может быть много, тем больше, чем компактней разделяемые множества. В процессе обучения требуется построить одну из этих функций, иногда в некотором смысле наилучшую.

Метод потенциальных функций связан со следующей процедурой. В процессе обучения с каждой точкой пространства изображений, соответствующей единичному объекту из обучающей последовательности, связывается функция U(X, X_i), заданная на всем пространстве и зависящая от X_i как от параметра. Такие функции называются потенциальными, так как они напоминают функции потенциала электрического поля вокруг точечного электрического заряда. Изменение потенциала электрического поля по мере удаления от заряда обратно пропорционально квадрату расстояния. Потенциал, таким образом, может служить мерой удаления точки от заряда. Когда поле образовано несколькими зарядами, потенциал в каждой точке этого поля равен сумме потенциалов, создаваемых в этой точке каждым из зарядов. Если заряды, образующие поле, расположены компактной группой, потенциал поля будет иметь наибольшее значение внутри группы зарядов и убывать по мере удаления от нее.

Обучающей последовательности объектов соответствует последовательность векторов X₁, X₂, …, в пространстве изображений с которыми связана последовательность U(X, X₁), U(X, X₂), … потенциальных функций, используемых для построения функций f(X₁, X₂, …). По мере увеличения числа объектов в процессе обучения функция f должна стремиться к одной из разделяющих функций. В результате обучения могут быть построены потенциальные функции для каждого образа:

, , (ф. 3)

В качестве разделяющей функции f(X) можно выбрать функцию вида:

, (ф. 4)

которая положительна для объектов одного образа и отрицательна для объектов другого.

В качестве потенциальной функции рассмотрим функцию вида

,

(ф. 5)

где _j(X) — линейно независимая система функций; _j — действительные числа, отличные от нуля для всех j = 1, 2, … ; X_i — точка, соответствующая i-му объекту из обучающей последовательности. Предполагается, что _j(X) и U(X, X_i) ограничены при XV₁  V₂; _j(X)=_j_j(X).

В процессе обучения предъявляется обучающая последовательность и на каждом n-м такте обучения строится приближение f_n(X) характеризуется следующей основной рекуррентной процедурой:

, (ф. 6)

Разновидности алгоритмов потенциальных функций отличаются выбором значений q_n и r_n, которые являются фиксированными функциями номера n. Как правило, q_n1, а r_n выбирается в виде:

, (ф. 7)

где S(f_n, f) — невозрастающие функции, причем

(ф. 8)

Коэффициенты _n представляют собой неотрицательную числовую последовательность, зависящую только от номера n. Кроме того, и (например, _n=1/n) или _n=const.

Разработано несколько вариантов алгоритмов потенциальных функций, различие между которыми состоит в выборе законов коррекции разделяющей функции от шага к шагу, т. е. в выборе законов коррекции разделяющей функции от шага к шагу, т. е. в выборе коэффициентов r_n. Приведем два основных алгоритма потенциальных функций.

1. Будем считать, что f₀(X)0 (нулевое приближение). Пусть в результате применения алгоритма после n-го шага построена разделяющая функция f_n(X), а на (n+1)-м шаге предъявлено изображение X_n+1, для которого известно действительное значение разделяющей функции f(X_n+1). Тогда функция f_n+1(X) строится по следующему правилу:

(ф. 9)

2. Во втором алгоритме также принимается, что f₀(X)0. Переход к следующему приближению, т. е. переход от функции f_n(X) к f_n+1(X), осуществляется в результате следующей рекуррентной процедуры:

(ф. 10)

где  — произвольная положительная константа, удовлетворяющая условию =(1/2)max(X, X_i).

Если в (ф. 5) принять

,

и предположить, что x_v может иметь только два значения 0 и 1, то в этом случае алгоритм потенциальных функций будет совпадать со схемой перцептрона с индивидуальными порогами А-элементов и с коррекцией ошибок. Поэтому многие теоретические положения метода потенциальных функций могут быть успешно применены для анализа некоторых перцептронных схем.