Файл: Лекция 4. Неодинаковое число испытаний на различных уровнях.doc

Скачать файл (0,55Мб)

Заказать решение

ВУЗ: Смоленский областной казачий институт промышленных технологий и бизнеса

Категория: Лекция

Дисциплина: Методы обработки экспериментальных данных

Добавлен: 29.10.2018

Просмотров: 365

Скачиваний: 11

ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.

Неодинаковое число испытаний на различных уровнях

Выше число испытаний на различных уровнях предполагалось одинаковым. Пусть число испытаний на различных уровнях, вообще говоря, различно, а именно: произведено испытаний на уровне , испытаний – на уровне испытаний – на уровне . В этом случае общую сумму квадратов отклонений находят по формуле

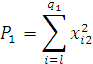
где – сумма квадратов наблюдавшихся значений признака

на уровне

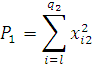
– сумма квадратов наблюдавшихся значений признака

на уровне

…

…………………………………………………………………………………….

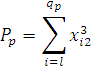
– сумма квадратов наблюдавшихся значений признака

на уровне

начений признака соответственно на уровнях

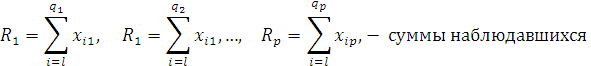
– общее число испытаний (объем выборки).

Если для упрощения вычислений из каждого наблюдавшегося значения вычитали одно и то же число C и приняли то

значений признака соответственно на уровнях ;

общее число испытаний (объем выборки.)

Если для упрощения вычислений из каждого наблюдавшегося значения вычитали одно и то же число С и приняли то

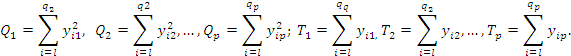
где

Факторную сумму квадратов отклонений находят по формуле

если значения признака были уменьшены то

Остальные вычисления производят, как и в случае одинакового числа испытаний:

Пример. Произведено 10 испытаний, из них 4 на первом уровне фактора, 4 – на втором и 2 – на третьем. Результаты испытаний приведены в таблице 5. Методом дисперсионного анализа при уровне значимости 0,01 проверить нулевую гипотезу о равенстве групповых средних. Предполагается, что выборки извлечены из нормальных совокупностей с одинаковыми дисперсиями.

Таблица 5

Номер испытания	Уровни фактора
i
1 2 3 4	40 44 48 36	62 80 71 91	92 76
	42	76	84

Решение. Для упрощения расчета вычтем из каждого наблюдаемого значения: . Составим расчетную таблицу 6.

Используя таблицу 6, найдем общую и факторную суммы квадратов отклонений:

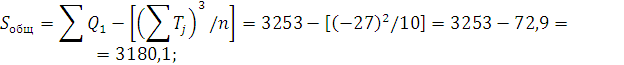
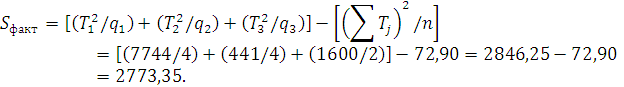
Найдем остаточную сумму квадратов отклонений:

Найдем факторную и остаточную дисперсии:

Сравним факторную и остаточную дисперсии по критерию для чего найдем наблюдаемое значение критерия:

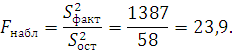
Таблица 6

Номер испытания	Уровни фактора						Итоговый столбец
i
i
1 2 3 4	-24 -20 -16 -28	576 400 256 784	-2 16	4 256 49	28 12	784 144
		2016		309		928
	-88		21		40
	7744		441		1600