Вычисленные коэффициенты напряженности позволяют дополнительно классифицировать работы по зонам. В зависимости от величины К_Н (i, j) выделяют три зоны:

• критическую - К_Н (i, j) > 0.8;

• подкритическую - 0.6 £ К_Н (i, j) £ 0.8;

• резервную - К_Н (i,j)< 0.6.

Оптимизация сетевого графика представляет собой процесс улучшения организации выполнения комплекса работ с учетом срока его выполнения. Оптимизация проводится с целью сокращения длины критического пути, выравнивания коэффициентов напряженности работ, рационального использования ресурсов.

В первую очередь принимаются меры по сокращению продолжительности работ, находящихся на критическом пути.

Это достигается:

• перераспределением всех видов ресурсов, как временных (использование резервов времени некритических путей), так и трудовых, материальных, энергетических (например, перевод части исполнителей, оборудования с некритических путей на работы критического пути); при этом перераспределение ресурсов должно идти, как правило, из зон, менее напряженных, в зоны, объединяющие наиболее напряженные работы;

• сокращением трудоемкости критических работ за счет передачи части работ на другие пути, имеющие резервы времени;

• параллельным выполнением работ критического пути;

• пересмотром топологии сети, изменением состава работ и структуры сети.

В процессе сокращения продолжительности работ критический путь может изменяться, и в дальнейшем процесс оптимизации будет направлен на сокращение продолжительности работ нового критического пути и будет продолжаться до получения удовлетворительного результата. В идеале длина любого из полных путей может стать равной длине критического пути или, по крайней мере, пути критической зоны. Тогда все работы будут вестись с равным напряжением, а срок завершения проекта существенно сократится.

На практике при попытках эффективного улучшения составленного плана неизбежно введение дополнительно к оценкам сроков фактора стоимости работ.

Оптимизация сетевого графика методом "время - стоимость" – является наиболее эффективным методом улучшения организации выполнения комплекса работ с учетом сроков их выполнения и затраченных ресурсов.

При использовании метода "время - стоимость" предполагают, что уменьшение продолжительности работы пропорционально возрастанию ее стоимости. То есть, если все запланированные работы будут выполняться с рассчитанной в сетевом графике точностью, то общая стоимость разработанного проекта будет минимальна. С ускорением работ затраты возрастают, а с их замедлением – снижаются.

Каждая работа (i, j) характеризуется продолжительностью t(i, j), которая может находиться в пределах:

,

где a(i, j) – минимально возможная (экстренная) продолжительность работы (i, j), которую только можно осуществить в условиях разработки;

---

b(i, j) – нормальная продолжительность выполнения работы (i, j).

При это стоимость с(i, j) работы (i, j) заключенная в границах от с_min(i, j) (при нормальной продолжительности работы) до с_max(i, j) (при экстренной продолжительности работы).

Используя аппроксимацию по прямой можно легко найти изменение стоимости работы Dс(i, j) при сокращении ее продолжительности на величину:

.

Величина h(i, j), равная тангенсу угла a наклона аппроксимирующей прямой показывает затраты на ускорение работы (i, j) (по сравнению с нормальной продолжительностью) на единицу времени:

.

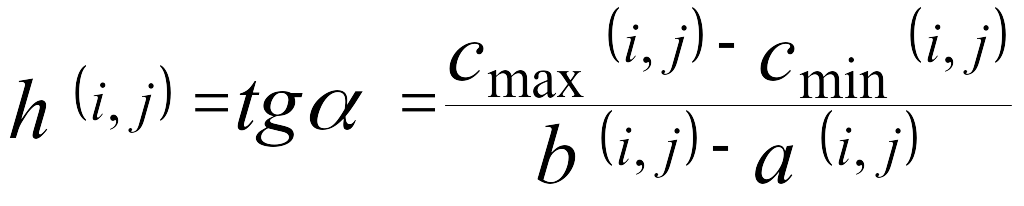Самый очевидный вариант частной оптимизации сетевого графика с учетом стоимости предполагает использование резервов времени работ. Продолжительность каждой работы, имеющей резерв времени, увеличивают до тех пор, пока не будет исчерпан этот резерв или пока не будет достигнуто верхнее значение продолжительности b(i, j). При этом стоимость выполнения проекта, равная до оптимизации:

,

уменьшится на величину:

.

Для проведения частной оптимизации сетевого графика кроме продолжительности работ t(i, j), необходимо знать их граничные значения а(i, j) и b(i, j), а также показатели затрат на ускорение работ h(i, j), вычисляемые по вышеуказанной формуле. Продолжительность каждой работы t(i, j) целесообразно увеличить на величину такого резерва, чтобы не изменить ранние (ожидаемые) сроки наступления всех событий, т.е. на величину свободного резерва времени R_C(i, j).

В реальных условиях выполнения проекта может потребоваться ускорение его выполнения, что, естественно, отразится на стоимости проекта: она увеличится. Поэтому необходимо определить оптимальное соотношение между стоимостью проекта С и продолжительностью его выполнения t = t_КР, представленное, например, в виде функции С = С(t).

Для оптимизации сетей и, в частности, для нахождения функции С(t) могут быть использованы эвристические методы, т.е. методы, учитывающие индивидуальные особенности сетевых графиков.

В практике сетевого планирования при необходимости можно также осуществить комплексный анализ ресурсной, экономической и финансовой реализуемости разработанных планов.

Анализ ресурсной реализуемости выполняется в два этапа. На первом – устанавливается наличие ресурсов по всем работам, а на втором – разрабатываются способы их рационального использования. Экономическая и финансовая реализуемость сетевых моделей тесно связаны между собой. Анализ экономической реализуемости проектных работ необходим для обоснования продолжительности их осуществления, при которой может быть достигнут наибольший финансовый результат.

Таким образом, сетевое планирование, при правильном его использовании, может позволить предприятию наиболее конструктивно строить свою деятельность в условиях рынка. Что, в конечном счете, позволяет предприятию не только функционировать, наиболее эффективно используя имеющиеся ресурсы, но и успешно развиваться.

---

Постановка задачи. Описание модели

Предприятие планирует выпустить новый вид продукции. Для реализации этого проекта составлен перечень необходимых работ, отраженный в следующей таблице.

Операция	Описание работы	Начальное событие	Конечное событие	Наиболее вероятная продолжительность
A	Обоснование цели проекта	0	1	2
B	Проведение маркетинговых исследований	1	2	5
C	Разработка технических условий	1	3	3
D	Эскизное проектирование	1	4	4
E	Выбор поставщиков ресурсов	2	5	2
F	Фиктивная работа	3	9	0
G	Техническое проектирование	4	6	5
H	Расчет потребности ресурсов	5	8	2
I	Рабочее проектирование	6	7	10
J	Закупка производственных ресурсов	8	9	10
K	Изготовление деталей	7	9	8
L	Сертификация деталей	8	11	2
M	Согласование сроков поставки	7	11	3
N	Разработка технологии сборки	9	10	3
O	Сборка изделия	10	11	11
P	Отправка продукции потребителю	11	12	5

Оптимистическое время завершения проектных работ на единицу меньше заданного, а пессимистическое – на единицу больше.

Необходимо:

построить сетевой график.

Найти итоговое решение (критический путь) при помощи системы PERT.

Проанализировать полученные результаты.

Сетевой график выполнения проекта

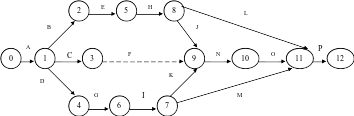
Анализ полученных результатов

Ожидаемое время завершения проекта – 48 недель.

В результате расчетов мы получили критический путь, проходящий через события 0, 1, 4, 6, 7, 9, 10, 11.

Рассмотрим прежде всего оптимизацию сетевого графика по критерию минимизации затрат времени на выполнение отдельных процессов и всего проекта. Общий срок свершения всех работ в сетевой модели следует сокращать в первую очередь за счет уменьшения критического пути.

Анализируя резервы времени, можно сделать вывод о том, что с целью сокращения критического пути необходимо уменьшать продолжительности работ A, D, G, I, K, N, O, P. То есть, разработчикам проекта или руководителям рассматриваемой фирмы следует обратить внимание и по возможности, с целью уменьшения затрат проекта в целом, уменьшить продолжительность следующих работ:

• обоснование цели проекта;

• эскизное проектирование;

• техническое проектирование;

• рабочее проектирование;

• изготовление деталей;

• разработка технологии сборки;

• сборка изделия;

• отправка продукции потребителю.

Кроме того, следует провести анализ данной модели с целью выравнивания продолжительности наиболее напряженных путей.

В разработанном сетевом графике можно выделить пять полных путей. Их коэффициента напряженности будут соответственно равны:

---

1. Первый путь проходит через события 0-1-2-5-8-11-12 и равен 18 неделям. Коэффициент напряженности этого пути составляет:

К_Н = 18/48 = 0,375

2. Второй путь проходит через события 0-1-2-5-8-9-10-11-12 и равен 40 неделям. Коэффициент напряженности этого пути составляет:

К_Н = 40/48 = 0,833

3. Третий путь проходит через события 0-1-3-9-10-11-12 и равен 24 неделям. Коэффициент его напряженности составляет:

К_Н = 24/48 = 0,5

4. Четвертый путь – это критический путь, коэффициент напряженности которого равен 1,0.

5. Пятый путь проходит через события 0-1-4-6-7-11-12. Его продолжительность составляет 29 дней, а коэффициент напряженности:

К_Н = 29/48 = 0,604

Анализ коэффициентов напряженности путей подтверждает возможность сокращения критического пути почти в три раза при более рациональной загрузке имеющихся трудовых ресурсов.

Из расчетов следует, что наименее напряженными оказались пути выполнения плановых работ, а наиболее напряженными – проектно-конструкторских. Это значит, что при необходимости сокращения критического пути, следует дополнительно привлечь к работе конструктора.

Если рассматривать оптимизацию данной модели за счет минимизации расходования материальных ресурсов, то одним из возможных способов сокращения критического пути может служить перераспределение различных ресурсов с ненапряженных путей на выполнение критических работ.

---

Смотрите также файлы

• Пример инновационного проекта.docx

• Отбор и оценка проектов.pdf

• Организационные структуры проектно ориентированных организаций.docx

• Методические рекомендации по оценке эфективности инвестиционных проектов.doc

• Американ. стандарт 4-е издание.pdf