Добавлен: 29.10.2018
Просмотров: 303
Скачиваний: 11
Г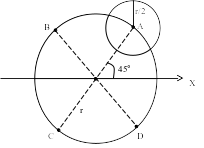
рафика
и рекурсивные алгоритмы
Рассмотрим пример рисования рекурсивной самоподобной фигуры.
Основная фигура – окружность радиуса r с четырьмя меньшими окружностями радиусов r/2 с центрами в точках A, B, C, D. Точка А расположена на основной окружности под углом 45 градусов от горизонтали, точка B – под углом 135°=90°+45° от горизонтали,
точка С – под углом 225°=180°+45° от горизонтали, точка D – под углом 315°=45°+ 90°+90°+90°. Если координаты центра основной окружности Xc, Yc, тогда точки A, B, C, D будут иметь координаты:
A (Xc+ r cos45°, Yc+ r sin45°)
B (Xc+ r cos(45°+90°), Yc+ r sin(45°+90°))
C (Xc+ r cos(45°+2 90°), Yc+ r sin(45°+2 90°))
D (Xc+ r cos(45°+3 90°), Yc+ r sin(45°+3 90°))
Далее, для каждой малой окружности повторяем процедуру отрисовывания вспомогательных меньших окружностей. Процесс останавливается, когда текущий радиус меньших окружностей становится меньше заданной величины.
Алгоритм рисования самоподобной фигуры
Круги(300, 300, 200, 10)
Функция круги(xc, yc, r, rmin)
Если r<rmin тогда
Выход
КонецЕсли
Круг (r, xc, yc)
P=pi()/4
Цикл по i от 0 до 3
xc1=xc+r*cos(p+i*p*2)
yc1=yc+r*sin(p+i*p*2)
круги(xc1, yc1, r/2, rmin)
КонецЦикла
В результате выполнения этой процедуры должна получиться фигура:
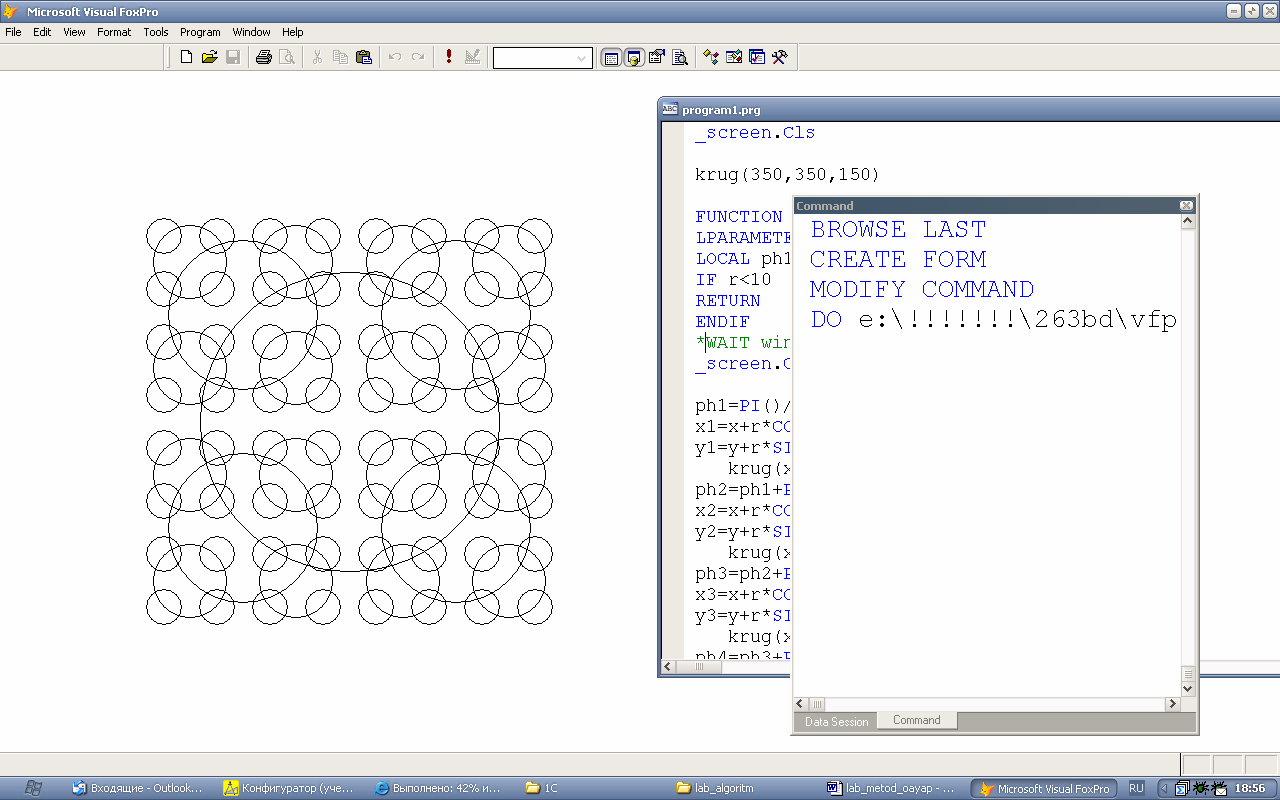
1.
_screen.Cls
krug(350,350,150)
FUNCTION krug
LPARAMETERS x,y,r
LOCAL ph1,ph2,ph3,ph4
IF r<10
RETURN
ENDIF
WAIT window "hhh"
_screen.Circle(r,x,y)
ph1=PI()/4
x1=x+r*COS(ph1)
y1=y+r*SIN(ph1)
krug(x1,y1,r/2)
ph2=ph1+PI()/2
x2=x+r*COS(ph2)
y2=y+r*SIN(ph2)
krug(x2,y2,r/2)
ph3=ph2+PI()/2
x3=x+r*COS(ph3)
y3=y+r*SIN(ph3)
krug(x3,y3,r/2)
ph4=ph3+PI()/2
x4=x+r*COS(ph4)
y4=y+r*SIN(ph4)
krug(x4,y4,r/2)
RETURN

2.
_screen.Cls
krug(350,350,150)
FUNCTION krug
LPARAMETERS x,y,r
LOCAL ph1,ph2,ph3,ph4
IF r<10
RETURN
ENDIF
*WAIT window "hhh"
_screen.Circle(r,x,y)
ph1=PI()/3
x1=x+r*COS(ph1)
y1=y+r*SIN(ph1)
krug(x1,y1,r/2)
ph2=ph1+PI()*2/3
x2=x+r*COS(ph2)
y2=y+r*SIN(ph2)
krug(x2,y2,r/2)
ph3=ph2+PI()*2/3
x3=x+r*COS(ph3)
y3=y+r*SIN(ph3)
krug(x3,y3,r/2)
RETURN