Файл: СЕТИ СВЯЗИ.doc

Скачать файл (2,02Мб)

Заказать решение

ВУЗ: Не указан

Категория: Методичка

Дисциплина: Сети связи

Добавлен: 19.10.2018

Просмотров: 1125

Скачиваний: 12

ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.

Нормативное значение потерь в обходном направлении Робх. н, известно и равно 0,01.

Отсюда можно определить Рэкв по формуле:

= . (8)

Рассматривая ( S + Vобх ) как общий полнодоступный пучок, можно применить для его расчета формулу Эрланга:

= * () . (9)

Из (9) методом подбора или используя [161, [14, с- 28-33], можно найти величину (Vобх + S ). Зная число каналов в эквивалентном пучке, нетрудно найти Vобх.

К задачам 3, 4

Материал к задачам 3 и 4, посвященный изучению метода рельефов динамического управления потоками вызовов, изложен в основной литературе [2, с.121-126] и дополнительной [6, с. 172-174; 9; 4, с. 56-59]. Схемы децентрализованной и централизованной систем управления потоками можно найти в [4, с. 35-39].

По заданию требуется построить рельеф только для одного i-го УК. Построенным i -рельефом можно пользоваться только при установлении соединения от любого другого УКj к узлу i.

Фиксируется соседний с УКi. узел j. Стрелка, исходящая от узла j к узлу i и показывающая вес этого направления, должна иметь высоту 1 , что имеет тот физический смысл, что при установлении соединения от УКj до УКi используется путь в один транзитный участок. Если рассмотреть расстояние от узлов, соседних узлу j , то, очевидно, путь установления соединения от этих узлов по направлению к узлу j будет иметь длину на один транзитный блок больше, т.е. 2, и т.д. Присвоение рельефа на графе сети можно проводить, пользуясь следующим простым алгоритмом.

1. Рассмотрим произвольный УКr. Управляющее устройство рассматривает веса исходящих стрелок и выбирает стрелку с минимальной высотой. Эта высота считается высотой узла : = {}, где -высота ребра . Физический смысл этого действия заключается в том, что на узле отмечается кратчайший путь в числе транзитных участков.

2. Высота , рассылается соседям. ЭУМ соседнего узла , приняв отмечает направление, ведущее от к r, высотой ( + 1 ), придерживаясь того правила, что если путь от соседнего УКr, дo УКi составляет некоторое число транзитных участков, то от УКω этот путь будет на 1 участок длиннее.

Придерживаясь такого алгоритма, можно сформировать рельеф всей сети, при этом алгоритм является децентрализованным, каждая ЭУМ работает независимо от ЭУМ других УК. Однако между узлами передается информация об их весах. Пример рельефа для УК показан для графа сети на рис. 4. Для практического использования на сетях связи алгоритм несколько видоизменен. Когда ЭУМ УК ведет просмотр направлений с целью вычисления своей высоты, она учитывает, для какого узла вычисляется высота, и исключает из рассмотрения направление, ведущее к этому узлу. Это позволяет избежать образования петель. Например, если Н3 посылается к УК2,то из рассмотрения исключается высота h₃₂ и в результате Н =3. Новый вес ребра b₂₃ приведен в кружочке. Это позволяет исключить из рассмотрения путь .

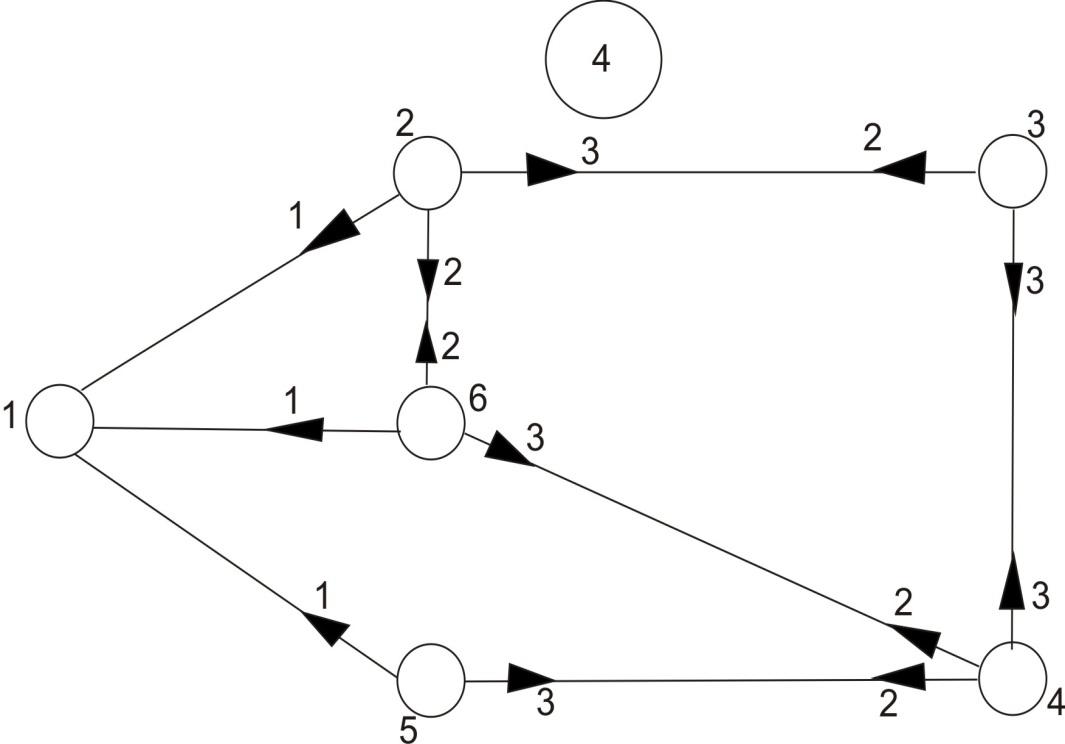
Рис. 5.

Алгоритм метода рельефа обладает свойством исправлять неправильные веса, которые могут возникнуть в том случае, если в сети вышло из строя ребро или им нельзя пользоваться в результате возникшей перегрузки. Управляющее свойство узла, на котором это произошло, сообщает всем своим соседям новый вес, если, конечно, вышло из строя направление с минимальным весом.

Таким образом, рельеф соседних узлов меняется в соответствии с заданным выше алгоритмом. Если высота УК в результате выхода из строя ребра не меняется, изменения рельефа на соседних УК не происходит.

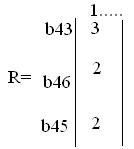
В задании требуется составить матрицу маршрутов для УКj. Лучше всего привести матрицу рельефов и на ней пояснить построение матрицы маршрутов. Пусть матрицу маршрутов требуется построить для УК4 сети, (рис.5). Ниже приведены соответствующие столбцы матрицы рельефа R4 и маршрутов М4 . Веса в матрице рельефов обозначают число транзитных участков в кратчайшем пути от УК4 до УК1, если устанавливать соединение по направлению .

Числа в матрице маршрутов задают порядок выбора направлений [4, с. 35-39].

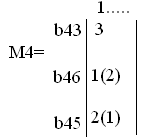
Заметим, что направление и с точки зрения выбранного критерия равноценны, поэтому в скобках в М₄ указан другой возможный вариант порядка выбора.

Если вышло из строя какое-либо ребро сети, то необходимо провести изменение рельефа (лучше всего это сделать на новом чертеже графа сети), затем сформировать для этого случая заданный столбец матриц рельефа и маршрута.

К задаче 5

Материал к задаче 5, посвященной изучению метода распределения потоков нагрузки на ГТС при проектировании новой станции, изложен в литературе [17] . В соответствии с методом Раппа предполагается, что включение на сети новой АТС не окажет влияния на общий исходящий поток нагрузки существующих АТС. Нагрузка на новую станцию создается за счет пропорционального снижения нагрузки с существующих направлений и передачи ее на направление к новой АТС.

Пусть матрица потоков нагрузки до включения новой АТС размерностью n*n имеет вид:

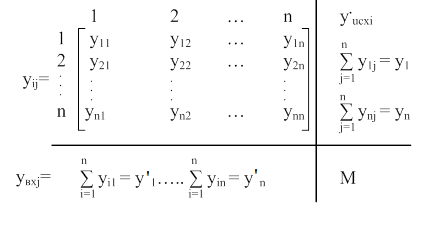(10)

В выражении (10) исходящие и входящие потоки нагрузки на АТС определяются суммированием соответствующих строк и столбцов матрицы, общая нагрузка на сети равна сумме элементов матрицы (10):

Допустим, что новая (n+1) АТС имеет исходящую нагрузку равную входящей, а внутристанционную - . Для организации столбца (n+1) входящей нагрузки на необходимо снять с существующих направлений нагрузку -.

Рассчитаем коэффициент снятия нагрузки

X= (11)

который показывает, какую часть нагрузки необходимо снять с каждого Эрланга существующих направлений и передать на новую АТС. Тогда столбец (n+1) для новой АТС запишется следующим образом:

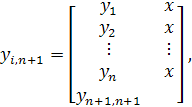(12)