Добавлен: 19.10.2018
Просмотров: 4022
Скачиваний: 59
СОДЕРЖАНИЕ
1.Исследование функции на безусловный экстремум
2. Численные методы безусловной минимизации
Метод конфигураций (Хука-Дживса)
Метод деформируемого многогранника (Нелдера-Мида)
Метод наискорейшего градиентного спуска
Метод сопряженных направлений (Флетчера – Ривса)
Порядок выполнения лабораторной работы
Пример выполнения лабораторной работы
3. Решение задачи минимизации со смешанными ограничениями
Седловые точки функции Лагранжа
Метод седловой точки в задачах квадратичного программирования
Метод проекции градиента для задачи условной оптимизации
Метод условного градиента для задачи условной оптимизации
Метод возможных направлений для задачи условной оптимизации
Порядок выполнения лабораторной работы
Пример выполнения лабораторной работы
4. Основные понятия линейного программирования
Модель задачи линейного программирования
Свойства задачи линейного программирования
Двойственность в линейном программировании
Построение модели транспортной задачи
Методы нахождения начального плана перевозок.
Задание 2. Числовые характеристики симметричной квадратной матрицы.
Задание 3. Формула Тейлора для функции нескольких переменных
Задание 4. Нахождение локальных экстремумов
Задание 5. Одномерная оптимизация
Задание 6. Многомерная оптимизация по направлению
Задание 7. Методы безусловной оптимизации
Задание 8. Методы условной оптимизации
Задание 9. Задача линейного программирования и симплекс-метод
Задание 10. Транспортная задача
МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ
ТУ-УГМК
С.П Трофимов
Контрольная работа
Методическая разработка для заочной формы обучения
по
дисциплине
«Методы оптимизации»
В.Пышма
Оглавление
1.Исследование функции на безусловный экстремум 3
2. Численные методы безусловной минимизации 5
Метод конфигураций (Хука-Дживса) 7
Метод деформируемого многогранника (Нелдера-Мида) 7
Метод наискорейшего градиентного спуска 8
Метод сопряженных направлений (Флетчера – Ривса) 9
Порядок выполнения лабораторной работы 10
Пример выполнения лабораторной работы 10
3. Решение задачи минимизации со смешанными ограничениями 17
Седловые точки функции Лагранжа 20
Метод седловой точки в задачах квадратичного программирования 21
Метод проекции градиента для задачи условной оптимизации 23
Метод условного градиента для задачи условной оптимизации 23
Метод возможных направлений для задачи условной оптимизации 23
Порядок выполнения лабораторной работы 24
Пример выполнения лабораторной работы 24
4. Основные понятия линейного программирования 36
Модель задачи линейного программирования 36
Свойства задачи линейного программирования 38
Двойственность в линейном программировании 38
5. Задача транспортного типа 40
Построение модели транспортной задачи 40
Методы нахождения начального плана перевозок. 44
Задание 2. Числовые характеристики симметричной квадратной матрицы. 48
Задание 3. Формула Тейлора для функции нескольких переменных 49
Задание 4. Нахождение локальных экстремумов 49
Задание 5. Одномерная оптимизация 49
Задание 6. Многомерная оптимизация по направлению 49
Задание 7. Методы безусловной оптимизации 49
Задание 8. Методы условной оптимизации 52
Задание 9. Задача линейного программирования и симплекс-метод 53
Задание 10. Транспортная задача 57
Теоретическая часть
1.Исследование функции на безусловный экстремум
Рассматривается задача
 f(x)→
extr,
x
f(x)→
extr,
x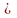 En. (1)
En. (1)
Метод поиска безусловного экстремума основывается на следующих условиях оптимальности:
-
Необходимое условие оптимальности 1- порядка
Пусть
функция f(x)
дифференцируема в точке х*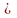 Еn.
Тогда если х*
локальное решение задачи (1), то
Еn.
Тогда если х*
локальное решение задачи (1), то
grad f(x*)=0 (2)
-
Необходимое условие оптимальности 2- порядка
Пусть
функция f(x)
дважды дифференцируема в точке х*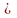 Еn.
Тогда
Еn.
Тогда
-
Если х* - точка локального минимума в задаче (1), то матрица Гессе Н(х*) неотрицательно определена, то есть,
 р
р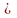 Еn
выполняется неравенство (Н(х*)
р,р) ≥0.
Еn
выполняется неравенство (Н(х*)
р,р) ≥0. -
Если х* - точка локального максимума в задаче (1), то матрица Н(х*) неположительно определена, то есть,
 р
р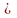 Еn
выполняется (Н(х*)
р,р)
≤0.
Еn
выполняется (Н(х*)
р,р)
≤0. -
Достаточное условие оптимальности 2- порядка
Пусть
функция f(x)
дважды дифференцируема в точке х*
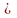 Еn
и grad
f(x*)=0.
Еn
и grad
f(x*)=0.
-
Если матрица Н(х*) положительно определена, то есть, (Н(х*) р,р) > 0,
 p
p
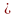 Еn,
р≠0, то х*
- точка строгого локального минимума
функции f(x)
на Еn.
Еn,
р≠0, то х*
- точка строгого локального минимума
функции f(x)
на Еn. -
Если матрица Н(х*) отрицательно определена, то есть, (Н(х*) р,р) <0
 p
p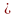 Еn,
р≠
0, то х*
- точка строгого локального максимума
функции f(x)
на Еn.
Еn,
р≠
0, то х*
- точка строгого локального максимума
функции f(x)
на Еn. -
Если матрица Н(х*)-знакопеременная, то х* не является точкой локального экстремума.
-
Если матрица Н(х*)- полуопределеная, то об оптимальных свойствах х* ничего сказать нельзя, нужны дополнительные исследования.
Если grad f(x*)=0, то х* называется стационарной точкой. Для выпуклой (вогнутой) на Еn функции стационарные точки являются точками ее глобального минимума (максимума). Строго выпуклые (вогнутые) функции имеют единственный глобальный минимум (максимум).
Критерий
выпуклости функции.
Дважды непрерывно дифференцируемая на
выпуклом множестве Х
с непустой внутренностью функция
является выпуклой (вогнутой) на этом
множестве в том и только том случае,
когда матрица Гессе Н(х*)
неотрицательно (неположительно)
определена для всех х
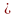 Х.
Х.
При исследовании на знакоопределенность матрицы вторых производных функции рекомендуется применять критерий Сильвестра или анализ собственных значений матрицы.
Схема поиска безусловных экстремумов функции:
-
Составить и решить систему алгебраических уравнений (2).
-
В стационарных точках x* (точках, являющихся решением системы (2)) исследовать на знакоопределенность матрицу вторых производных. Точки, в которых гессиан Н(x*) положительно определен, являются точками глобального минимума; стационарные точки, в которых Н(х*) отрицательно определен, являются точками глобального максимума. Если гессиан знакопеременный, то x* не является экстремумом. Если гессиан полуопределенный, то для определения оптимальности нужны дополнительные исследования.
-
Исходя из вида исследуемой функции, проанализировать стационарные точки, в которых матрица вторых производных не является строго знакоопределенной.
-
Найденные точки локального экстремума исследуются на глобальный экстремум (если это возможно). В частность, если матрица Гессе неотрицательно (неположительно) определена на всем пространстве Еn, то все стационарные точки функции являются точками глобального минимума (максимума).
2. Численные методы безусловной минимизации
Численное решение задачи минимизации (1), как правило, связано с построением минимизирующей последовательности точек x0,x1,x2,…,xn,…, обладающих свойством
f(xk)<f(xk-1), k=0,1,… (3)
Общее правило построения минимизирующей последовательности имеет вид
xk+1=xk+tkdk, k=0,1,....,
где х0 начальная точка поиска, dk приемлемое направление перехода из точки xk
в точку xk+1, которое обеспечивает выполнение условий (3) и называется направлением спуска, tk величина шага. Начальная точка поиска задается, исходя из физического содержания решаемой задачи и априорных данных о наличии и положении точек экстремума.
При решении вопроса о выборе численного метода рекомендуется оценить поведение линий уровня целевой функции в окрестностях предполагаемой точки экстремума. Число m = L/l, где L - максимальное, а l-минимальное собственные значения гессиана функции f в предполагаемой точке экстремума x0 (характеризующее, вообще говоря, разброс собственных значений оператора f (x)) называют числом обусловленности гессиана функции f в точке x0. Если m >> 1, то функцию называют плохо обусловленной или овражной. “Овражность”, то есть вытянутость линий уровня вдоль одного направления, приводит к тому, что градиентные методы сходятся медленно.
В зависимости от наивысшего порядка частных производных функции f(x), используемых для формирования dk и tk, численные методы принято делить на три группы:
-
Методы нулевого порядка, использующие информацию только о значениях функции f(x) (методы деформируемого многогранника, конфигураций). Эти методы могут применяться в тех случаях, когда функция задана неявно или не задана аналитически, но известен ряд значений функции или эти значения вычисляются непосредственно в ходе реализации алгоритма. Они также могут быть полезны в случаях, когда производные функции могут быть заданы аналитически, но их выражения очень громоздки.
-
Методы первого порядка, использующие информацию о значениях самой функции f(x) и ее первых производных (методы наискорейшего градиентного спуска, дробления шага, Гаусса-Зейделя, Флетчера-Ривса).
-
Методы второго порядка, использующие, кроме того, и информацию о вторых производных функции f(x) (метод Ньютона и его модификации)
Метод конфигураций (Хука-Дживса)
Состоит из двух этапов: 1) исследование с циклическим изменением переменных и 2) ускорение поиска по образцам.
Исследующий поиск начинается в точке х0, называемой старым базисом. Направления поиска – координатные направления. По каждому направлению поочередно с шагом +t0 (-t0), проверяется выполнение условия (2), и в качестве нового базиса берется точка, с координатами, полученными в результате удачных шагов из начальной точки по каждому направлению.
Направление от старого базиса к новому задает направление ускорения поиска: в качестве следующей точки минимизирующей последовательности проверяется точка y1=x0+(x1-x0). Здесь - ускоряющий множитель, задаваемый пользователем. Если полученная точка является удачной, то она берется в качестве следующей точки для исследования. В противном случае исследование ведется из точки x1.
Метод деформируемого многогранника (Нелдера-Мида)
Строится последовательность множеств из n+1 точек, которые являются вершинами выпуклого многогранника. На каждом последующем k+1-м шаге из системы точек xi(k), i=1, … ,n+1, выводится точка xh(k), в которой функция f(x) имеет наибольшее значение (худшая точка). Вместо точки xh(k) в систему вводится новая точка, выбираемая на отрезке прямой, проходящей через худшую точку и центр тяжести оставшихся n вершин многогранника:
xn+2=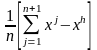 - центр тяжести;
- центр тяжести;
xn+3= xn+2+( xn+2- xh) – новая точка (“растянутое” отражение наихудшей вершины).
Метод дробления шага
Строится последовательность точек {xk}, k=0,1,..., таких, что f(xk)<f(xk-1), k=0,1,... .Точки последовательности{xk} вычисляются по правилу
xk+1=xk-tkgrad f(xk), k=0,1,.... (4)
Точка х0 задается пользователем; grad f(xk) – градиент минимизируемой функции, вычисленный в точке xk; величина шага t0 задается пользователем и остается постоянной до тех пор, пока функция убывает в точках последовательности, что контролируется путем проверки выполнения условия
f(xk+1)-f(xk) <0 (или <-ε). Если условие убывания не выполняется, величина шага уменьшается, как правило, вдвое, то есть, tk=tk/2.
Метод наискорейшего градиентного спуска
Строится последовательность точек {xk}, k=0,1,..., таких, что f(xk)<f(xk-1), k=0,1,... .Точки последовательности {xk} вычисляются по правилу
xk+1=xk-tkgrad
f(xk),
k=0,1,...
. Точка х0
задается пользователем; grad
f(xk)
– градиент минимизируемой функции,
вычисленный в точке xk;
величина шага tk
определяется из условия минимума функции
φ(tk)=а(xk-tkgrad
f(xk)).
Задача минимизации одномерной функции
φ(tk)
может быть решена с использованием
необходимого условия минимума
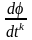 =0
с последующей проверкой достаточного
условия минимума
=0
с последующей проверкой достаточного
условия минимума
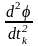 >0
или с использованием численных методов.
>0
или с использованием численных методов.
Метод сопряженных направлений (Флетчера – Ривса)
Строится последовательность точек {xk}, k=0,1,..., таких, что f(xk)<f(xk-1), k=0,1,... .Точки последовательности{xk} вычисляются по правилу:
xk+1=xk-tkdk, k=0,1,....;
dk=- grad f(xk)+βk-1dk-1; (4)
d0=- grad f(x0);
βk-1=║ grad f(xk)║2∕║ grad f(xk-1)║2
Точка
х0
задается пользователем; величина шага
tk
определяется из условия минимума функции
φ(t)=а(xk-t
dk)).
Задача минимизации одномерной функции
φ(tk)
может быть решена с использованием
необходимого условия минимума (dφ/dt)=0
с последующей проверкой достаточного
условия минимума
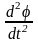 >0
или с использованием численных методов.
>0
или с использованием численных методов.
Метод Ньютона
Строится последовательность точек {xk}, k=0,1,..., таких, что f(xk)<f(xk-1), k=0,1,... .Точки последовательности{xk} вычисляются по правилу xk+1=xk+dk, k=0,1,..... Точка х0 задается пользователем с учетом знакопостоянства и невырожденности матрицы Гессе в задаваемой начальной точке и близости выбранной точки к предполагаемой точке минимума. Направление спуска определяется для каждого значения k по формуле
dk=-H-1(xk)grad f(xk), где Н – матрица Гессе.
Порядок выполнения лабораторной работы
-
Записать необходимые условия экстремума. Аналитически или используя прикладные пакеты найти стационарные точки.
-
Проверить выполнение достаточных условий экстремума в найденных стационарных точках. Найти глобальный минимум функции. Оценить обусловленность задачи в точке минимума и “овражность” графика в окрестности точки минимума. Сделать предварительный вывод о работоспособности избранного численного метода.
-
Выбрать пакет, в котором будет строиться график. Рекомендации приведены в Приложении. Построить график функции, задавая пределы изменения координат с учетом аналитически найденных точек минимума – максимума.
-
Выбрать несколько начальных точек для реализации численного метода. Задать критерий завершения итерационного процесса. Найти минимум. Сравнить результаты с аналитически найденным значением глобального минимума. Исследовать сходимость алгоритма, фиксируя точность определения минимума, количество итераций метода и количество вычислений минимизируемой функции в зависимости от задаваемой точности поиска. Результатом выполнения данного пункта должны быть выводы об объёме вычислений в зависимости от задаваемой точности и начального приближения.