Практическая работа №1

Определение параметров задания моделируемых тел

Основные определения

Трехмерное тело – область пространства, состоящая из однородного материала и ограниченная замкнутой поверхностью, состоящей из граней. Любое трехмерное тело состоит из базовых трехмерных элементов: граней, ребер и вершин.

Грань – гладкая (не обязательно плоская) часть поверхности детали, ограниченная замкнутым контуром из ребер.

Ребро – пространственная кривая произвольной конфигурации, полученная на пересечении двух граней.

Вершина – точка в трехмерном пространстве. Для твердого тела это может быть точкой на конце ребра или пересечении ребер.

Для задания трехмерных тел с плоскими гранями и прямолинейными ребрами достаточно задать координаты вершин и связи между вершинами.

Если тело имеет плоские грани и криволинейные ребра, для таких ребер должны быть заданы также либо набор функций, описывающих сегменты ребер, либо множество точек в плоскости грани, образующих данное ребро с заданным расстоянием между этими точками. Чем меньше данное расстояние, тем точнее данное множество точек описывает форму данного ребра.

Если тело содержит неплоские грани, для их задания могут быть использованы формообразующие операции на основе плоских эскизов. Данный способ лежит в основе твердотельного моделирования в системах автоматизированного проектирования.

Практическая работа №2

Задание вершин и связей трехмерных тел в программе

Основные определения

Трехмерное тело – область пространства, состоящая из однородного материала и ограниченная замкнутой поверхностью, состоящей из граней. Любое трехмерное тело состоит из базовых трехмерных элементов: граней, ребер и вершин.

Грань – гладкая (не обязательно плоская) часть поверхности детали, ограниченная замкнутым контуром из ребер.

Ребро – пространственная кривая произвольной конфигурации, полученная на пересечении двух граней.

Вершина – точка в трехмерном пространстве. Для твердого тела это может быть точкой на конце ребра или пересечении ребер.

Для задания трехмерных тел с плоскими гранями и прямолинейными ребрами достаточно задать координаты вершин и связи между вершинами.

Если тело имеет плоские грани и криволинейные ребра, для таких ребер должны быть заданы также либо набор функций, описывающих сегменты ребер, либо множество точек в плоскости грани, образующих данное ребро с заданным расстоянием между этими точками. Чем меньше данное расстояние, тем точнее данное множество точек описывает форму данного ребра.

Если тело содержит неплоские грани, для их задания могут быть использованы формообразующие операции на основе плоских эскизов. Данный способ лежит в основе твердотельного моделирования в системах автоматизированного проектирования.

---

Ввод параметров тела в программу

Для ввода параметров трехмерного тела в программу могут использоваться следующие способы:

1. Задание константных значений в тексте программы. Для этого в программе должны быть объявлены структуры данных типа массив или список, каждому элементу которых присваиваивается соответствующее значение координат и признаки наличия связей между вершинами в определенном формате.

2. Формирование файла с указанием координат вершин и связей между ними в определенном формате. Для считывания данных из этого файла программа должна реализовывать алгоритмы, позволяющие распознавать отдельные параметры в соответствие с форматом файла и записывать их во внутренние структуры данных типа массив или список (см. пункт 1).

3. Ввод данных посредством пользовательских форм или таблиц. При этом программа должна обеспечивать определенный пользовательский интерфейс, позволяющий вводить все необходимые параметры, и запись данных значений во внутренние структуры данных (см. пункт 1).

Сведения о массивах

Массив представляет собой структуру данных смежного типа. Массив - это непрерывная область памяти фиксированной длины. Все элементы массива имеют одинаковый размер и структуру и располагаются внутри области памяти массива без каких-либо пропусков.

Определение местоположения элементов массива в памяти производится по индексу элемента, который может принимать значения от 0 до N-1, где N – количество элементов массива. При этом адрес памяти заданного элемента одномерного массива вычисляется с помощью следующей формулы:

Адрес памяти элемента одномерного массива

Адрес начала области памяти массива

Размер элемента массива

Индекс элемента массива

= + *

В VBA объявление массива производится в соответствие со следующей синтаксической конструкцией:

Dim varname[([number of items])] [As type],

где:

Dim – ключевое слово, использующееся для объявления переменных и структур данных;

Varname – имя массива;

Number of items – количество элементов массива;

As – ключевое слово, использующееся для задания типа;

Type – тип элементов массива.

Например:

Dim DayArray(50) as Boolean - объявление одномерного массива DayArray из 50-ти элементов логического типа;

Dim Matrix(3, 4) As Integer - объявление двухмерного массива Matrix, представляющего собой таблицу элементов целого типа с 3-мя строками и 4-мя столбцами.

Для записи значений в элементы массива используется операция присваивания в соответствие со следующим с синтаксисом:

Name (Index,[Index, …]) = value,

где:

Name – имя массива;

Index – номер элемента массива;

Value – присваиваемое значение.

Например:

Matrix(0,3) = 5 - присваивание значения 5 элементу двухмерного массива, находящемуся на пересечении 1- строки и 4-го столбца (от нуля);

Links(3) = 10 - присваивание значения 10 4-му элементу (от нуля) одномерного массива Links.

---

Практическая работа №3

Отображение трехмерных тел

Отображение трехмерного тела на экране компьютера производится с помощью программы, в которой используются графические функции программного интерфейса языка программирования или операционной системы.

Для отображения простейших тел с плоскими гранями и прямолинейными ребрами необходимы исходные данные в виде координат вершин и связей между вершинами, которые определяют множество ребер тела.

Так как экран представляет собой плоскость, то прежде чем производить отображение трехмерного тела, необходимо задать проекцию данного тела на плоскость экрана. Первоначальная проекция представляет собой вид тела под углом зрения, образующим перпендикуляр к плоскости экрана. Он совпадает по направлению с осью Z. Две других координатных оси задают плоскость экрана. Ось X определяет положение точек (пикселей) изображения по горизонтали, а ось Y- по вертикали. Центр координат находится в верхнем левом углу экрана. Ось X направлена вправо, ось Y – вниз.

Ребра текущей проекции заданного трехмерного тела представляют собой отрезки, соединяющие вершины тела. Данные отрезки выводятся на экран с помощью графической функции F_Line, требующей задания следующих входных параметров:

1. значение координаты X в пикселях первого конца отрезка;

2. значение координаты Y в пикселях первого конца отрезка;

3. значение координаты X в пикселях второго конца отрезка;

4. значение координаты Y в пикселях второго конца отрезка;

5. цвет отрезка в виде числового кода, получаемого функцией RGB на основе кодов интенсивности красного, зеленого и синего цветов;

6. толщина линии отрезка в пикселях.

Вызов функции производится только для тех пар вершин, между которыми задана связь.

Например:

For i = 0 To LinkedNodes - 1

If lm(fp(i), sp(i)) Then

F_Line nx1(fp(i)), ny1(fp(i)), nx1(sp(i)), ny1(sp(i)), ItemsCol, 2

End If

Next,

где:

LinkedNodes – переменная, содержащая количество связей между вершинами;

fp, sp - массивы, содержащие номера вершин каждой связи i;

lm - двухмерный массив, представляющий собой таблицу, строки которой соответствуют номерам начальных вершин, а столбцы – номерам конечных вершин; на пересечении строк и столбцов заданы признаки связи между соответствующими начальными и конечными вершинами трехмерного тела;

nx1, ny1 - массивы, содержащие значения координат вершин по оси X, Y;

ItemsCol - переменная, содержащая значение цвета.

Таким образом, в приведенном примене происходит следующее:

В цикле for перебираются все связи между вершинами. Номер текущей вершины хранится в переменной i.

Внутри цикла проверяется условие lm(fp(i), sp(i))=true, для проверки связи между вершинами с номерами fp(i), sp(i).

Если условие выполняется, производится вызов функции отображения линии на экране:

F_Line nx1(fp(i)), ny1(fp(i)), nx1(sp(i)), ny1(sp(i)), ItemsCol, 2,

на вход которой подаются требуемые параметры (значения координат, цвет, толщина линии).

---

В результате на экране появляется контур текущей проекции заданного трехмерного тела (рис. 1).

Рис.1 Пример отображения проекции трехмерного тела на экране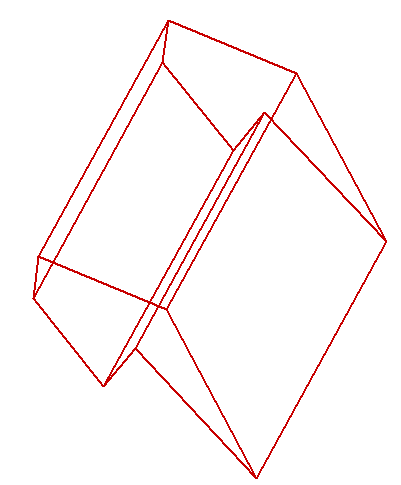

Практическая работа №4

Программирование геометрических уравнений на плоскости

Для отображения трехмерных тел на экране компьютера требуется построение проекций тел на плоскость экрана.

Различные проекции трехмерных тел могут быть результатом таких операций, как поворот и масштабирование.

Кроме этого, при отображении необходимо обеспечивать реалистичность получаемых проекций. Это достигается путем удаления с изображения проекции невидимых вершин и ребер.

Расчет новых координат вершин при повороте и масштабировании трехмерных тел и последующий анализ на наличие невидимых вершин и ребер требует применения определенного математического аппарата, включающий уравнения для геометрических преобразований на плоскости и в пространстве.

Уравнения на плоскости представляют собой следующие зависимости:

1. Уравнение прямой на плоскости;

2. Уравнение прямой, перпендикулярной заданной прямой;

3. Уравнение точки пересечения двух прямых на плоскости;

4. Формула определения расстояния между двумя точками.

Данные зависимости должны быть реализованы в программе в виде выражений, функций и подпрограмм, которые должны формировать результат на основе входных параметров.

Формулы зависимостей.

1. Уравнение прямой, проходящей через две точки

, b= y₁ -

x₁

y = kx + b,

.

k =

=>

=

y - y₁ x – x₁ y₂ - y₁ y₂ - y₁

y₂ - y₁ x₂ – x₁ x₂ – x₁ x₂ – x₁

2. Уравнение прямой, перпендикулярной другой прямой в точке (x_1, y₁)

y = kp ^.x + bp,

где:

kp = - 1/k,

bp = y₁ - kp ^.x₁,

k – угловой коэффициент исходной прямой.

Примечание: в программе необходимо учитывать случаи деления на 0 и производить отдельную обработку таких случаев.

3. Координаты точки пересечения двух прямых

x =

, y =

, где

b₁ – b₂ k₂ ^. b₁ – k₁ ^. b₂

k₂ – k₁ k₂ – k₁

b₁, k₁; b₂, k₂ – коэффициенты первой и второй прямой соответственно

4. Формула определения расстояния между двумя точками на плоскости

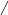
d = (x₁ - x₂)²+(y₁ - y₂)²

Средства языка программирования для записи математических выражений

В VBA имеются следующие операторы и функции для реализации приведенных выше зависимостей:

= - операция присваивания (слева приемник, справа - источник);

* - умножение;

/ - деление;

+ - сложение;

- - вычитание;

() - круглые скобки;

^ - возведение в степень;

Sqr() - функция вычисления квадратного корня

Например, выражение для расчета расстояния между двумя вершинами на языке VBA выглядит так:

d = Sqr((nx1(0) – nx1(1)) ^ 2 + (ny1(0) – ny1(1)) ^ 2),

где:

d – переменная вещественного типа, в которую записывается результат;

nx1(0) , ny1(0), nx1(1), ny1(1) – элементы массивов координат для первой и второй вершин.

Практическая работа №5

Программирование пространственных геометрических уравнений

---

Для отображения трехмерных тел на экране компьютера требуется построение проекций тел на плоскость экрана.

Различные проекции трехмерных тел могут быть результатом таких операций, как поворот и масштабирование.

Кроме этого, при отображении необходимо обеспечивать реалистичность получаемых проекций. Это достигается путем удаления с изображения проекции невидимых вершин и ребер.

Расчет новых координат вершин при повороте и масштабировании трехмерных тел и последующий анализ на наличие невидимых вершин и ребер требует применения определенного математического аппарата, включающий уравнения для геометрических преобразований на плоскости и в пространстве.

Уравнения в пространстве представляют собой следующие зависимости:

1. Уравнение плоскости в пространстве, проходящей через три точки;

2. Параметрическое уравнение прямой в пространстве;

3. Уравнение точки пересечения прямой и плоскости в пространстве;

4. Формула определения расстояния между двумя точками в пространстве.

Данные зависимости должны быть реализованы в программе в виде выражений, функций и подпрограмм, которые должны формировать результат на основе входных параметров.

Формулы зависимостей.

5. Уравнение плоскости в пространстве

Ax + By + Cz + D = 0

6. Уравнение плоскости в пространстве, проходящей через три точки

x -x₁ y-y₁ z-z₁

x₂-x₁ y₂-y₁ z₂-z_{1 = 0}

x₃-x₁ y₃-y₁ z₃-z₁

A = (y₂ - y₁) (z₃ - z₁) - (y₃ -y₁) (z₂ - z₁)

B = (z₂ - z₁) (x₃ - x₁) - (z₃ - z₁) (x₂ - x₁)

C = (x₂ - x₁) (y₃ - y₁) - (y₂ - y₁) (x₃ - x₁)

D = - (Ax₁ + By₁+ Cz₁)

7. Параметрическое уравнение прямой в пространстве

x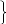 = αt + x₀

y = βt + y₀

z = γt + z₀

, где α, β, γ – координаты коллинеарного вектора, проведенного из начала координат.

8. Координаты точки пересечения прямой и плоскости в пространстве

x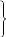 = αt + x₀

y = βt + y_{0 =>}

z = γt + z₀

Ax + By + Cz + D = 0

A

= > t = -

x₀ + By₀ + Cz₀ + D

Aα + Bβ + Cγ

Примечание: в программе необходимо учитывать случаи деления на 0 и производить отдельную обработку таких случаев.

9. Формула определения расстояния между двумя точками в пространстве

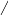
d = (x₁ - x₂)²+(y₁ - y₂)²+(z₁ - z₂)²

Средства языка программирования для записи математических выражений

В VBA имеются следующие операторы и функции для реализации приведенных выше зависимостей:

= - операция присваивания (слева приемник, справа - источник);

* - умножение;

/ - деление;

+ - сложение;

- - вычитание;

() - круглые скобки;

^ - возведение в степень;

Sqr() - функция вычисления квадратного корня

Например, выражение для расчета расстояния между двумя вершинами на языке VBA выглядит так:

d = Sqr((nx1(0) – nx1(1)) ^ 2 + (ny1(0) – ny1(1)) ^ 2) + (nz1(0) – nz1(1)) ^ 2),

где:

d – переменная вещественного типа, в которую записывается результат;

nx1(0) , ny1(0), nx1(1), ny1(1) , nz1(1), nz1(1) – элементы массивов координат для первой и второй вершин в пространстве.

Практическая работа №6

Создание проекций трехмерных тел

В результате операций поворота и масштабирования формируются различные проекции трехмерных тел, которые отображаются на экране.

---

Смотрите также файлы

• 09.03.03DS Информационные системы и технологии(кур.раб.).pdf

• Курсовая моделирование процессов и систем МУ.doc

• Контрольная по МСС для заочников.doc

• Пример семестровой Разработка программного средства.doc

• ЛР-3 (Excel - Поиск решения).doc