Файл: Лабы технологическая оснастка.docx

Анализ сил, действующих на рычаг.

Все силы, действующие на рычаг, создают многоугольник сил, изображенный на рис. 2 «б» . Для построения многоугольника сил на схеме выбирается свободное место и проводятся линии, параллельные направлениям действующих сил. В результате, получается треугольник основных сил R_W, R_N1 и S к которым пристраивают образующие силы трения и нормального давления с учетом углов трения. (рис.2 «б»).

Расчет сил, действующих на рычаг

Из рис. 2 «б» видно, что основные силы, действующие на рычаг, а именно R_W, R_N1 и S, образуют треугольник сил. В этом треугольнике известной силой является сила зажима детали – W, остальные силы нужно определить. Для определения неизвестных сил применяется теорема отношения сторон и углов треугольника:

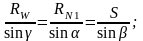
Из приведенного соотношения, с учетом того, что 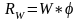, следует:

.

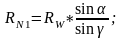
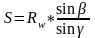Для решения задачи необходимо определить неизвестные углы в треугольнике сил. Углы в треугольнике сил определяются либо простым анализом сторон многоугольника с учетом геометрической формы рычага, либо с помощью дополнительных построений и соответствующих решений.

Угол β. На основании анализа многоугольника сил видно, что угол β

определяется из равенства:

β=180⁰-2φ-α_к;

Где, φ- угол трения;

α_к – угол наклона рабочей поверхности клина.

Для определения углов α и β или одного из них нужно установить положение силы S относительно силы R_N1 либо силы R_W. Из рисунка 2 «б» видно, что угол γ находится как разность углов:

γ = 90⁰-(90-α_к) –δ = α_к–δ.

Угол δ можно определить, если из полюса сил восставить перпендикуляр к левому плечу рычага (рис. 2 «а»). Тогда угол δ находится из выражения 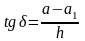(рис. 3) . Для о пределения параметров а₁ и h выполняется дополнительное построение – линия действия силы R_W продолжается, до пересечения с продолжением плеча b (т. О₁). Из анализа образовавшихся треугольников видно, что h=h₁ – мО, а мО находится из треугольника ОО₁к по зависимости 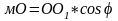. В свою очередь, ОО₁ определяется из треугольника ОО₁к по следующему выражению: 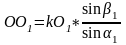. кО₁ = h₁ – b. где: 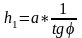; 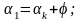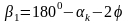. С учетом выше изложенного отрезок Ом определяется последующему выражению :

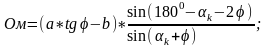
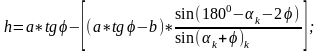
Найденное значение h позволяет найти значение отрезка а₁ плеча рычага;

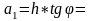
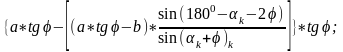
Тогда угол δ определяется следующим выражением:

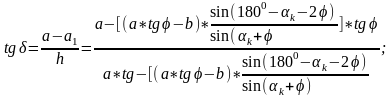
Полученное выражение позволяет определить угол γ =α_к + δ, а вместе с ним и все остальные неизвестные силы, действующие на рычаг – S и N_1, что позволяет приступить к расчету сил, действующих на клин.

Расчет сил, действующих на клин

Для расчета сил вычерчивается эскиз клина, определяются все, действующие на него силы, которые наносятся на звено, находящееся в рабочем положении, т.е. в положении зажатой детали (рис.4 «а»).

К основным силам относятся:

• R_{N1 -} равнодействующая сила в месте соединения клина с рычагом;

• R_N2 - равнодействующая сила в месте контакта клина с опорой;

• N₀ – сила, действующая на клин со стороны силового механизма.

---

Остальные силы – силы трения и силы нормального давления, от которых зависят равнодействующие, определяются в зависимости от конструктивных особенностей звеньев, их физико-механических свойств, условий работы и других факторов.

После определения сил и направлений их действия строится многоугольник сил, действующих на клин (рис.4 «б»), на котором обозначаются силы, с сохранением направления их действия, и обозначаются углы между силами – γ, β, α, φ и α_к.

За известную силу принимается сила R_N1, рассчитанная в ходе расчета сил, действующих на рычаг. Цель расчета – определить силы R_N2 и N₀.

Для расчета записывается теорема соотношения сторон и углов треугольника (теорема синусов), в соответствии с рис. 4 «б».

;

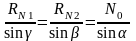Тогда: ; .

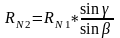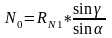Для определения неизвестных углов делается анализ схемы рис. 4 «а»,

из которого вытекает: ; ; .

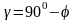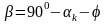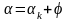Учитывая, что угол клина α_к задается конструктивно, а угол трения φ

зависит от физико-механических свойств контактирующих материалов и условий работы, сила N₀ , необходимая для расчета силового механизма можно считать определена.

СОДЕРЖАНИЕ И ПОСЛЕОВАТЕЛЬНОСТЬ

ВЫПОЛНЕНИЯ РАБОТЫ:

1. Вычертить схему механизма зажима детали с указанием направления силы зажима, конструктивных размеров звеньев и углов, определяющих положение звеньев механгизма..

2. Установить из каких простых звеньев состоит механизм зажима детали..

3. Вычертить схему первого звена механизма зажима и определить силы, образующиеся в его рабочем положении (положение зажатой детали)..

4. Определить положение полюса сил, действующих на первое звено (при необходимости)..

5. Построить многоугольник сил, действующих на первое звено механизма.

6. Сделать анализ сил и углов и определить зависимости составляющих сил от силы зажима W.

7. При необходимости, выполнить дополнительные построения с целью определения неизвестных данных для расчета сил..

8. Рассчитать неизвестные силы, действующие на первое звено механизма зажима.

9. Повторить пункты 3-8 для второго звена механизма зажима.

10. Повторить пункты 3-8 для третьего и последующих звеньев механизма зажима.

11. Сделать вывод

ЗАЧЕТ ПО ЛАБОРАТОРНОЙ РАБОТЕ

1.Зачет по лабораторной работе принимается только по представлению полностью оформленного отчета.

2.Для получения зачета студент должен подготовиться по содержанию лабораторной работы по следующим основным вопросам:

- Структура и назначение механизма зажима.

- Последовательность расчета механизма зажима.

- Определение положения полюса сил, действующих на звено механизма зажима.

- Особенности построения многоугольника сил

- Определение неизвестных сил в многоугольнике сил.

3. Зачет по лабораторной работе выставляется преподавателем, ведущим лабораторные работы, после собеседования со студентом, при условии, что он имеет четкое понимание и достаточные знания теоретического и учебного материала, использованного для лабораторной работы.

---

4. Если у преподавателя имеются существенные замечания по результатам работы и выполненная работа отложена на дополнительную доработку повторный зачет принимается в дополнительное, назначенное преподавателем, время.

БИБЛИОГРАФИЧЕСКИЙ СПИСОК

Кочин А.Н., Тудакова Н.М. Основы конструирования и расчета деталей станочных приспособлений. Нижегород. гос. техн. университет им. Р.Е. Алексеева. Н.Новгород, 2015.

Кочин А.Н., Фролова И.Н., Тудакова Н.М. Технологическая оснастка Часть 1 Комплекс учебно-методических материалов для студентов заочной и дистанцинной форм обучения. Нижегород. гос. техн. университет

Справочник технолога-машиностроителя. В 2-х т/ Под редакцией . Косиловой А.Г. и Мещерякова Р.К- 4-е изд., перераб., и доп.- М.: машиностроение. 1986.

.

Нижегородский Государственный технический университет Р.Е.Алексеева

Институт промышленных технологий машиностроения

Кафедра «Технология и оборудование машиностроения»

Дисциплина «Технологическая оснастка»

ЛАБОРАТОРНАЯ РАБОТА № 8

РАСЧЕТ ПРИСПОСОБЛЕНИЯ НА ТОЧНОСТЬ

г. Нижний Новгород 2017

ЦЕЛЬ РАБОТЫ:

Выполнить расчет точности заданного в технологическом процессе обработки детали приспособления.

ИСХОДНЫЕ ДАННЫЕ:

Технический чертеж станочного приспособления, технологическая операция, модель металлорежущего станка..

РАСЧЕТ ТОЧНОСТИ ПРИСПОСОБЛЕНИЯ

Расчет точности приспособления заключается в решении двух задач:

1. Выполняение условий точности установки ε_у детали на разработанном или проверяемом приспособлении.

2. Определение расчетной суммарной погрешности разработанного или проверяемого приспособления Δ_Σ .

Выполняение условий точности установки ε_у детали

Основным условием расчета точности приспособления является требование, которое заключается в получении при обработке детали погрешности установки ε_у не превышающей допустимую погрешность установки ε _удоп.

Таким образом, для решения поставленной задачи необходимо определить действительную погрешность установки ε_у, получаемую при базировании детали на заданном или разработанном приспособлении. Кроме того, нужно определить допустимую погрешность установки ε_удоп, которая может быть получена при выполнении заданной технологической операции с учетом всех образующихся погрешностей. Приспособление можно считать удовлетворяющим требованиям точности, если ε_у ≤ ε_удоп.

Действительная погрешность установки ε_у определяется анализом и расчетом полученных в ходе проектирования или проверки процесса установки обрабатываемой детали на приспособлении по зависимости:

ε_у =

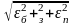
Где ε_б - погрешность базирования детали на приспособлении (получается расчетом, см. лаб.раб. №3)

ε_з - погрешность закрепления детали на приспособлении

---

(расчет погрешности лаб.раб. №6)

ε_п – погрешность положения (приспособления) зависит от изготовления деталей приспособления, сборки, износа приспособления, его установки на рабочем месте и других факторов (определяется при обработке партии деталей и может устранятся наладкой). В лабораторной работе ε_п=0.

Таким образом, в лабораторной работе действительную погрешность установки ε_у можно определить по упрощенной зависимости:

ε_у =

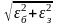
Допустимая погрешность базирования ε_уоп определяется в зависимости от условий обработки детали на заданной технологической операции с учетом всех основных технологических факторов, в зависимости от допуска на получаемый на операции размер Т и средняя экономическая точнсть обработки детали на заданной операции.

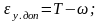
Где: ω – средняя экономическая точность выполняемой технологической операции (например, точение предварительное, берется по справочнику);

Т - допуска на выполняемый размер.

Расчетной суммарной погрешности разработанного или проверяемого приспособления Δ_Σ определяется по зависимости:

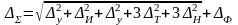
Где : ∆_у -погрешность вследствие упругих отжатий технологической системы под влиянием сил резания (погрешность деформации);

∆_Н – погрешность настройки станка в ненагруженном состоянии;

Δ_у – погрешность установки приспособления на столе станка;

∆_И –погрешность от размерного изнашивания инструмента;

∆_Т – погрешность обработки, вызываемая тепловыми деформациями технологической системы;

∆_ф – суммарная погрешность формы обрабатываемой поверхности,

обусловленная геометрическими погрешностями станка и деформацией заготовки при обработке (выбирается из таблицы, в зависимости от номинального значения и точности получаемого размера) ;

Δ_Σ - допуск обрабатываемой на технологической операции детали;

Следовательно, суммарная погрешность приспособления, исходя из вышеприведенной зависимости, определяется:

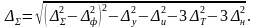
_{В этом уравнении Δу, Δи. Δт и Δн характеризуют суммарный расход поля допуска при обработке партии деталей на металлорежущем станке за период наладки режущего инструмента до его затупления.}

Определение погрешности детали, вызванной упругими деформациями технологической системы «j».

Упругие отжатия (деформации) элементов технологической системы – металлорежущего станка, приспособления, режущего инструмента и обрабатываемой детали, происходят под действием сил резания, возникающих в процессе обработки. Величина упругих перемещений элементов технологической системы зависит не только от сил резания, но и от жесткости элементов системы. Жесткостью называют способность элементов технологической системы сопротивляться действию на неё силовых факторов. Единица измерения жесткости – ньютон на миллиметр.

---

Жесткость определяется как отношение составляющей силы Р_у  к смещению у  в направлении действия силы, т.е.

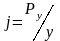Н/мкм

В технологических расчетах часто пользуются таким понятием, как податливость, определяемой для статических условий, как упругое перемещение технологической системы, вызываемое силой, равной единице, т.е. как величиной, обратной жесткости –

.

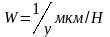Погрешность обработки, вызванная упругими отжатиями технологической системы будет определятся по зависимости;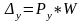 мкм/Н

  Р_у - составляющая силы резания, оказывающая основное влияние на точность обработки наружной цилиндрической поверхности, обрабатываемой точением. Величину составляющей силы резания можно определить, используя формулы теории резания. При точении, например, наружных цилиндрических поверхностей сила резания Р определяется следующей зависимостью:

Р = 10 С_р t^x S^уVⁿ k_р :

Где – t,S, V – режим обработки детали;

x, y, n – показатели степени;

k_p - коэффициент, зависящий от условий обработки.

Величина упругих отжатий (деформаций) у технологической системы величина не стабильная и зависит от многочисленных факторов – изношенности технологического оборудования, способа установки заготовки в приспособлении, жесткости самой обрабатываемой заготовки, жесткости режущего инструмента и т.д., и определяется экспериментально. Например, при точении вала «1» режущий инструмент «2» настраивается на глубину резания, «t_з» (рис. 1 а), а после обработки вала (рис. 1 б) глубина резания вследствие деформации технологической системы оказалась меньше заданной на величину Δ t = t_з – t_ф, где t_ф – фактически полученная глубина резания. В этом случае, жесткость технологической системы определяется по следующей зависимости: 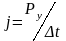, где Δt- определяет деформацию технологической системы.

Определение погрешности детали, вызванной износом режущего инструмента «ΔU».

Износ режущего инструмента ΔU, это изменение размера режущего клина, вызванное «истиранием» его задней поверхности в процессе обработки детали. Погрешность детали, вызванная износом режущего инструмента, образуется за счет увеличения размера обработанной поверхности (размера обрабатываемых деталей) на величину образовавшегося износа (рис. 2 «а»). Изнашивание режущего инструмента происходит неравномерно и зависит от количества обработанных деталей – длина пути резания L. При изучении влияния износа рассматриваются три основных периода:

- период начального износа режущего инструмента (приработка);

- период нормального износа (эффективной работы режущего инструмента);

- период разрушения режущего инструмента.

ΔU

Графическая зависимость износа режущего инструмента ΔU от длины пути резания L, показывает, что величина износа для каждого периода изменяется по различным закономерностям, и, следовательно, не будет постоянной величиной и зависит только от технологических факторов.

---