ВУЗ: Санкт-Петербургский государственный лесотехнический университет имени С.М.Кирова
Категория: Методичка
Дисциплина: Технические измерения и приборы
Добавлен: 15.11.2018
Просмотров: 3395
Скачиваний: 23

чину
max
в
δ
z′
, откуда затем определим
в
z′
.
С достаточной для практики точностью можно принимать
t
z
z
z
=
′′′
=
′′
=
′
в
в
в
.
Аналогично, по известному значению
max
в
δ
z ′′
по графику (
рис. 1.5
)
оп-
ределяем величину
max
δ
x ′′
, откуда затем определим х″.
4.2. Определяем проводимости отдельных фигур, показанных на
рис.
1.4,
в соответствии с выражениями
табл. 1.3.
Магнитную проводимость
воздушных зазоров определяем как сумму их составляющих.
Для зазора δ
IV
G
δ IV
= 3 G
1
+ 3 G
2
+ 2 G
3
+ 2 G
4
+ G
5
+ G
7
+ 4 (G
3
+ G
4
).
Магнитное сопротивление зазора δ
IV
IV
δ
IV
δ
1
G
R
=
.
Для зазора δ
II
G
δ II
= 2G
1
+ 2 G
2
+ G
5
+ G
6
+ G
7
+ 4 (G
3
+G
4
).
Магнитное сопротивление зазора
II
δ
II
δ
1
G
R
=
.
Суммарное магнитное сопротивление одной половины магнитной це-
пи преобразователя определяем по формуле (1.1). Суммарное магнитное
сопротивление всей цепи определяем из выражения (1.2).
11
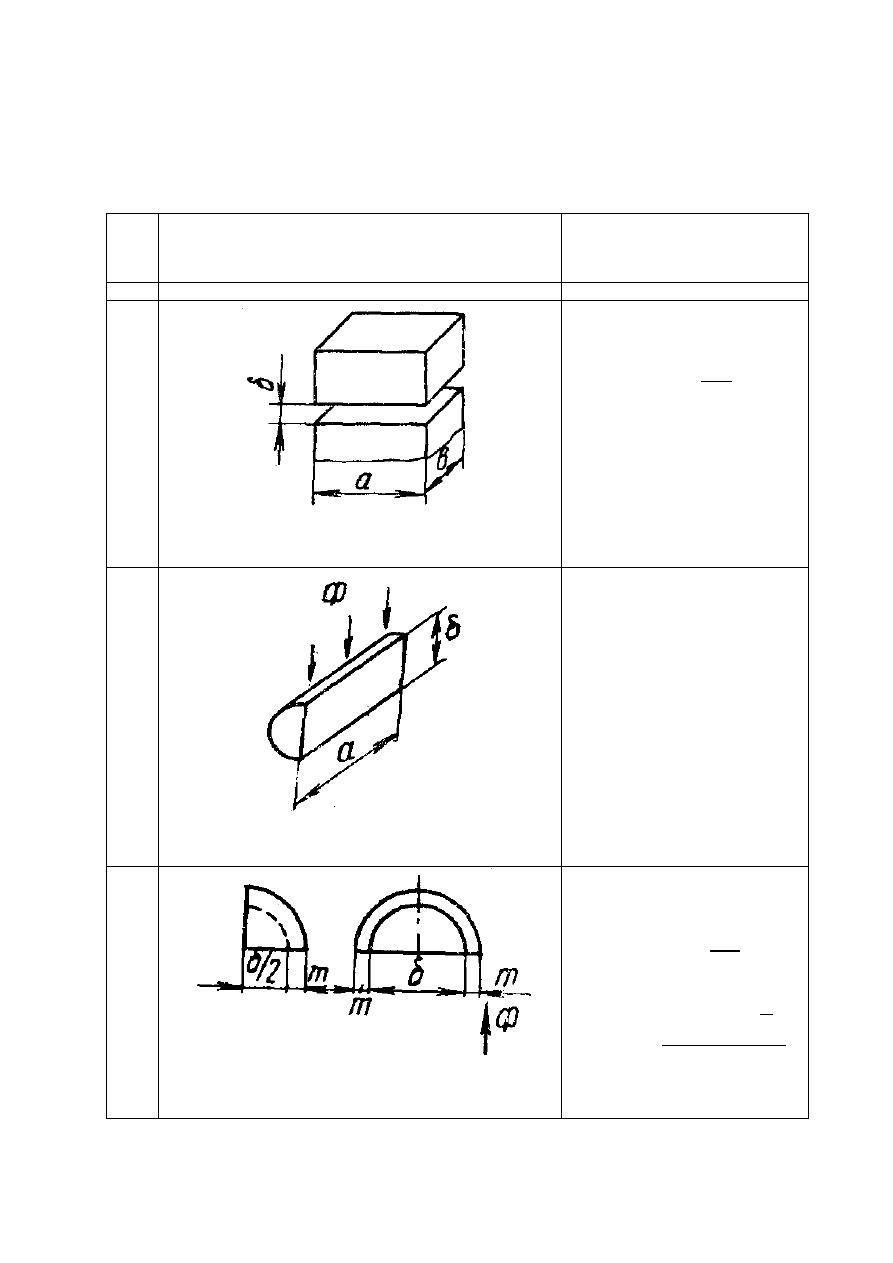
Таблица 1.3
Основные формулы магнитного поля и аналитическое выражение
их магнитных проводимостей
№
п/п
Эскиз объемной фигуры магнитного поля
Формула магнитной
проводимости
1
2
3
1
Прямоугольный параллелепипед
δ
μ
o
3
b
a
G
=
,
где μ
о
= 1,26 · 10
‒6
Г/м
2
Полуцилиндр
G
4
= 0,26
μ
о
a
3
Квадрант сферической оболочки
4
μ
1
o
7
m
G
=
,
где
2
2
δ
в
1
−
′′
+
′
=
х
z
m
12
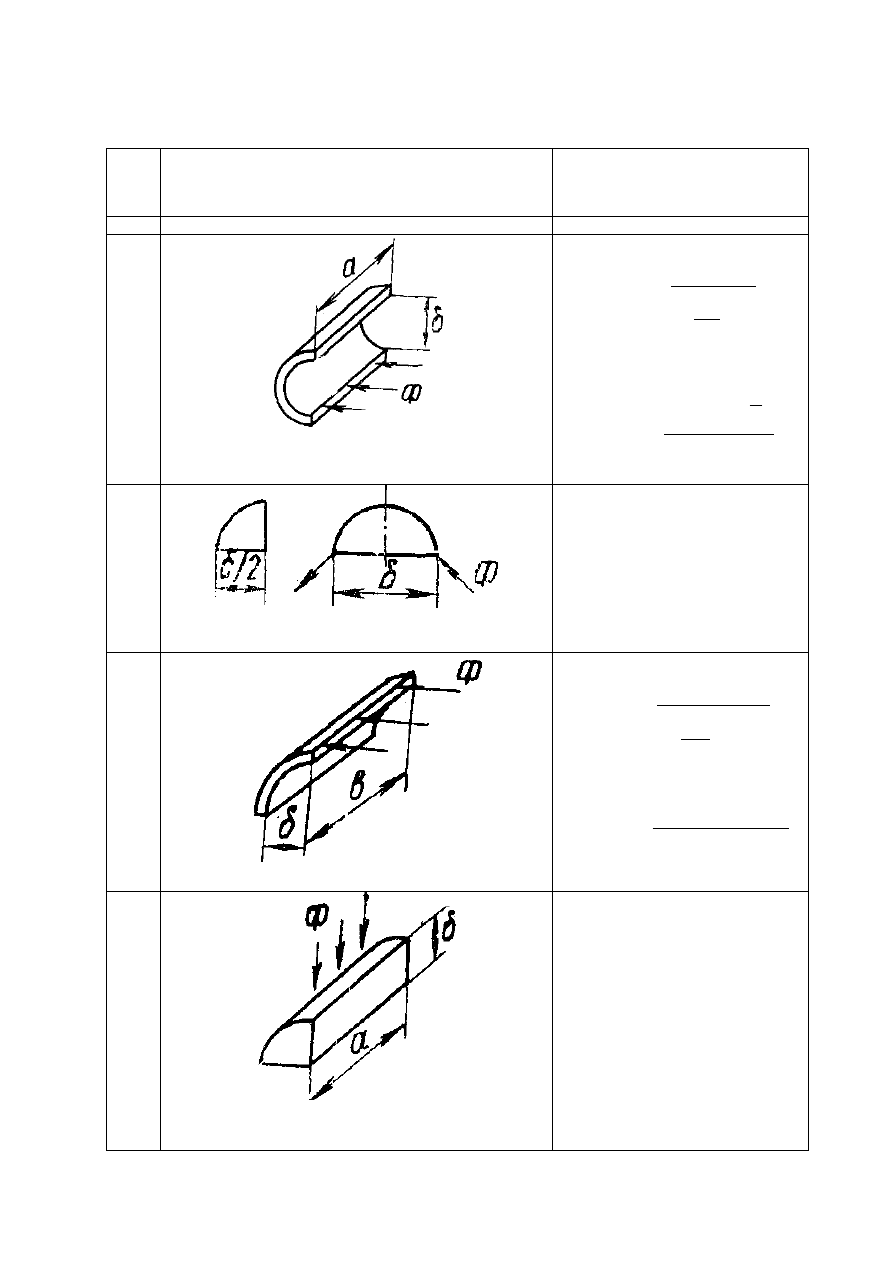
Продолжение табл. 1.3
№
п/п
Эскиз объемной фигуры магнитного поля
Формула магнитной
проводимости
1
2
3
4
Половина полого цилиндра
+
=
1
δ
π
2
μ
1
o
5
m
a
G
,
где
2
2
δ
в
1
−
′′
+
′
=
х
z
m
5
Сферический квадрант
G
6
= 0,077
μ
о
δ
6
Четверть пологого цилиндра
+
=
5
,
0
δ
π
2
μ
2
o
1
m
b
G
,
где
(
)
2
δ
max
в
2
−
′
+
′
=
х
z
m
7
Четверть цилиндра
G
2
= 0,52
μ
о
a
13
5. Зная
Σ
м
R
,
определяем электрическое сопротивление катушки z
э
:
Σ
м
2
а
э
ω
R
W
R
z
⋅
+
=
,
где R
а
–
активное сопротивление катушки, Ом; ω = 2π f – круговая частота,
где f – частота, Гц, для
курсового проекта
принять f = 50 Гц.
W
q
l
R
ср
a
ρ
=
,
где ρ – удельное сопротивление медной проволоки, ρ = 0,0175 Ом · мм
2
/м;
l
ср
–
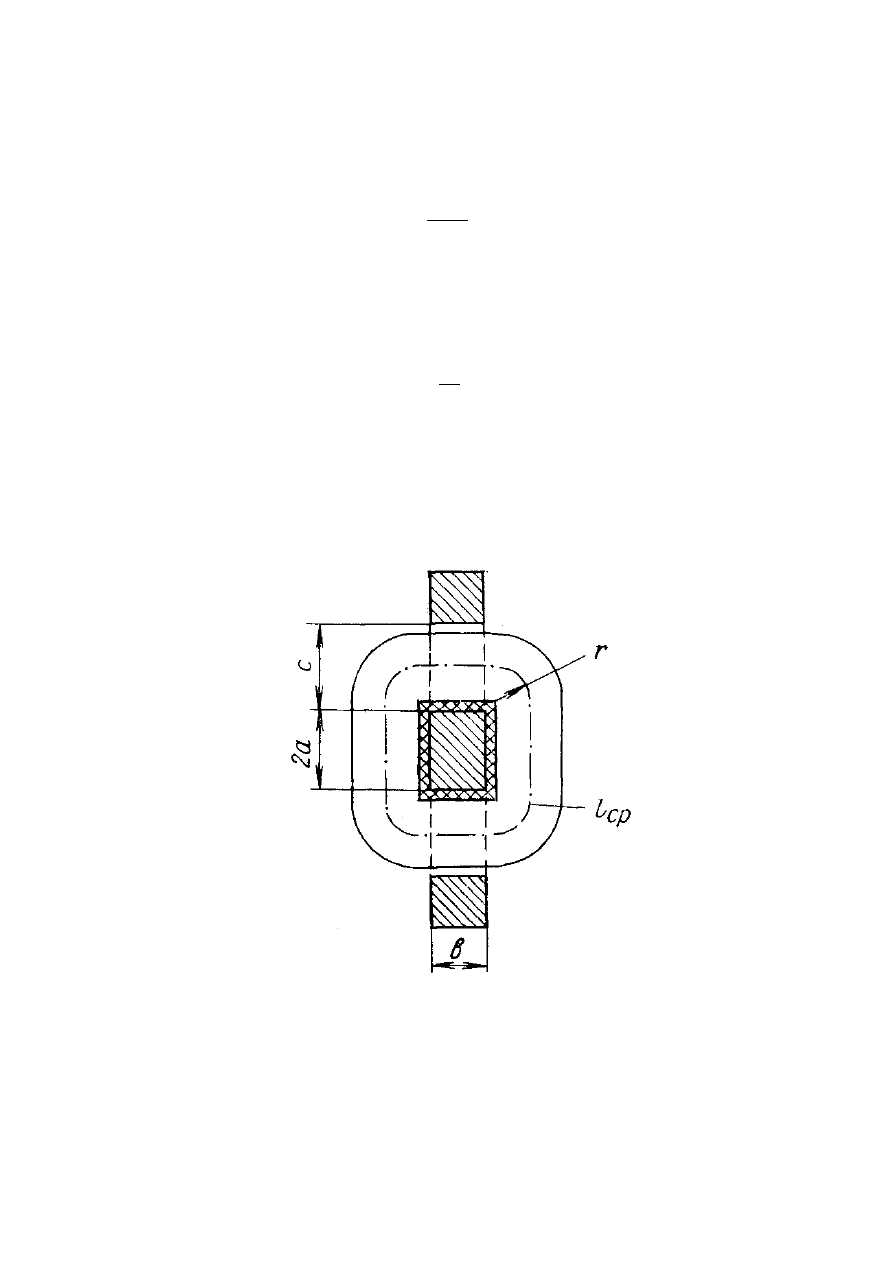
средняя длина витка, м (
рис. 1.6
), l
ср
= 4
а + 2 b + 2π r; g – поперечное
сечение голого провода, мм
2
, выбираем по
табл. 1.2
для принятого диамет-
ра провода.
Рис. 1.6. Сечение индуктивного преобразователя
Модуль электрического сопротивления определяем из выражения
14

2
Σ
м
2
a
э
ω
+
=
R
W
R
z
.
6.
Определяем эффективное значение тока через катушку, необходи-
мого для создания выбранной магнитной индукции В:
2
Σ
м
W
R
Ф
I
Σ
=
,
где Ф
∑
‒ магнитный поток в сердечнике, Ф
∑
=
В · S, Т · м
2
; S –
площадь се-
чения среднего сердечника, м
2
.
7.
Проверяем катушку на допустимую плотность тока. Рекомендуется
плотность тока
5
,
2
...
2
≤
=
q
l
j
А/мм
2
.
8.
Определяем напряжение питания катушки:
U = I z
э
, В.
9. Определяем чувствительность преобразователя. Для этого необхо-
димо определить сопротивление магнитной цепи
Σ
′
м
R
и электрическое со-
противление катушки z′
э
при наименьшем зазоре δ
min
:
2
Δδ
δ
δ
o
min
−
=
.
Аналогично п. 4.1 находим z′
в
и х″ для δ
min
. Далее выполняем расчеты
по п.п. 4.2, 5.6, в результате которых получаем новые значения
∗
Σ
м
R
,
∗
э
z
, I
*
.
Таким образом, при изменении зазора на величину Δδ сопротивление ка-
тушки изменилось на величину
э
э
э
z
z
z
−
=
∆
∗
.
Считая, что чувствительность во всем диапазоне измерения постоян-
на, получаем
15