ВУЗ: Санкт-Петербургский государственный лесотехнический университет имени С.М.Кирова
Категория: Методичка
Дисциплина: Технические измерения и приборы
Добавлен: 15.11.2018
Просмотров: 3383
Скачиваний: 23

5.5.
Вычисляют разности x
n–j+1
– x
j
для каждого j и записывают их в
шестую графу
табл. 3.2
. Например, для n = 10 и j = 5 необходимо вычис-
лить разность x
10–5+1
= x
6
– x
5
,
для j = 4 вычисляют (разность х
7
–
х
4
, для j = 3
–
разность х
8
–
х
3
и т. д. Эти разности записываются напротив соответст-
вующего значения j.
5.6.
В седьмую графу
табл. 3.2
записывают значения произведений
a
n–j+1
· (x
n–j+1
– x
j
)
, т. е. произведение граф (5) и (6) для j = 1, 2,…,l (l = 1…5).
5.7.
Данные второй, третьей и седьмой граф суммируются и записы-
ваются в последнюю строчку этой таблицы.
5.8. При помощи сумм, установленных по п. 5.7, вычисляют характе-
ристики
n
x
x
n
i
i
n
i
i
2
1
1
2
2
−
=
∑
∑
=
=
ϕ
;
2
1
1
1
2
)
(
−
⋅
=
∑
=
+
−
+
−
l
j
j
j
n
j
n
x
x
a
b
.
5.9.
Вычисляют значение критерия проверки W по формуле
2
2
ϕ
b
W
=
.
5.10.
По
табл. 3.4
устанавливают, что вероятности a = 0,05 соответст-
вует для n = 10 величина W* = 0,842. Следовательно, вероятность того, что
вычисленное значение W будет менее W*, равна α, и критическую область
образуют все значения W < W*. Следовательно, если W ≥ W*, то нет осно-
вания для опровержения гипотезы, что опытное распределение для данных
условий является нормальным.
Уровень значимости α выбирают по
последней цифре зачетной книж-
ки
. В случае опровержения, гипотезы о нормальности распределения необ-
ходимо определить уровень значимости, при котором эта гипотеза может
быть принята.
6. Определяют наличие грубых погрешностей и промахов (анормаль-
ных результатов). Если последние обнаружены, вычисления повторяют.
Оценку анормальности результатов осуществляют в соответствии со
стандартом СТ СЭВ 545-77 для результатов наблюдений случайной вели-
чины, подчиняющейся нормальному закону распределения. Из
табл. 3.2
с
упорядоченной выборкой сомнительными могут быть наибольшее х
10
и
наименьшее значение х
1
.
36
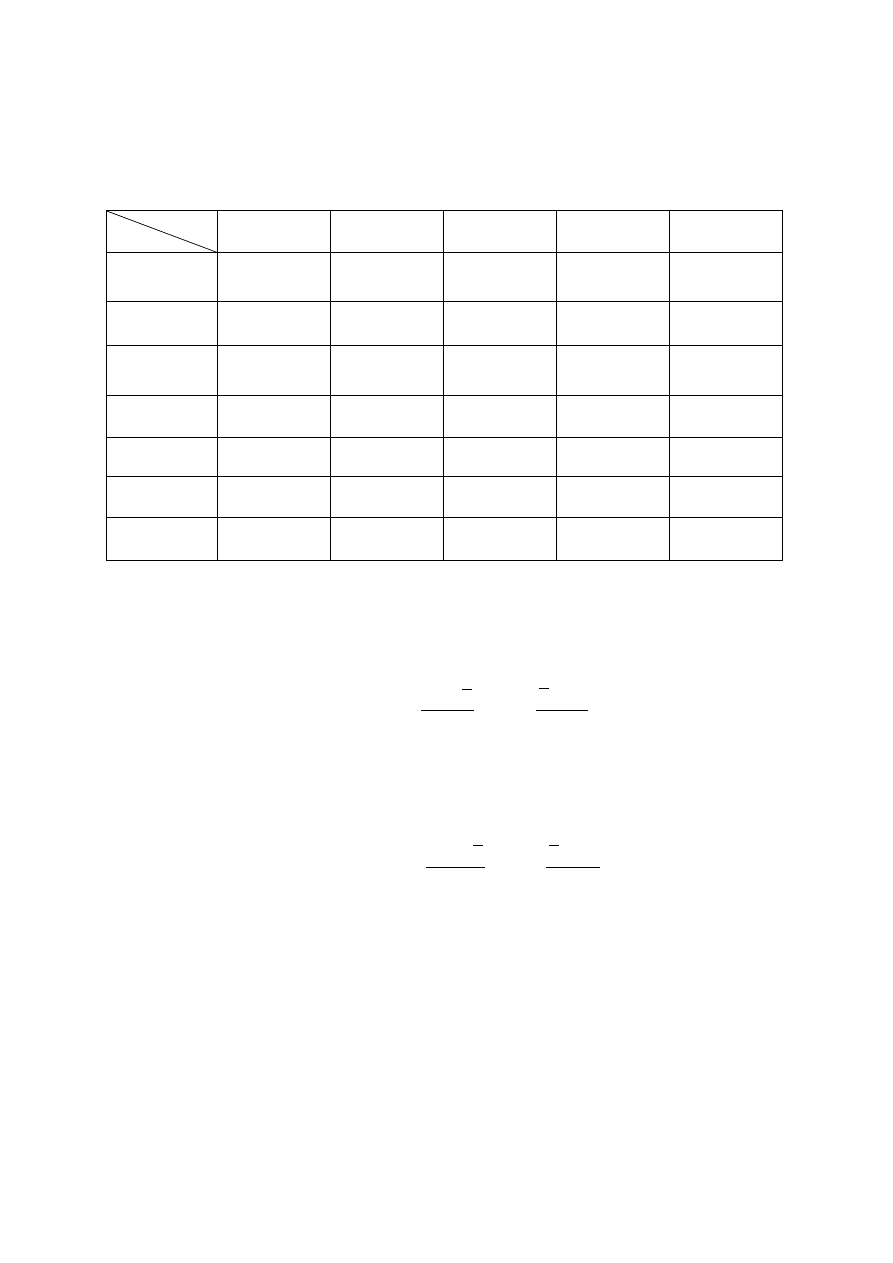
Таблица 3.4
Квантили распределения проверочного критерия нормальности W
для n = 5…10
α
п
0,01
0,02
0,05
0,10
0,50
5
0,868
0,715
0,762
0,806
0,927
6
0,713
0J43
0,788
0,826
0,927
7
0,730
0,760
0,803
0,838
0,928
8
0,749
0,778
0,818
0,851
0,932
9
0,764
0,791
0,829
0,859
0,935
10
0,781
0,806
0,842
0,869
0,938
Номер
варианта
0,9
1,8
2,7
3,6
4,5
Чтобы оценить принадлежность х
n
и x
1
к данной нормальной совокуп-
ности и принять решение об исключении или оставлении х
n
(x
1
)
, в составе
выборки находят отношение
x
n
S
x
x
U
−
=
n
;
x
S
x
x
U
1
1
−
=
.
Поскольку сомнительными являются х
10
и x
1
, то эти выражения при-
нимают вид
x
S
x
x
U
−
=
10
10
;
x
S
x
x
U
1
1
−
=
Результат U
n
и U
1
сравнивают с величиной h, взятой из
табл. 3.5.
для
своего варианта.
Если U
n
≥ h (или U
1
≥ h), то подозреваемый в анормальности результат
наблюдений должен быть исключен, а вычисления должны быть повторе-
ны с начала
задачи 3.
37

Таблица 3.5
Предельное значение h для случая неизвестного генерального среднеквадра-
тичного отклонения σ
х
№
п/п
Объем
выборок
Предельное значение при вероятности
0,01
0,075
0,050
0,025
1
2
3
4
5
6
1
5
1,60
1,64
1,67
1,72
2
6
1,73
1,77
1,82
1,89
3
7
1,83
1,88
1,94
2,02
4
8
1,91
1,96
2,03
2,13
5
9
1,98
2,04
2,11
2,21
6
10
2,03
2,10
2,18
2,29
Номер
варианта
от 5 до 9
от 0 до 4
7. Определяем доверительные интервалы для параметров нормального
распределения.
7.1. Доверительные границы ε (без учета знака) случайной погрешно-
сти результата измерения находят по формуле
x
S
t
=
ε
,
где t – коэффициент Стьюдента, который в зависимости от доверительной
вероятности р и числа результатов наблюдений находят в
табл. 3.6.
Записываем результат измерения в виде
...)
;
...
ε
(
...
±
=
±
=
=
р
x
7.2. Доверительные границы для среднего квадратического отклоне-
ния определяют в соответствии со стандартом СТ СЭВ 876-78.
При заданной доверительной вероятности нижнюю доверительную
границу определяют по формуле
S
x
н
= z
н
S
x
.
Верхнюю доверительную границу определяют по формуле
S
x
в
= z
в
S
x
.
38
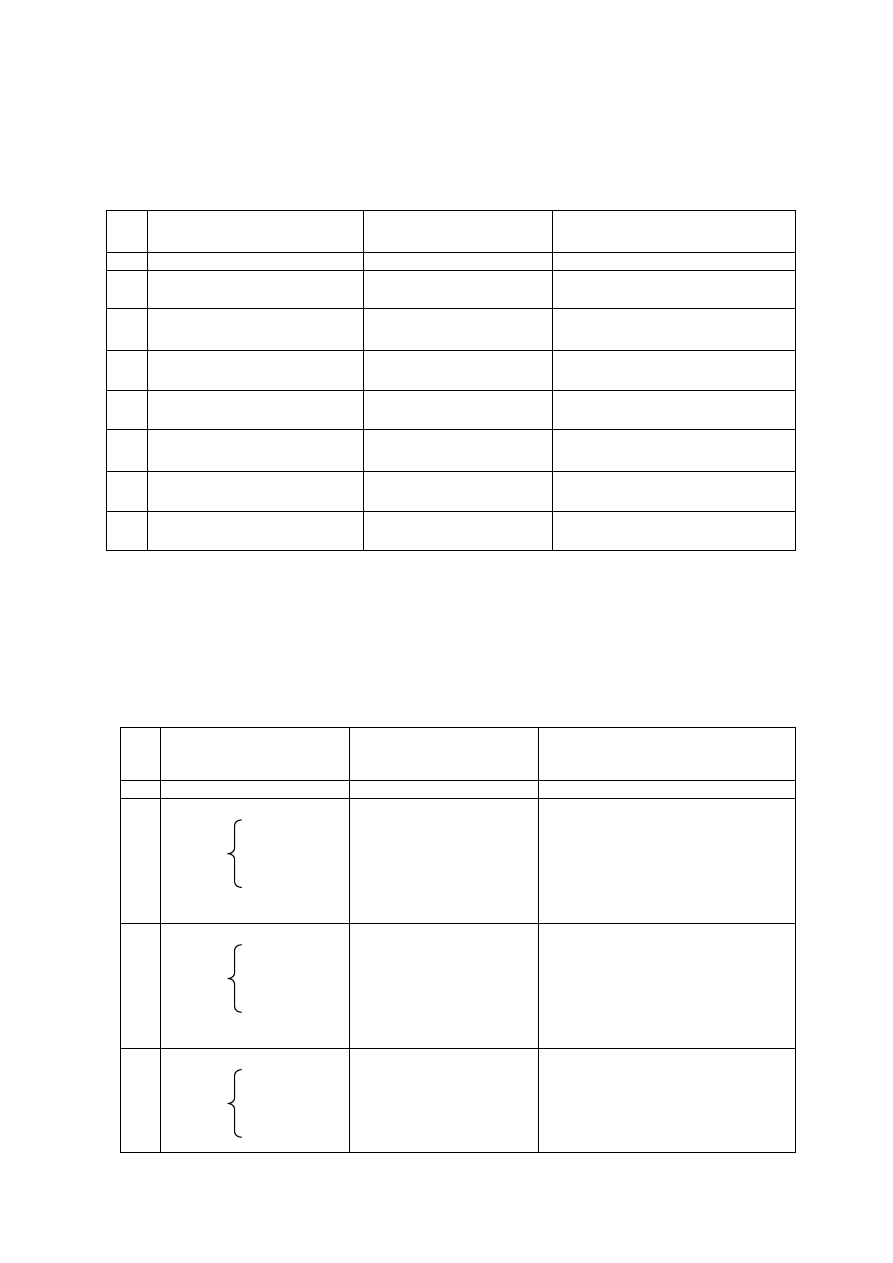
Таблица 3.6
Значения коэффициента t для случайной величины,
имеющей распределение Стьюдента
№
п/п
n – 1
t
p
= 0,95
t
p
= 0,99
1
2
3
4
1
5
2,571
4,032
2
6
2,447
3,707
3
7
2,365
3,499
4
8
2,306
3,355
5
9
2,262
3,250
6
10
2,228
3,169
Номер варианта
9-5
4-0
Значения z
н
и z
в
зависят от величины выборки и выбираются из
табл.
3.7
для заданной доверительной вероятности.
Таблица 3.7
Значения коэффициентов z
н
и z
в
№
п/п
р
0,95
0,99
1
2
3
4
1
z
н
n = 10
z
в
0,69
1,83
0,62
2,28
2
z
н
n = 9
z
в
0,68
1,92
0,60
2,44
3
z
н
n = 8
z
в
0,63
2,04
0,59
2,6
39

Среднеквадратическое значение находится в интервале
S
x
н
≤ S
x
≤ S
x
в
.
4.
Технологические измерения параметров
производственных процессов
На основании изучения конкретного технологического процесса и
технических характеристик оборудования по литературным источникам
сформулировать требования к средству измерения одного из технологиче-
ских параметров согласно варианту.
Определить или задаться пределами изменения измерительной вели-
чины и значениями погрешностей измерения целесообразными для данных
условий.
Сформулировать требования к конструктивному исполнению измери-
тельного устройства. В процессе решения задачи сначала анализируются
типовые ее решения по справочной литературе. При отсутствии типовых
решений дается сравнительный анализ методов и средств, известных из
специальной технической литературы, и выбирается наиболее подходящая
задача. Необходимо привести принципиальную электрическую схему из-
мерительного устройства в соответствии с требованиями ЕСКД и дать ее
подробное описание.
Номер варианта брать по последней цифре зачетной
книжки.
Варианты задания
1. Средства измерений объемов круглых лесоматериалов весовым ме-
тодом (на железнодорожном транспорте, на кранах и др.).
2.
Средства поштучного измерения линейных размеров и объема ле-
соматериалов (в составе линий разделки, сортировки или самостоятельно).
3.
Средства геометрического обмера пакетов лесоматериалов по габа-
ритным размерам (в составе устройств для определения объема партии
сортамента).
4.
Средства измерений перемещений и положения узлов технологиче-
ского оборудования (в составе манипуляторов, роботов и т. д.).
5.
Средства измерения сил и деформаций в конструкциях (в техноло-
гических конструкциях, подъемно-транспортных машинах и т. д.).
6.
Средства дефектоскопии древесины (в составе линий раскряжевки,
сортировки).
7.
Средства контроля режимов обработки древесины (скорость подачи,
резания и др.).
40