ВУЗ: Санкт-Петербургский государственный лесотехнический университет имени С.М.Кирова
Категория: Методичка
Дисциплина: Технические измерения и приборы
Добавлен: 15.11.2018
Просмотров: 3399
Скачиваний: 23

R
3
+ R
t min
=
η
o
(R
3
+ R
t max
),
где η
o
= 0,8…0,9,
тогда
o
min
o
max
3
η
1
η
−
−
=
t
t
R
R
R
.
Принимаем R
2
= R
3
.
3.
Определяем величину резистора R
п
.
При положении движка реохорда в крайнем правом положении, когда
R
t
= R
t min
,
условие равновесия мостовой схемы имеет вид
(R
t min
+ R
л
+ R
д
+ R
пр
) R
2
= (R
1
+ R
л
) R
3
.
(2.1)
При другом крайнем положении движка реохорда, когда R
t
= R
t max
,
ус-
ловие равновесия имеет вид
(R
t max
+ R
л
+ R
д
) R
2
= (R
2
+ R
пр
) (R
1
+ R
л
).
(2.2)
Вычитая из выражения (2.1) уравнение (2.2), получаем
3
2
1
min
max
2
пр
)
(
R
R
R
R
R
R
R
t
t
+
+
−
=
,
(2.3)
где R
пр
–
приведенное сопротивление реохорда,
экв
п
экв
о
пр
R
R
R
R
R
−
=
.
Для учета небольших нерабочих участков на краях реохорда вводим
коэффициент запаса λ = 1,064, который увеличивает R
пр
на 6,4 % – по 3,2 %
с каждой стороны реохорда:
R
′
пр
= R
пр
λ.
После преобразования получаем
пр
экв
экв
пр
o
R
R
R
R
R
−
′
=
26

4. Определяем величину резистора R
1
. Для этого подставляем выраже-
ние (2.3) в уравнение (2.1):
3
л
1
2
л
2
1
min
max
д
л
min
2
)
(
)
(
R
R
R
R
R
R
R
R
R
R
R
R
R
t
t
t
+
=
⋅
+
+
−
+
+
+
.
Так как R
2
= R
3
, уравнение имеет вид
л
1
л
2
1
min
2
max
2
д
л
min
R
R
R
R
R
R
R
R
R
R
R
R
t
t
t
+
=
+
+
−
+
+
⋅
+
.
После преобразований получаем
0
)
(
л
д
2
max
л
д
л
min
л
2
1
2
1
=
−
−
−
−
−
+
+
R
R
R
R
R
R
R
R
R
R
R
R
t
t
.
(2.4)
Решая уравнение (2.4) относительно R
1
аналогично решению обычно-
го квадратного уравнения, получаем
±
−
+
−
−
=
)
(
2
1
д
л
min
2
1
R
R
R
R
R
t
)
(
4
)
(
2
1
л
д
2
max
л
min
2
д
2
д
л
min
2
R
R
R
R
R
R
R
R
R
R
R
R
t
t
t
+
+
+
+
−
+
−
±
.
5. Рассчитываем балластное сопротивление R
б
из условия, чтобы мак-
симальный ток I
max
, проходящий через термометр сопротивления, не пре-
вышал 7 мА. При расчете считаем, что через R
б
протекает примерно удво-
енный ток верхней половины моста:
V
R
R
R
R
R
I
R
I
=
′
+
+
+
+
+
)
(
2
пр
3
л
д
min
1
max
б
max
,
откуда
max
пр
л
д
min
max
б
2
)
(
I
R
R
R
R
I
U
R
t
′
+
+
+
−
=
,
где V = 6,3 B – напряжение питания моста.
27
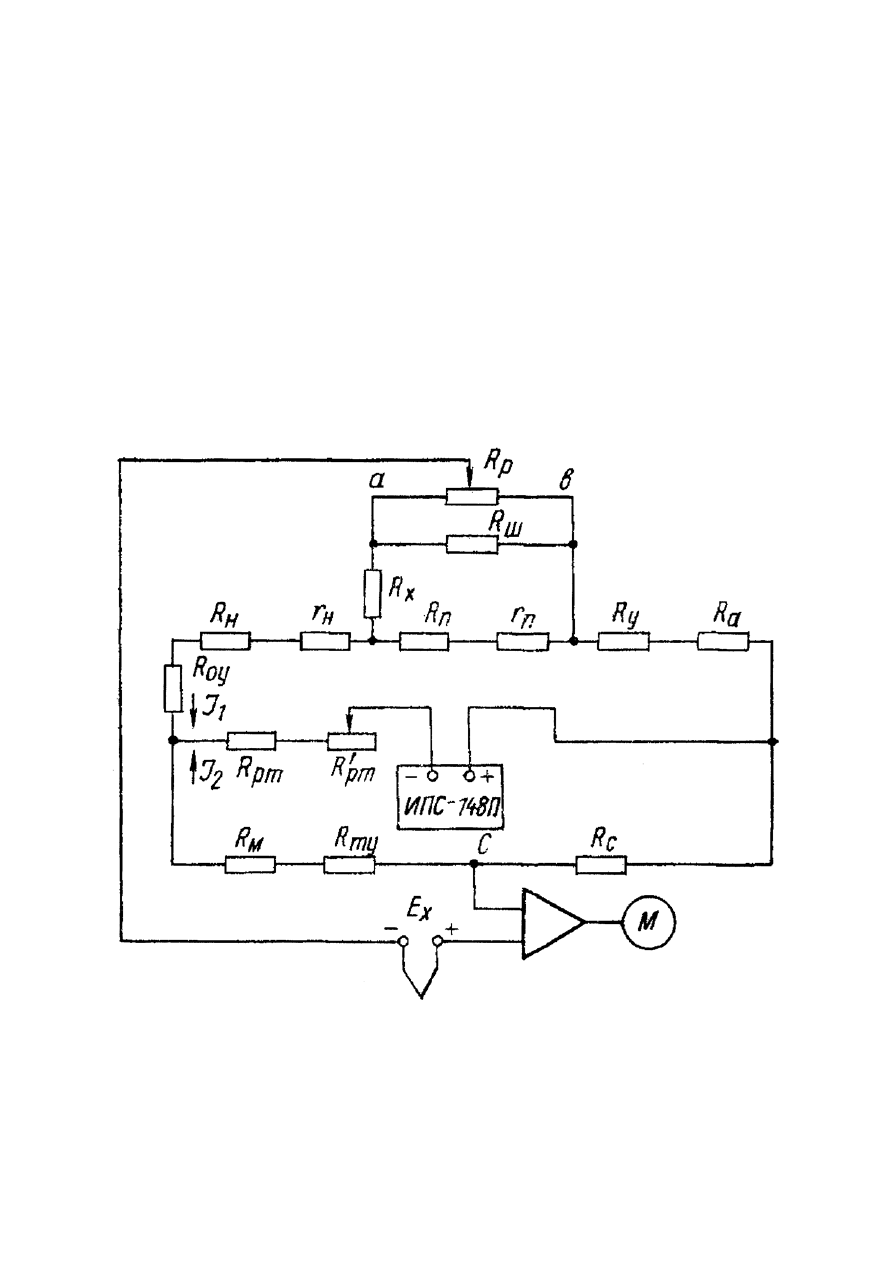
2.2. Потенциометрическая измерительная схема
Автоматические потенциометры предназначены для измерения и за-
писи температуры и других величин, изменения значений которых могут
быть преобразованы в изменения напряжения постоянного тока. Наиболее
часто автоматические потенциометры работают в комплекте с термоэлек-
трическими термометрами или радиационными пирометрами. В автомати-
ческих потенциометрах измерение производится методом компенсации
путем сравнения неизвестной термоэлектродвижущей силы (
ТЭДС),
соз-
даваемой термоэлектрическим термометром, с падением напряжения на
калиброванном реохорде. На
рис. 2.2
приведена измерительная схема ав-
томатического потенциометра КСП4, являющаяся типовой для измерения
ЭДС
или напряжений.
Рис. 2.2. Измерительная схема автоматического потенциометра
Схема состоит из резисторов, имеющих следующее назначение:
R
p
–
реохорд;
R
ш
–
резистор шунта;
28

R
п
—
резистор для задания предела измерения;
R
н
–
резистор для задания начала шкалы прибора;
r
н
; r
п
–
подгоночные резисторы;
R
м
–
вспомогательный резистор, выполненный из меди, для потенцио-
метров с компенсацией
ТЭДС
свободных концов и из манганина для по-
тенциометров и миллиамперметров без компенсации. Располагается вбли-
зи зажимов термоэлектрического термометра, поэтому температура рези-
стора равна температуре свободных концов;
R
рм
; R
′
рм
–
резисторы для ограничения и регулировки рабочего тока
источника питания;
R
а
–
балластный резистор, служит для ограничения тока в измеритель-
ной схеме;
R
с
–
резистор для контроля рабочего тока;
R
х
; R
y
; R
oy
; R
my
–
сопротивления подводящих проводов между элемен-
тами измерительной схемы, учитываются при расчете автоматических по-
тенциометров высокой точности, например, класса 0,25.
Термопара или источник измеряемого напряжения постоянного тока
включены последовательно с электронным усилителем в одну из диагона-
лей измерительного моста. В другую диагональ включен источник стаби-
лизированного питания, обеспечивающий постоянство рабочего тока в из-
мерительной схеме.
При изменении сигнала Е
х
на входе усилителя возникает напряжение
разбаланса постоянного тока, которое преобразуется в напряжение пере-
менного тока и усиливается для приведения в действие реверсивного-
двигателя М. Вал двигателя связан с ползунком реохорда, указателем и пе-
ром. Действие компенсационной схемы сводится к автоматическому пере-
мещению ползунка по реохорду в сторону уменьшения напряжения рассо-
гласования (разности
ТЭДС
и падения напряжения на реохорде) до тех
пор, пока это напряжение не станет меньше зоны нечувствительности уси-
лителя. Таким образом, положение ползунка и, связанных с ним, указателя
и пера прибора однозначно определяет величины
ТЭДС
и, следовательно,
величину измеряемой температуры.
Расчет измерительной схемы автоматического потенциометра
1.
В соответствии с заданными пределами измеряемой температуры и
типом термопары по градуировочным таблицам определяем значение
ТЭДС
термопары, соответствующее верхнему E
max
и нижнему Е
min
значе-
нию пределов измерения температуры t
max
и t
min
. Значение предела измере-
ния Е
п
определяем как разность, т. е.
Е
п
= E
max
–
Е
min
.
29

2. Определяем величину R
с
из условия равенства падения напряжения
от тока I
2
на сопротивлении R
с
и
ЭДС
нормального элемента Е
с
:
R
с
I
2
= E
с
,
Е
с
принимаем равной 1,019 В.
В этом случае по нормальному элементу можно проверить работу ис-
точника стабилизированного питания. Задаваясь током верхней измери-
тельной ветви I
1
= 3 мА и нижней вспомогательной I
2
= 2 мА, получаем
2 · 10
‒3
R
с
= 1,019,
откуда R
с
= 509,5 Ом.
3.
Величину резистора R
pm
принимаем равной 750 Ом, переменного
резистора R′
pm
,
предназначенного для установки величины рабочего тока в
схеме, равной 56 Ом.
Определяем величину резистора предела измерения R
п
из условия, что
падение напряжения на цепи, состоящей из трех параллельно включенных
резисторов R
p
; R
ш
и R
п
, должно быть равно заданному пределу измерения
I
1
R
пр
= E
max
– E
min
,
откуда
1
п
пр
I
Е
R
=
.
(2.5)
Задаваясь эквивалентным сопротивлением реохорда R
экв
= 90, 100 и
300 Ом, получаем
ш
р
ш
р
экв
R
R
R
R
R
+
=
.
С учетом нерабочих участков реохорда R
пр
определяем выражением
k
R
R
R
R
R
⋅
+
=
)
(
о
экв
п
экв
пр
,
(2.6)
где
р
р
λ
λ
2
1
R
R
R
R
k
+
+
=
–
коэффициент, учитывающий нерабочие участки
реохорда;
р
λ
λ
0032
,
0
2
1
R
R
R
=
=
–
сопротивление нерабочих участков в ли-
30