Файл: Математические модели технических систем в расчетах на ЭВМ. Электрические цепи.pdf

11 

вектор,  изображающий  комплексное  число.  Этот  вектор  представляет со-
бой  амплитуду  некоторой  величины  (напряжение  или  ток),  которая  изме-
няется во времени по синусоидальному закону [1]. 

Здесь комплексное число равно  
 

1

2

j

A

Ae

A

jA









, 

(

2.1) 

где   А – модуль, равный длине вектора;  

φ  –угол  поворота  вектора А  относительно  оси  вещественных  значе-
ний (ось «+1»); 
А

1

  – вещественная  (действительная)  часть  комплексного  числа,  рав-

ная 

1

cos

A

A





; 

А

2

 – мнимая часть комплексного числа, равная 

2

sin

A

A





. 

Модуль А и угол φ определяются по формулам  
 

2

2

1

2

2

1

;

.

A

A

A

A

arctg

A









(2.2) 

 
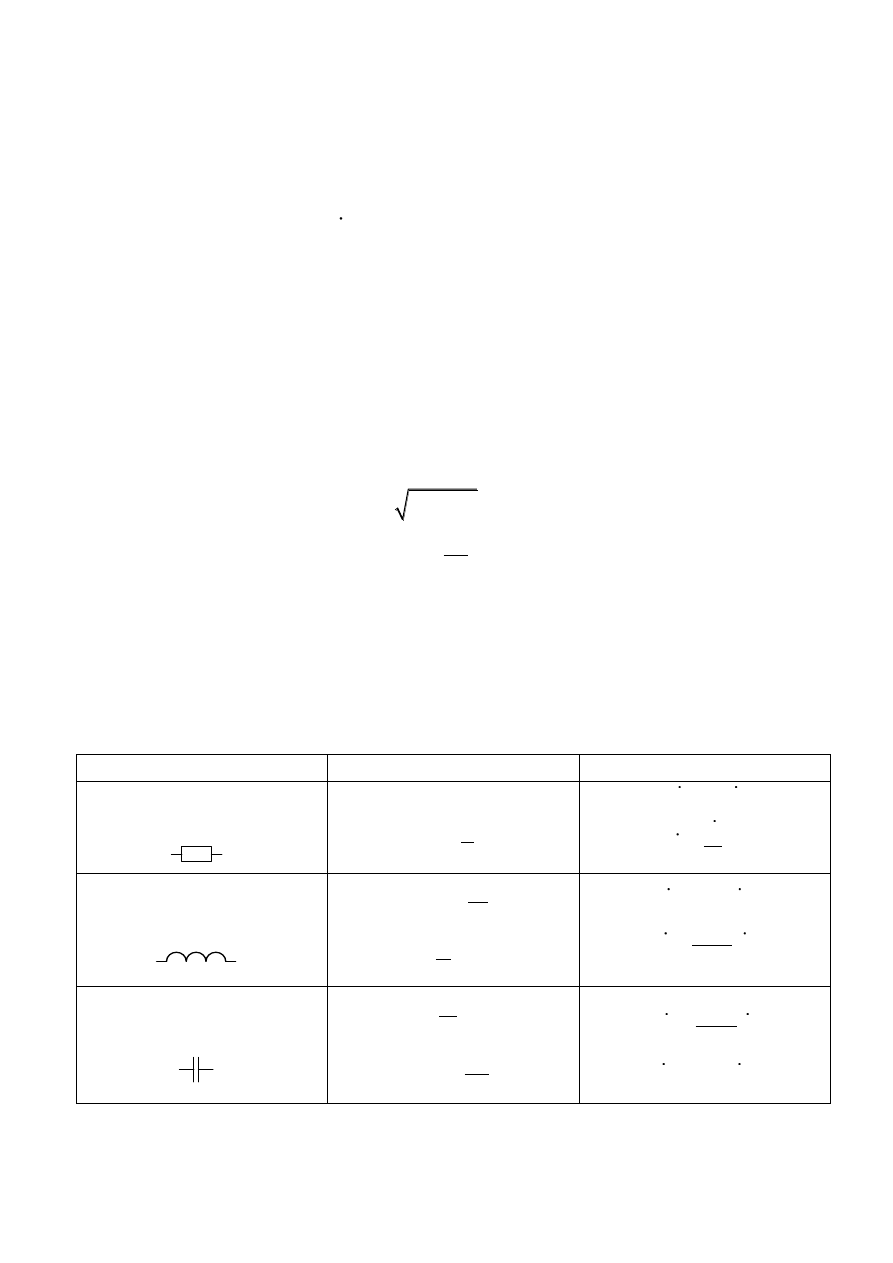
Примеры формы записи уравнений для различных типов сопротивле-

ний приведены в табл. 2.1. 

Таблица 2.1 

Формы записи уравнений на различных видах сопротивлений 

Вид сопротивления 

Общая форма записи 

Комплексная форма записи 

Активное 

R 

u

r i

u

i

r

 



U

r I

U

I

r

 



Индуктивное 

L 

1

di

u

L

dt

i

u dt

L







1

U

j LI

I

U

j L









Ёмкостное 

C 

1

u

i dt

C

du

i

C

dt







1

U

I

j С

I

j CU









 12 

В  работе  сначала  следует  построить  осциллограмму  тока  в  схеме  и 

напряжения источника ЭДС. Для этого необходимо определить  их ампли-
туду  I

амп

,  E

амп

и  угол  фазового  сдвига между током  и  напряжением  φ.  Для 

получения  амплитуды  искомой  величины  необходимо  действующее  зна-
чение этой величины умножить на 

2

. 

Изначально  создается  уравнение  равновесия  для  всей  схемы.  Для 

примера, показанного на рисунке 2.1, это уравнение  в общей форме запи-
сывается следующим образом:  

1

1

1

1

.

di

e

iR

i

idt

L

С

dt









(

2.3) 

 
Далее это уравнение необходимо записать в комплексной форме: 
 

1

1

1

;

E

IR

I

j LI

j С











(

2.4) 

 
или 
 

,

E

IZ



(

2.5) 

где  E – действующее значение напряжения источника ЭДС,  E =100 В;  

ω  –  угловая  частота  переменного  напряжения.  В  рассматриваемой 

работе частота переменного напряжения принимается равной f =50 Гц, по-
этому 

2

314,16

f









рад/с; 

Z

– общее сопротивление цепи,  

1

1

1

.

Z

R

j L

j С











(

2.6) 

Таким  образом,  действующее  значение  протекающего  в  схеме  тока 

составляет 

.

E

I

Z



(

2.7) 

 
При  решении  уравнения  (2.7)  получается  действующее  значение  ве-

личины тока в комплексной форме. Из этой величины с помощью уравне-
ний (2.2) определяется его амплитуда I

амп

и угол сдвига φ, которые необхо-

13 

димы для построения осциллограммы тока, протекающего в схеме. 

Далее следует построить осциллограммы напряжения на каждом эле-

менте  (сопротивлении).  Для  этого  необходимо  определить  их  амплитуды 
(U

амп1

, U

амп2

и U

амп3

) и углы сдвига (φ

1

, 

φ

2

и φ

3

). Определяются амплитуды и 

углы сдвига с помощью уравнений напряжения каждого элемента: 

1

1

1

1

1

1

;

1

;

.

R

C

L

U

IR

U

I

j C

U

j L I











(2.8) 

 
Из  полученных  значений  с  помощью  уравнений  (2.2)  определяются 

искомые амплитуды и углы фазового сдвига. 

Далее  необходимо  перевести  составленные  уравнения  в  программу 

Maple. 

Для мнимой единицы 

1



в Maple используется константа I. Зада-

ние комплексного числа не отличается от его обычного задания в матема-
тике. Для перехода от комплексной формы в тригонометрическую исполь-
зуются  операторы  Re  и  Im.  Оператор  Re  выделяет  из комплексного  числа 
вещественную часть, а оператор Im – мнимую.  

Программа  расчета  искомых  осциллограмм  для  заданной схемы  (ри-

сунок 2.1) приведена в приложении 2.  

Если  программа  составлена  правильно,  то  должны  построиться  два 

рисунка (осциллограммы). На первом рисунке изображена осциллограмма 
напряжения источника  ЭДС и тока, протекающего по цепи. На втором ри-
сунке изображены четыре осциллограммы напряжений: напряжение на ка-
ждом из трех сопротивлений схемы и сумма этих напряжений (входное на-
пряжения цепи). При этом на мониторе компьютера напряжение на первом 
элементе будет обозначено зеленой линией, на втором элементе – желтой 
линией,  на  третьем  элементе  –  синей  линией,  суммарное  напряжение  – 
красной  линией.  Осциллограмма  суммарного  напряжения  должна  полно-
стью совпадать с осциллограммой напряжения источника ЭДС.    

Оформление шага 

 
1. 

Записать исходные данные для расчета (только для студентов  заоч-

ной формы обучения), используя прил. 3, табл. 2. Студентам очной формы 
обучения задания выдает преподаватель. Выданные задания необходимо 
прикрепить к отчету. 

2. 

Записать уравнения, описывающие схему (формулы 2.3-2.8). 

4. Составить программу расчета цепи в программе Maple и произвести 

еѐ  расчет  (Приложение  2).  Рассчитанная  программа  должна  быть  пред-

 14 

ставлена в отчете. 

2.2 

Расчет цепи с помощью программы Multisim 

 
Для  расчета  заданной  схемы  в  программе  Multisim  необходимо  соз-

дать графическое представление схемы в рабочем окне программы. Как и 
в предыдущей работе, схема создается путем перетаскивания соответст-
вующих элементов схемы из библиотек в рабочее окно и последующего их 
соединения согласно заданной схеме. 

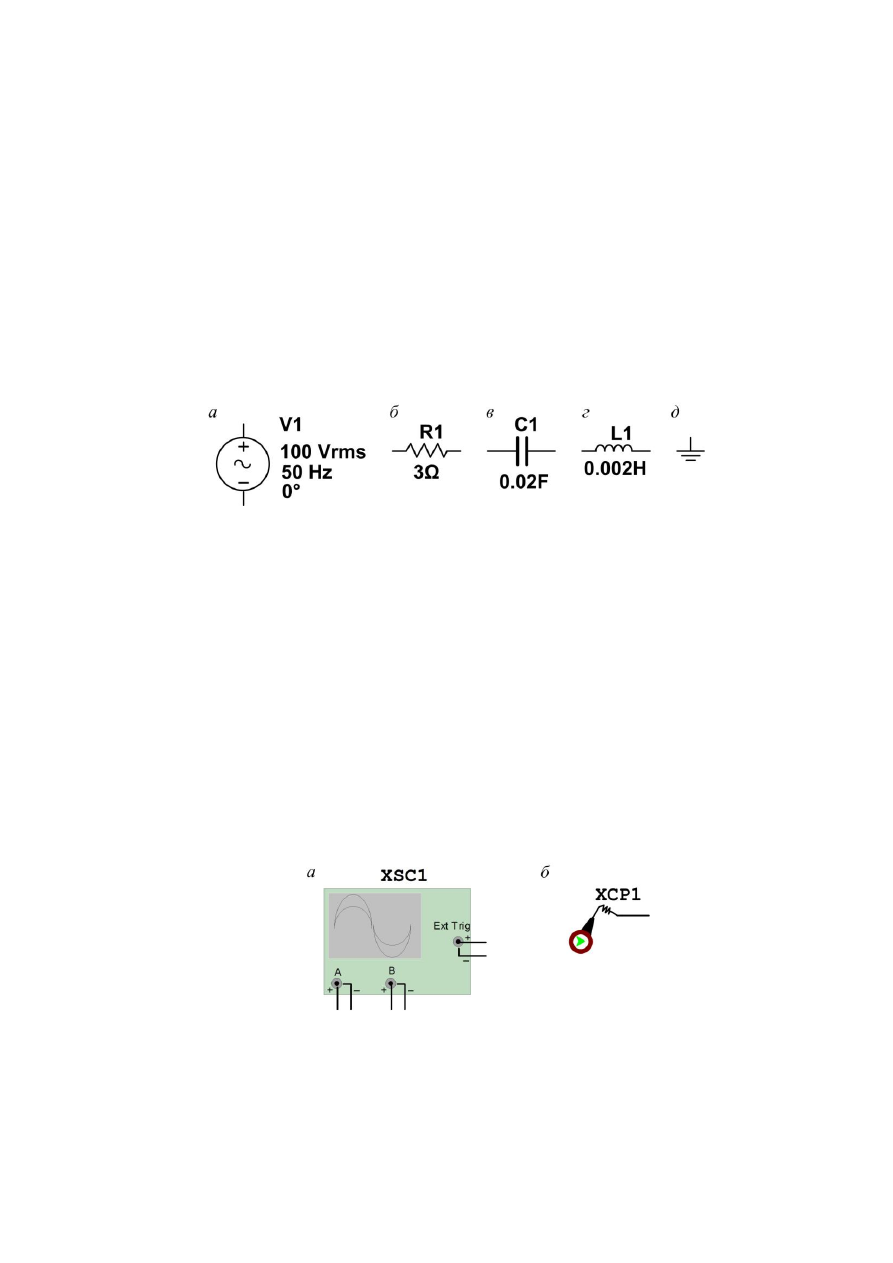
На  рис. 2.3  приведены  основные  компоненты,  необходимые  для  соз-

дания заданной схемы в программе  Multisim. Параметры каждого элемен-
та задаются в соответствующем окне, которое вызывается двойным щелч-
ком левой кнопкой мыши по элементу. 

Рис. 2.3. Основные компоненты, необходимые для создания заданной схемы:  

а – источник переменного напряжения (AC_POWER); б – резистор (RESISTOR);  

в – ѐмкость (CAPACITOR); г – индуктивность (INDUCTOR); д – заземление (GROUND) 

 
Элемент 

GROUND

необходим  для  установления  нулевого  потенциала 

на схеме. Такой элемент устанавливается в любом месте на схеме и толь-
ко один раз. 

Для построения осциллограмм тока и напряжения в заданной цепи ис-

пользуется элемент Oscilloscope (осциллограф), показанный на рис. 2.4, а. 
Для  определения  величины  тока,  протекающего  в  схеме,  используется 
элемент  Current Probe (датчик тока),  показанный на  рис. 2.4, б. Элементы 
Oscilloscope 

и  Current  Probe находятся на  панели инструментов в  правой 

части рабочего окна программы.   

Рис. 2.4. Элементы Oscilloscope (а) и Current Probe (б) 

Элемент Oscilloscope обладает двумя входными каналами (A и B), ка-

ждый  из  которых  имеет  положительный  и  отрицательный  контакты.  Для 

15 

определения  напряжения  на  желаемом  элементе  схемы  необходимо  со-
единить  эти  контакты  с  соответствующими  точками  на  схеме.  В  парамет-
рах осциллографа в графе scale каждого входного канала необходимо ус-
тановить «50 V/Div». 

При  измерении  тока  с  помощью  элемента  Current  Probe  необходимо 

выход  этого  элемента  соединить  с  положительным  контактом  любого 
входного канала осциллографа. В параметрах элемента необходимо уста-
новить соотношение измеряемой величины «1 mV/mA».  

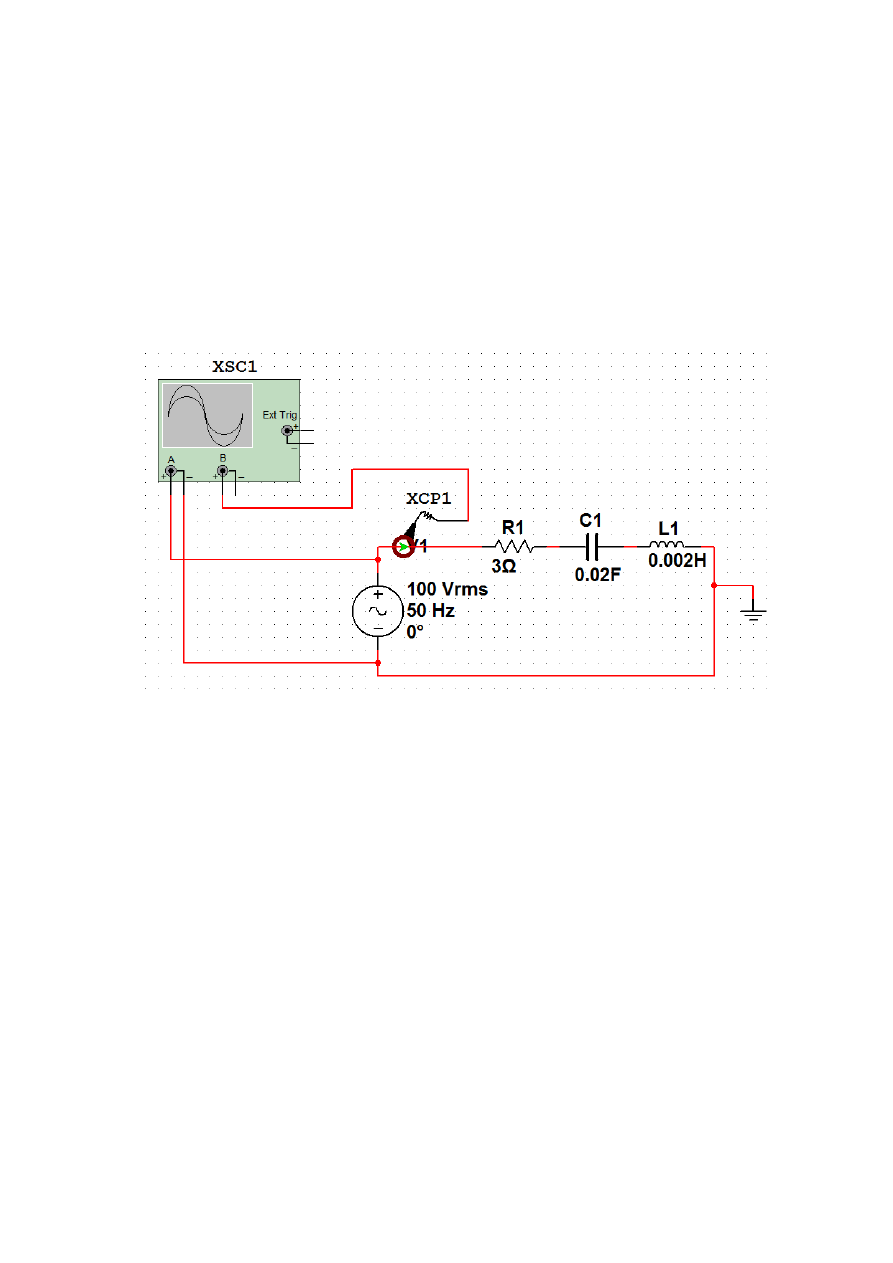
Внешний вид заданной схемы (рисунок 2.1) с подключенным осцилло-

графом, выполненной в программе Multisim представлен на рис. 2.5. 

Рис. 2.5. Внешний вид заданной схемы с подключенным осциллографом  

Для получения значений токов необходимо запустить моделирование 

путем нажатия клавиши  F5. Достаточно производить моделирование схе-
мы  в  течение  нескольких  секунд,  после  чего  необходимо  остановить  мо-
делирование  нажатием  клавиши  F6.  Полученные  осциллограммы  наибо-
лее удобно просматривать с помощью самописца, вызываемого командой 
«View/Grapher».  

Осциллограммы  тока  и  напряжения  источника  ЭДС,  полученные  при 

моделировании схемы (рис. 2.5), показаны на рис. 2.6. На полученных ос-
циллограммах  можно  изменить  цвет  фона  с  помощью  команды 
«Graph/Black and White  Colors».  Толщину  линий  можно  изменять  в  меню, 
которое вызывается двойным нажатием левой кнопкой мыши по соответ-
ствующей линии.