ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 07.11.2023
Просмотров: 48
Скачиваний: 2
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Асимметричные криптосистемы
Асимметричные методы используют два взаимосвязанных ключа: для шифрования и расшифрования. Один ключ является закрытым и известным только получателю. Его используют для расшифрования. Второй из ключей является открытым, т.е. он может быть общедоступным по сети и опубликован вместе с адресом пользователя. Его используют для выполнения шифрования.
Формально асимметричный метод можно описать следующим образом. Обозначим результат шифрования текста T с помощью открытого ключа - E(T), а результат расшифровки текста с помощью закрытого ключа - D(T). Тогда асимметричный метод должен отвечать следующим трем требованиям:
-
D(E(T)) = T; -
D практически невозможно определить по E; -
Е нельзя взломать.
Преимущество указанного метода состоит в уменьшении количества ключей, с которыми приходится оперировать. Однако данный алгоритм имеет существенный недостаток - требует значительной вычислительной мощности. Использование асимметричного метода шифрования представлено на Рис..
В настоящее время наиболее известными и надежными являются следующие асимметричные алгоритмы:
-
алгоритм RSA (Rivest, Shamir, Adleman); -
алгоритм Эль Гамаля.
Алгоритм RSA принят в качестве следующих международных стандартов: ISO/IEC/DIS 9594-8 и X.509. Алгоритм использует факт, что нахождение больших (например, 100-битных) простых чисел в вычислительном отношении осуществляется легко, однако разложение на множители произведения двух таких чисел в вычислительном отношении представляется невыполнимым.
Другим известным методом является алгоритм Эль Гамаля, положенный в основу стандарта NIST (NationalInstituteofStandardsandTechnology) - MD 20899. Алгоритм основан на возведении в степень по модулю большого простого числа.
Следует сказать, что, если алгоритмы типа DES определяют длину данных и ключа в битах, то асимметричные алгоритмы могут быть реализованы при любой длине ключа. Чем ключ длиннее, тем выше криптостойкость системы, но больше время шифрования и расшифровывания.
Зашифрованный текст
Е(Т)
Текст
D(Е(Т))
Текст
Т
Шифратор
Дешифратор



Несекретный ключЕ
Секретный ключ D

Генератор ключей {E}, {D}
Рис. 2.2. Использование асимметричного метода шифрования с открытым ключом
Как отмечалось, основным недостатком асимметричных алгоритмов является их низкое быстродействие: данные алгоритмы в несколько тысяч раз медленнее симметричных алгоритмов! Поэтому для исключения данного недостатка используют технологии сочетания симметричных и асимметричных методов шифрования. В частности, текст шифруется быстродействующим симметричным алгоритмом, а секретный (случайный) ключ, сопровождающий текст, - асимметричным алгоритмом.
Рассмотрим более подробно алгоритм RSA
Функционирование криптосистемы на основе метода RSA предполагает формирование открытого и секретного ключей. С этой целью необходимо выполнить следующие математические операции:
-
Выбираем два больших простых числа р и q, понимая под простыми числами такие числа, которые делятся на само себя и число 1 -
Определяем n = pq, (произведение pиq) -
Вычисляем число k = (p-1) (q –1), -
Выбираем большое случайное число е, взаимно простое с числом k (взаимно простое число — это число, которое не имеет ни одного общего делителя, кроме числа 1) -
Определяем число d, для которого истинным является соотношение
(e х d) mod k = l, где mod–операция вычисления остатка от деления, например
5 mod 2 =1или 5 mod 5 = 0. -
Принимаем в качестве открытого ключа пару чисел {е, n} -
Формирование секретного ключа в виде пары чисел {d, n}
Для зашифровки передаваемых данных с помощью открытого ключа {е, n} необходимо выполнить операции:
-
Разбить шифруемый текст на блоки, каждый из которых может быть представлен в виде последовательности чисел M(i), где i= 0,1,..., n –1
Если шифруется текстовое сообщение, то самый простой способ разбить сообщение на текстовые блоки по nсимволов, затем представитькаждый текстовый блок в виде последовательности чисел - порядковых номер символов в используемом алфавите
-
Зашифровать текст в виде последовательности чисел M(i) по формуле
C(i) = (M(i)e) modn
Расшифрованиешифротекста производится с помощью секретного ключа {d, n} при выполнении следующих вычислений: M(i) = (C(i)d) modn
В результате получаем последовательность чисел M(i), представляющих исходные данные. На практике при использовании метода RSA длина р и q составляет 100 и более десятичных знаков, что обеспечивает высокую криптостойкостьшифротекста.
Следующий пример наглядно демонстрирует алгоритм шифрования RSA:
Зашифруем и расшифруем сообщение "САВ" по алгоритму RSA. Для простоты возьмем небольшие числа - это сократит наши расчеты.
Выберем p=3 and q=11.
Определим n= 3*11=33.
Hайдемk=(p-1)(q-1)=2*10=20. Следовательно, d будет равно, например, 3: (d=3), поскольку числа k=20 и d=3 –взаимно простые.
Выберем число е по следующей формуле: (e*3) mod 20=1. Значит е будет равно, например, 7: (e=7), поскольку (7*3) mod 20 = 21 mod 20 = 1(остаток от деления 21 на 20 равен 1).
Представим шифруемое сообщение как последовательность чисел в диапозоне от 0 до 32 (незабывайте, что кончается на n-1=32). Сформируем последовательность M(i), заменяя символы на их порядковые номера в алфавите (буква А↔1, буква В↔2, буква С↔3): M(1)=3, M(2)=1,M(3)=2.
Порядок букв в алфавите определяем при шифровке и расшифровке по одной и той же таблице, например:
| Номер | Символ | Номер | Символ | Номер | Символ |
| 0 | ‘ | 11 | K k | 22 | V v |
| 1 | A a | 12 | L l | 23 | W w |
| 2 | B b | 13 | M m | 24 | X x |
| 3 | C c | 14 | N n | 25 | Y y |
| 4 | D d | 15 | O o | 26 | Z z |
| 5 | E e | 16 | P p | 27 | . |
| 6 | F f | 17 | Q q | 28 | , |
| 7 | G g | 18 | R r | 29 | ! |
| 8 | H h | 19 | S s | 30 | ? |
| 9 | I i | 20 | T t | 31 | пробел |
| 10 | J j | 21 | U u | 32 | дефис |
| | | | | | |
Теперь зашифруем сообщение, используя открытый ключ {7,33}
C(1) = M(1)e mod n = 37 mod 33 = 2187 mod 33 = 9;
C(2) = M(2)e mod n= 17 mod 33 = 1 mod 33 = 1;
C(3) = M(3)e mod n= 27 mod 33 = 128 mod 33 = 29;
Получили следующее сообщение: IA!
Теперь расшифруем данные, используя закрытый ключ {3,33}.
M(1)=(C(1)d) mod n = 93 mod 33 =729 mod 33 = 3(С);
M(2)= (C(2)d) mod n = 13 mod 33 =1 mod 33 = 1(А);
M(3)=(C(3)d) mod n = 293 mod 33 = 24389 mod 33 = 2(В);
Получили исходное сообщение: CAB.
Данные расшифрованы!
Электронная цифровая подпись
Электронная цифровая подпись (ЭЦП) — реквизит электронного документа, полученный в результате криптографического преобразования информации с использованием закрытого ключа подписи и позволяющий проверить отсутствие искажения информации в электронном документе с момента формирования подписи (целостность), принадлежность подписи владельцу сертификата ключа подписи (авторство), а в случае успешной проверки подтвердить факт подписания электронного документа (неотказуемость).
Электронная подпись предназначена для определения лица, подписавшего электронный документ, и является аналогом собственноручной подписи в случаях, предусмотренных законом.
Электронная подпись применяется при совершении гражданско-правовых сделок, оказании государственных и муниципальных услуг, исполнении государственных и муниципальных функций, при совершении иных юридически значимых действий.
Использование ЭЦП предполагается для осуществления следующих важных направлений в электронной экономике:
-
Полный контроль целостности передаваемого электронного платежного документа: в случае любого случайного или преднамеренного изменения документа цифровая подпись станет недействительной, потому как вычисляется она по специальному алгоритму на основании исходного состояния документа и соответствует лишь ему. -
Эффективная защита от изменений (подделки) документа. ЭЦП даёт гарантию, что при осуществлении контроля целостности будут выявлены всякого рода подделки. Как следствие, подделывание документов становится нецелесообразным в большинстве случаев. -
Фиксирование невозможности отказа от авторства данного документа. Это аспект вытекает из того, что вновь создать правильную электронную подпись можно лишь в случае обладания так называемым закрытым ключом, который, в свою очередь, должен быть известен только владельцу этого самого ключа (автору документа). В этом случае владелец не сможет сформировать отказ от своей подписи, а значит — от документа. -
Формирование доказательств подтверждения авторства документа: исходя из того, что создать корректную электронную подпись можно, как указывалось выше, лишь зная Закрытый ключ, а он по определению должен быть известен только владельцу-автору документа, то владелец ключей может однозначно доказать своё авторство подписи под документом. Более того, в документе могут быть подписаны только отдельные поля документа, такие как «автор», «внесённые изменения», «метка времени» и т. д. То есть, может быть доказательно подтверждено авторство не на весь документ.
Идея технологии электронной подписи состоит в следующем. Отправитель передает два экземпляра одного сообщения: открытое и расшифрованное его закрытым ключом (т.е. обратно шифрованное). Получатель шифрует с помощью открытого ключа отправителя расшифрованный экземпляр. Если он совпадет с открытым вариантом, то личность и подпись отправителя считается установленной.
Формально выражаясь, асимметричный метод обеспечивает реализацию электронной подписи при выполнении следующего тождества:
E(D(T)) = D(E(T)) = T.
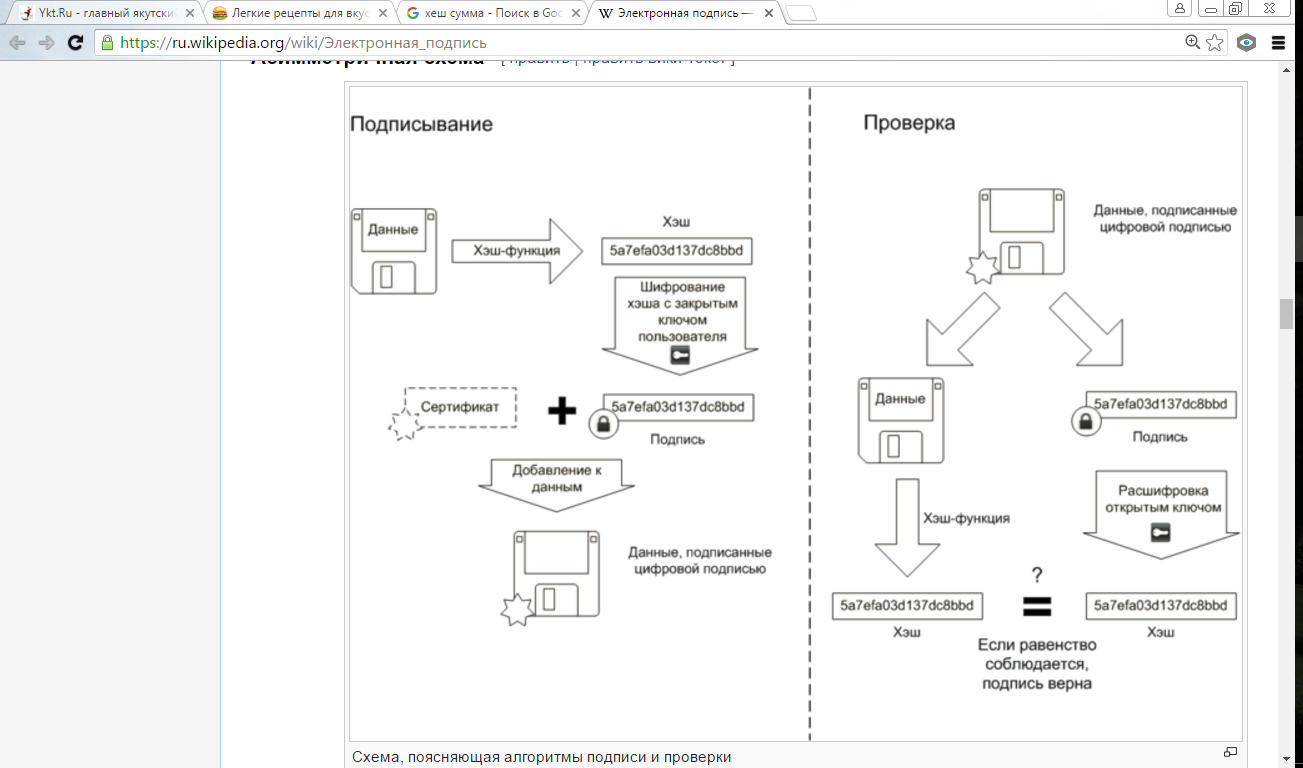
При практической реализации электронной подписи также шифруется не все сообщение, а лишь специальная контрольная сумма - хэш (hashtotal), защищающая послание от нелегального изменения. Важно, что электронная подпись здесь гарантирует как целостность сообщения, так и удостоверяет личность отправителя.
Асимметричные схемы ЭП относятся к криптосистемам с открытым ключом. В отличие от асимметричных алгоритмов шифрования, в которых шифрование производится с помощью открытого ключа, а расшифровка — с помощью закрытого, в асимметричных схемах цифровой подписи подписание производится с применением закрытого ключа, а проверка подписи — с применением открытого.
Общепризнанная схема цифровой подписи охватывает три процесса:
-
Генерация ключевой пары. При помощи алгоритма генерации ключа равновероятным образом из набора возможных закрытых ключей выбирается закрытый ключ, вычисляется соответствующий ему открытый ключ. -
Формирование подписи. Для заданного электронного документа с помощью закрытого ключа вычисляется подпись. -
Проверка (верификация) подписи. Для данных документа и подписи с помощью открытого ключа определяется действительность подписи.
Закрытый ключ является наиболее уязвимым компонентом всей криптосистемы цифровой подписи. Злоумышленник, укравший закрытый ключ пользователя, может создать действительную цифровую подпись любого электронного документа от лица этого пользователя. Поэтому особое внимание нужно уделять способу хранения закрытого ключа. Пользователь может хранить закрытый ключ на своем персональном компьютере, защитив его с помощью пароля. Однако такой способ хранения имеет ряд недостатков, в частности, защищённость ключа полностью зависит от защищённости компьютера, и пользователь может подписывать документы только на этом компьютере.