Файл: Информационные технологии-Багиева.docx

Глава 1. Планирование эксперимента

Содержательный анализ проблем моделирования, определяемых соотношением между реальным экспериментом, модельным экспериментом и теорией, свидетельствует о постоянном внимании исследователей к поиску возможных стратегий моделирования с учетом особенностей исходной информации. Развитие этих подходов связано с применением интеллектуальные системы (ИС) и стремительно растущей производительности вычислительных средств.

Глава 2. Формальные процедуры

Формальные процедуры, лежащие в основе функционирования ИС, предполагают широкое использование измерительной информации и методов математического моделирования. Решение прикладных задач анализа и прогноза поведения динамического объекта в ИС ведется статистическими методами с привлечением теории планирования эксперимента.

Особенности планирования эксперимента

Возникающие при практическом использовании ИС задачи планирования эксперимента часто выходят за рамки классического подхода и требуют специального обобщения с учетом особенностей рассматриваемых проблем. В реальных измерениях ресурсы могут быть существенно ограничены, а априорная информация недостаточна для несмещенной оценки функции регрессии. В этих условиях приходится считаться не только со случайной ошибкой приближения, но и с систематической ошибкой, вызванной неадекватностью принятой модели. Выбор пространства, в котором ищется оценка, приходится осуществлять совместно с планом эксперимента и методом оценивания.

Таблица 1.Характеристика метода оценивания

Выбор оптимальных условий эксперимента

Задача выбора оптимальных условий эксперимента в ИС определяет надежную оценку характеристик динамического объекта и параметров внешней среды и связана с построением нормированного дискретного плана для динамического объекта, развивающегося во времени и пространстве. Пассивная стратегия планирования такого эксперимента характеризуется тем, что объект функционирует в режиме нормальной эксплуатации. ИС на основе анализа ситуации выбирает моменты времени и координаты точек, в которых следует производить измерения.

Глава 3. Оптимальная структура моделей

В условиях эксплуатации ИС функционируют в реальном масштабе времени, и значительное усложнение используемых математических моделей приводит к громоздким алгоритмам преобразования измерительной информации, затрудняющим процедуру адаптации на выделенном временном интервале.

Таблица 2.Эксперимент 1 - полная адекватная модель; 2 - модель с недобором; 3 - модель с перебором

Планирование измерительного эксперимента в ИС реального времени связано с выбором оптимальных условий измерений, обеспечивающих надежную оценку характеристик динамического объекта и параметров внешней среды и с организацией процедурной компоненты базы знаний ИС и соответствующего алгоритмического и программного обеспечения.

Задание 2. (Наберите текст с использованием заголовков различных уровней, названий схем. В конце документа создайте оглавление, список иллюстраций и предметный указатель для слов выделенных курсивом)

ВВЕДЕНИЕ

Развитие новых технологий и широкое внедрение математических методов в экономические исследования, а также рост числа выпускаемой вычислительной техники и повышение её качества привели к широкому использованию ПЭВМ во многих областях народного хозяйства.

Для этих целей существуют не только мощные и удобные универсальные ПЭВМ, но и хорошо разработанный арсенал численных методов.

Глава 1. Аппроксимация функций

Аппроксимацияиспользуется для случая, когда значения функцииf(x) определены только в узлах х_i, а значения функции в промежуточных точках не известны. В этом случае исходную функциюf(x) требуется приближенно заменить (аппроксимировать) некоторой функцией(х), так чтобы отклонение(х) отf(x) в заданной области было наименьшим.

Основные методы аппроксимации функции: интерполирование и подбор эмпирических формул (схема 1).

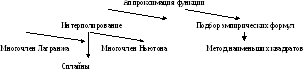
Схема 1.Аппроксимация функций

Глава 2. Методы оптимизации

Оптимизация как раздел математики существует достаточно давно. Оптимизация - это выбор, т.е. то, чем постоянно приходится заниматься в повседневной жизни. Термином "оптимизация" в литературе обозначают процесс или последовательность операций, позволяющих получить уточненное решение. Хотя конечной целью оптимизации является отыскание наилучшего или "оптимального" решения, обычно приходится довольствоваться улучшением известных решений, а не доведением их до совершенства. По этому под оптимизацией понимают скорее стремление к совершенству, которое, возможно, и не будет достигнуто.

Одномерная оптимизация

Одномерная задача оптимизации в общем случае формулируется следующим образом. Найти наименьшее (или наибольшее) значение целевой функцииу = f (х),заданной на множествеа,и определить значение проектного параметрах Єσ, при котором целевая функция принимает экстремальное значение (схема 2).

Схема 2.Методы одномерной оптимизации

Многомерные задачи оптимизации

Постановка задачи оптимизации включает в себя множество допустимых решений X ={x₁, x₂, … x_n} и числовую функцию f, определенную на этом множестве, которая называется целевой функцией. Для решения многомерных задач оптимизации используются методы: покоординатного и градиентного спуска.