Файл: Методичка Excel.docx

Таблица 4.2

Аргументы финансовых функций Excel анализа ценных бумаг

Примечания:

1. Аргумент Частота (Периодичность) задается как число, принимающее следующие значения в зависимости от количества выплат по купонам за год:

• один раз в год (ежегодная выплата);

• два раза в год (полугодовая выплата);

• четыре раза в год (ежеквартальная выплата).

2. Аргумент Базис не является обязательным, однако играет важную роль, поскольку влияет на точность вычислений. В зависимости от способа вычисления временного периода аргумент Базис может принимать следующие значения:

1. -US(NASD) — американский стандарт, месяц равен 30, а год — 360 дням; принимается по умолчанию;

2. - фактический/фактический — фактическая длина месяца и года;

3. - фактический/360 — фактическая длина месяца, год равен 360 дням;

4. - фактический/365 — фактическая длина месяца, год равен 365 дням;

5. -европейский 30/360 — европейский стандарт, длина месяца равна 30 дням, длина года принимается 360 дней.

Следует отметить, что все даты должны быть выражены в числовом формате.

4.2 Примеры решения задач

Пример 1. Рассмотрим возможность приобретения облигаций трех типов, каждая из которых с номиналом в 100 руб. и сроком погашения 09.10.2012. Курсовая стоимость этих облигаций на дату 25.07.2010 составила соответственно 90, 80 и 85 руб.

Годовая процентная ставка по купонам (размер купонных выплат) составляет:

для первой облигации — 8% при полугодовой периодичности выплат;

для второй облигации — 5% при ежеквартальной периодичности выплат;

для третьей облигации — 10% с выплатой один раз в год.

Расчеты ведутся в базисе фактический/фактический.

Необходимо провести анализ эффективности вложений в покупку этих облигаций, если требуемая норма доходности составляет 15%.

Решение. Чтобы оценить эффективность вложений в покупку каждой из облигаций, рассчитаем их годовую доходность, используя функцию ДОХОД:

Доход(дата_согл; дата_вступл_в_силу; ставка; цена; погашение; частота; базис)

Для решения задачи составим на листе Excel таблицу с исходными данными и формулами расчета требуемых величин (рис.4.1).

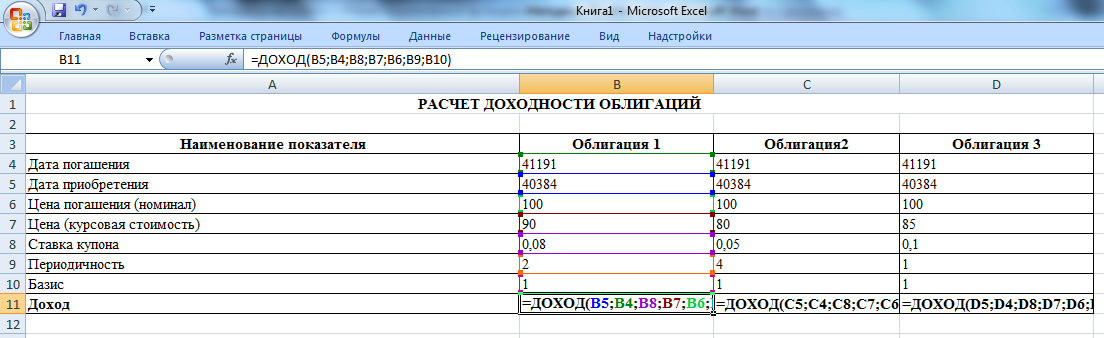
Рис. 4.1. Применение функции ДОХОД для оценки доходности облигаций (режим отображения формул)

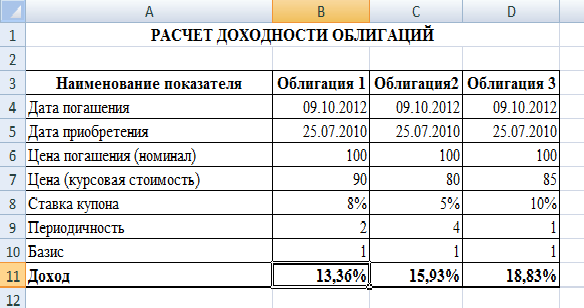
Рис. 4.2. Применение функции ДОХОД для оценки доходности облигаций

Примечание: в ячейках В11, С11, D11 (строка «доход») необходимо применить формат «процентный»).

Выполним также расчет доходности, непосредственно задавая значения аргументов в функции ДОХОД.

Аргументы, содержащие даты, введем с помощью функции ДАТА (можно также указывать ссылки на ячейки, содержащие даты).

Облигация первого типа:

=ДОХОД(ДАТА(2005;7;25);ДАТА(2007;10;9); 8%;90;100;2;1)=13,36%

Облигация второго типа:

=ДОХОД(ДАТА(2005;7;25);ДАТА(2007;10;9); 5%;80;10;4;1)=15,93%

Облигация третьего типа:

=ДОХОД(ДАТА(2005;7;25);ДАТА(2007;10;9); 10%;85;100;1;1)=18,83%

Результаты, полученные различными способами, совпадают.

Вывод: доходность по второй и третьей облигациям (15,93% и 18,83% соответственно) выше заданной нормы (15%), а по первой облигации (13,36%) — ниже. Следовательно, целесообразно покупать облигации второго и третьего типов.

Пример 2. Коммерческий банк предлагает свои сберегательные сертификаты номиналом 100 000 руб. сроком на восемь месяцев. Дата соглашения — 10.01.2012. Цена продажи составляет 85 000 руб. Способ вычисления дня — фактический/360. Необходимо определить доход за этот период.

Решение. Для вычисления доходности данной финансовой операции, возвращающейся в виде годовой ставки, рассчитанной по простым процентам, используем функцию ИНОРМА, которая задается следующим образом:

Инорма(дата_согл; дата_вступл_в_силу; инвестиция; погашение; базис)

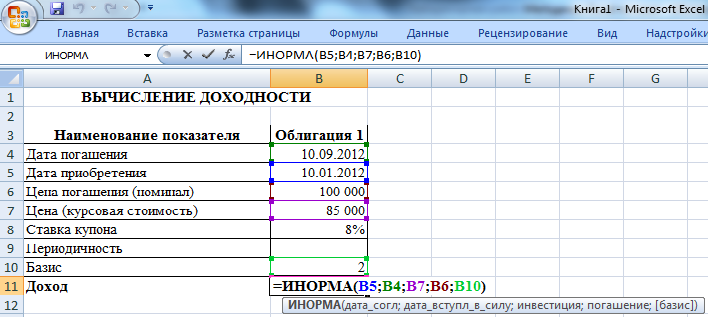
Рис. 4.3. Вычисление доходности сберегательного сертификата

Исходные данные задачи представим в виде таблицы. В соответствующую ячейку введем формулу, обеспечивающую вычисление доходности сберегательного сертификата (рис. 4.3).

Для проверки правильности результата в функцию ИНОРМА введем значения аргументов в непосредственном виде:

=ИНОРМА( ДАТА(2012;1;10);ДАТА(2012;9;10);85000;100000;2)=26,14%

Пример 3. Облигация номиналом в 10 000 руб. и сроком погашения 20.07.2012 приобретена 05.05.2010. Выплаты по купонам осуществляются каждые полгода при способе вычисления дня - фактический/365. Необходимо определить:

• количество предстоящих купонных выплат;

• дату предшествующей купонной выплаты;

• дату следующей купонной выплаты;

• длительность купонного периода;

• количество дней от начала действия периода до даты соглашения;

• количество дней от даты соглашения до даты следующего периода.

Решение: данная задача решается с применением специальных функций, предназначенных для определения различных технических характеристик купонов облигаций. К функциям данной группы относятся:

• ДНЕЙКУПОНДО(дата_согл; дата_вступление_в_силу; частота; базис);

• ДНЕЙКУПОН(дата_согл; дата_вступл_в_силу; частота; базис);

• ДНЕЙКУПОНПОСЛЕ(дата_согл; дата_вступл_в_силу; частота; базис);

• ДАТАКУПОНДО(дата_согл; дата_вступл_в_силу; частота; базис);

• ДАТАКУПОНПОСЛЕ(дата_согл; дата_вступл_в_силу; частота; базис);

• ЧИСЛКУПОН(дата_согл; дата_вступл_в_силу; частота; базис).

Исходные данные задачи введем в таблицу и рассчитаем требуемые показатели. После получения результатов для ячеек с датами зададим формат представления информации в виде даты (после вычислений получается числовой формат). Пример решения задачи показан на рис. 4.4

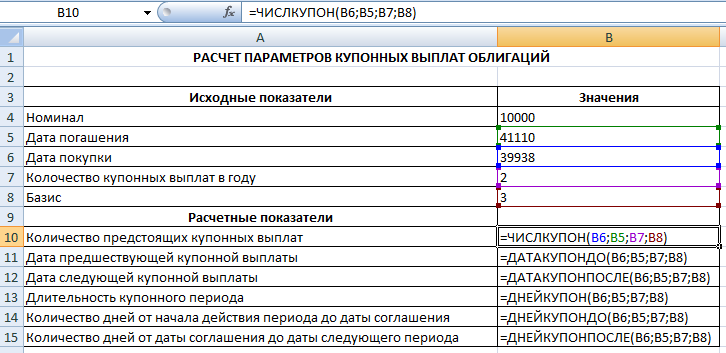
Рис. 4.4. Расчет параметров купонных выплат облигаций (режим отображения формул)

Результат вычислений представлен на рис. 4.5.

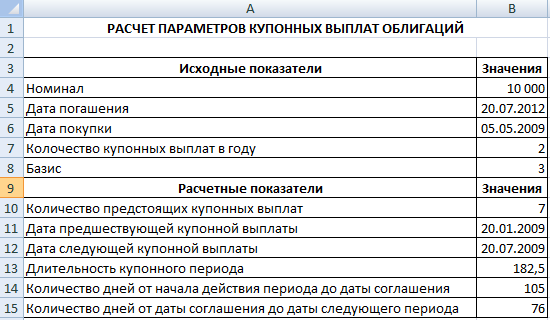
Рис.4.5. Результат вычисления параметров купонных выплат облигаций

Пример 4. Вексель выдан 12.07.2009 с датой погашения 25.12.2009. Цена векселя составляет 200 000 руб., а выкупная цена 250 000 руб. При расчетах используется базис фактический/фактический. Необходимо определить величину учетной ставки. Необходимо определить величину учетной ставки можно с помощью функции СКИДКА: