ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 22.05.2024
Просмотров: 210
Скачиваний: 0
СОДЕРЖАНИЕ
В. А. Четвергов, с. М. Овчаренко
1. Классификация процессов изменения свойств материалов
2. Классификация процессов изменения свойств работоспособности элементов
3. Закономерности физико-химических процессов
3.1. Общие закономерности процессов механического разрушения
3.2. Процессы механического разрушения металлов и сплавов
3.3. Процессы механического разрушения полимерных материалов
3.4. Механизм образования и развития трещин
3.5. Влияние характера изменения нагрузки на разрушение материалов
3.6. Адсорбционное понижение прочности под действием поверхностно-активных веществ
3.7. Процессы теплового разрушения твердых тел
4. Процессы электрического разрушения твердых диэлектриков и полупроводников
5.1. Старение материалов и сплавов
5.2. Старение, обусловленное распадом пересыщенных твердых растворов
5.3. Старение полимерных материалов
Большое практическое значение имеет знание закономерностей разрушения составных материалов, армированных волокнами. Механизм разрушения этих материалов представляется следующим. Вследствие того, что волокна имеют дефекты, распределенные по их длине, разрушение волокон происходит в некоторых случайных точках (сечениях) при нагрузках, меньших, чем общая разрушающая нагрузка для составного материала. В месте разрушения волокна возникает концентрация напряжений, которая при увеличении нагрузки может вызвать появление небольших местных трещин в связующем (основном) материале. В процессе дальнейшего нагружения за счет сдвига связующего материала смежные трещины соединяются друг с другом. Этот процесс разрыва во-
18
локон, возникновения местных трещин в основном материале и соединения смежных трещин продолжается непрерывно до общего разрушения составного материала.
3.4. Механизм образования и развития трещин
Локальный характер разрыва твердых тел показывает, что кинетика разрушения (и долговечность материала) определяется прежде всего развитием трещин разрушения. Механизм процесса разрушения при длительном воздействии нагрузки сводится к постепенному росту микротрещин до критического размера в результате флуктуационного разрыва атомных связей в вершине (устье) трещины. Таким образом, развитие микротрещин в напряженном теле представляет собой сущность процесса разрушения.
Исследования показывают, что трещины образуются вскоре после приложения нагрузки обычно на различного рода дефектах: включениях, неоднородностях, царапинах, и их развитие занимает основную часть времени до разрыва (например, в меди на развитие видимых трещин до разрыва затрачивается 90 % времени, в пластмассах–до 99 % ). Обычно различают две стадии роста трещины: стадию медленного роста с увеличивающейся скоростью (стадию ускоренного роста), преобладающую по времени, и стадию быстрого роста с постоянной предельной скоростью, близкой к скорости звука в материале. Длительность этой стадии составляет незначительную долю по сравнению с длительностью ускоренной стадии и временем разрыва образца.
Время до разрушения (долговечность под нагрузкой) определяется скоростью роста трещин на ускоренной стадии [1]
![]() при
при
![]() и
и![]() ;
(11)
;
(11)
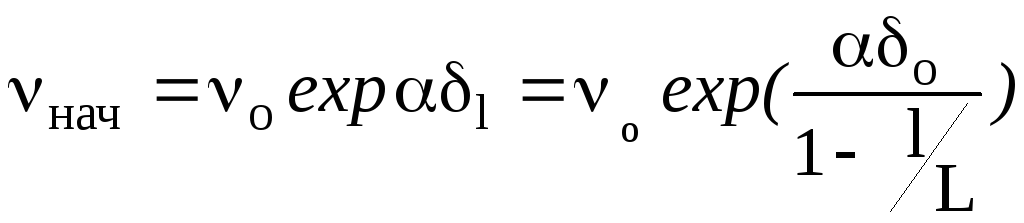 ,
(12)
,
(12)
где
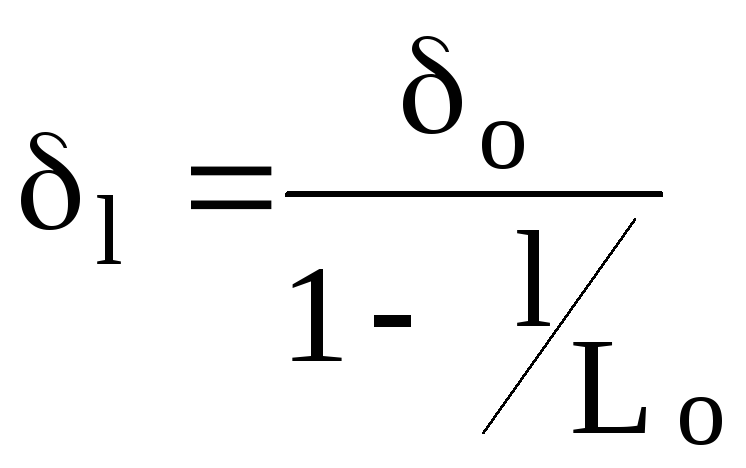
среднее напряжение в оставшейся
неразорванной части образца;
среднее напряжение в оставшейся
неразорванной части образца;
![]() среднее приложенное
напряжение;
среднее приложенное
напряжение;
L ширина образца;
l длина трещины;
19
![]()
относительная длина трещины;
относительная длина трещины;
и о постоянные, определяемые свойствами материала;
коэффициент, характеризующий самоускорение процесса разрыва при
данных значениях напряжения и температуры.
Экспоненциальная
связь между скоростью роста трещины и
напряжением определяет лавинообразный
характер развития трещин; увеличение
длины трещины под действием постоянной
нагрузки приводит к постепенному
увеличению напряжения
![]() ,
что, в свою очередь, согласно уравнению
(12) резко увеличивает скорость роста
трещины и вызывает самоускорение
процесса ее развития. Такой характер
зависимости скорости распространения
трещины объясняет, почему имеющиеся в
материале дефекты, создавая локальные
перенапряжения, тем самым становятся
центрами разрушения. Исследования
свидетельствуют об отсутствии порогового
напряжения для начала роста трещины.
,
что, в свою очередь, согласно уравнению
(12) резко увеличивает скорость роста
трещины и вызывает самоускорение
процесса ее развития. Такой характер
зависимости скорости распространения
трещины объясняет, почему имеющиеся в
материале дефекты, создавая локальные
перенапряжения, тем самым становятся
центрами разрушения. Исследования
свидетельствуют об отсутствии порогового
напряжения для начала роста трещины.
На основании
уравнений (11), (12), записанных в
дифференциальной форме
![]() ,
полагаем, что приt
= 0 длина трещины
,
полагаем, что приt
= 0 длина трещины
![]() ,
а по истечении времени
трещина пересечет весь образец, т. е.
,
а по истечении времени
трещина пересечет весь образец, т. е.
![]() .
(13)
.
(13)
Значения времени , необходимые для разрушения (разрыва) образца, вычисленные по скорости роста трещин (11), совпадают со значениями времени, полученными при эксперименте. В пределе при мгновенном приложении нагрузки, создающей среднее напряжение, равное теоретической прочности ( = теор), все связи в сечении будут разрываться одновременно и будет близко к 0.
Время до разрушения зависит от формы и размеров нагруженного образца (детали). Переход от одной формы образца к другой, хотя и не изменяет основных выводов, но меняет вид получаемых аналитических зависимостей.
3.5. Влияние характера изменения нагрузки на разрушение материалов
Процессы разрушения материалов сводятся, главным образом, к постепенному росту деформаций и трещин, к постепенному накоплению локальных дефектов, которое становится возможным вследствие необратимого характера
последовательных случайных единичных нарушений (необратимости каждого
20
парциального влияния нагрузки). Необратимость процесса накопления повреждений подтверждается результатами опытов с прерыванием нагрузки и последующим нагружением; при этом суммарное время пребывания под нагрузкой до разрушения в среднем равно долговечности образцов материала при непрерывном нагружении.
В случае изменяющегося во времени напряжения произвольной последовательности напряжений i, каждому из которых соответствует долговечность (i), причем время действия каждого напряжения равно ti разрыв образца произойдет тогда, когда сумма относительных уменьшений долговечности (располагаемого ресурса) станет равной единице. Для случая дискретной зависимости напряжений от времени t, когда напряжение в отдельных интервалах времени остается постоянным, изменяясь только при переходе от одного интервала к другому, условия разрушения образца будут такими:
![]() ;
(14)
;
(14)
если напряжение является непрерывной функцией времени (t) , условие разрыва образца имеет вид:
![]() ,
(15)
,
(15)
где tp время до разрушения образца;
(t) временной режим нагружения;
(t)=![]()
долговечность при данном напряжении.
долговечность при данном напряжении.
Условия (14), (15) характеризуют принцип наложения или суммирования парциальных разрушений; отдельные локальные разрушения суммируются вплоть до предельного состояния, когда трещина достигает критической величины и происходит разрушение образца.
Процессы разрушения при циклическом режиме нагружения, для которого давно установлена временная зависимость прочности, и при статическом нагружении обычно противопоставляются друг другу; предполагается, что закономерности разрушения при циклическом и статическом нагружении различны. Однако кинетическая теория разрушения твердых тел дает основание считать, что, хотя характер изменения внешней нагрузки оказывает влияние на процессы деформации и разрушения, существует определенная общность процессов разрушения независимо от условий нагружения; процессы разрушения обусловлены одинаковым механизмом.
Скорость нагружения существенно влияет на механизм разрушения твер-
21
дого тела. При медленном увеличении нагрузки происходит упругая деформа-
ция, затем – пластическое течение твердого тела и, наконец, – его разрыв. Медленное возрастание механического напряжения может сопровождаться протеканием вторичных процессов в твердых телах и соответствующими обратимыми и необратимыми изменениями свойств тела. При большой скорости нарастания механического напряжения обычно происходит хрупкое разрушение большинства материалов.