ВУЗ: Томский государственный университет систем управления и радиоэлектроники
Категория: Учебное пособие
Дисциплина: Дискретная математика
Добавлен: 28.11.2018
Просмотров: 6269
Скачиваний: 13

51
Рис. 6
1
1
1
Рис. 7
1
1
×
×
×
×
×
×
×
×
×
×
×
×
1
1
1
f
3
=
f
3
=
1
1
Находим минимальную КНФ. Инверсия функции f
3
приве-
дена на рис. 7. Согласно этой карте получаем:
3
.
f
ACD
AC B
=
+
+
По теореме де Моргана получаем минимальную КНФ:
3
(
)(
) .
f
A
C
D A C B
=
+ +
+
Минимизируем четвертую функцию (рис. 8).
f
4
= (6, 15); [1, 2, 5, 9, 10, 13].
4
.
f
ABD
ACD
=
+
Рис. 8
1
1
Рис. 9
1
1
×
×
×
×
×
×
×
×
×
×
×
×
1
1
f
4
=
f
4
=
1
1
1
1
Находим минимальную КНФ. Инверсия функции f
4
приве-
дена на рис. 9. Согласно этой карте:
4
.
f
AD
AD B
C
=
+
+ +
По теореме де Моргана получаем минимальную КНФ:
4
(
)(
)
.
f
A
D A
D BC
=
+
+
Минимизируем пятую функцию (рис. 10).
f
5
= (3, 7, 11, 14, 15);
[1, 2, 5, 9, 10, 13].
5
.
f
AC
D
=
+
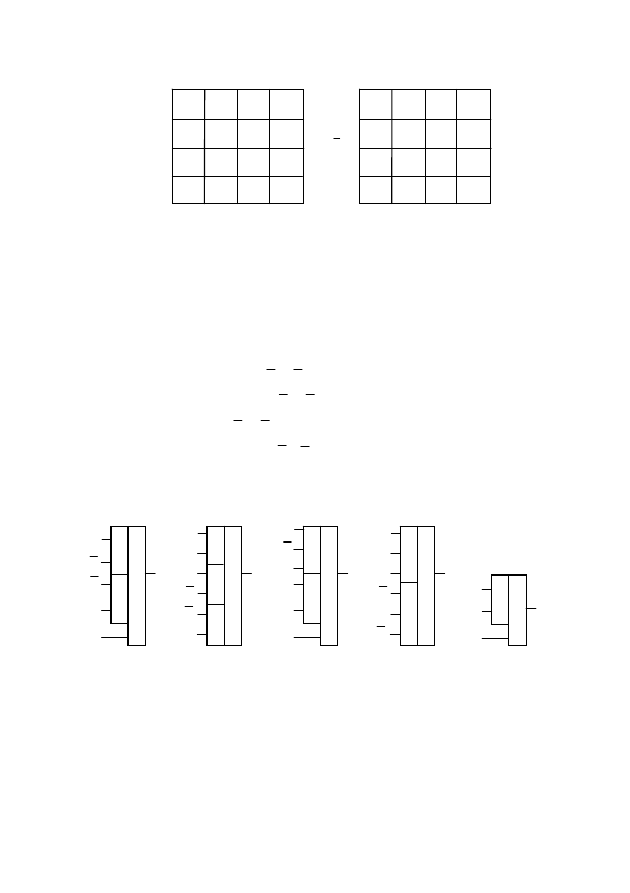
52
Рис. 10
1
1
Рис. 11
1
×
×
×
×
×
×
×
×
×
×
×
×
1
f
5
=
f
5
=
1
1
1
1
1
1
Находим минимальную КНФ (рис. 11):
5
(
) .
f
A
D C
=
+
Для построения преобразователя выбираем те функции, ко-
торые в аналитическом представлении имеют наименьшее число
букв. Если ДНФ и КНФ по числу букв одинаковы, то берем
ДНФ. В данном случае список булевых функций, имеет вид
1
.
f
D
AC
AB
= +
+
2
.
f
AD
BC
AB
=
+
+
3
(
)(
) .
f
A
C
D A C B
=
+ +
+
4
.
f
ABD
ACD
=
+
5
.
f
AC
D
=
+
Логическая схема преобразователя приведена на рис. 12.
A
С
A
B
D
&
&
1
f
1
A
С
A
C
B
&
1
f
3
1
D
A
B
D
A
D
&
&
1
f
4
C
A
D
B
C
B
&
&
1
f
2
A
&
A
C
D
& 1
f
5
Рис. 12
Оформление решения. Решение задачи на тему «Синтез
преобразователя кода» должно быть представлено в письменном
виде со следующим содержанием:
а) условие задачи, как оно сформулировано в задании;
б) таблица истинности. Составляется по аналогии с табли-
цей 1, приведенной выше в данном подразделе;

53
в) каждую булеву функцию представить в СДНФ (по образ-
цу, приведенному выше в данном подразделе);
г) минимальные ДНФ и КНФ для всех булевых функций;
д) карты Вейча для прямых и инверсных форм каждой из
пяти функций — всего 10 карт (по образцу, приведенному в
данном подразделе);
е) список пяти булевых функций, выбранных для построе-
ния логической схемы преобразователя и содержащих наи-
меньшее число вхождений переменных;
ж) логическая схема преобразователя (подобно рис. 12).
2.2 Тема 8: «Автомат на JK-триггерах»
Сначала рассмотрим некоторые исходные теоретические
положения, необходимые для синтеза автомата.
Триггер типа JK. Напомним основные сведения о триггере
типа JK. Триггер имеет синхронизирующий вход С (синхров-
ход) и два управляющих входа: J — единичный, K — нулевой
(рис. 13). Управление по этим входам осуществляется следую-
щим образом:
1) если J = K = 0, то триггер находится в
режиме хранения информации независимо от
того, поступают на его синхровход импульсы
тактового генератора или нет;
2) при J = 1, K = 0 синхроимпульс перево-
дит триггер в единичное состояние независимо
от того, в каком состоянии он находился до
подачи импульса;
3) если J = 0, K = 1, то синхроимпульс переводит триггер в
нуль независимо от предыдущего состояния;
4) при J = K = 1 триггер меняет состояние на противопо-
ложное с каждым синхроимпульсом.
Кроме того, JK-триггер имеет установочные входы R и S.
Эти входы используются в инициальных автоматах для уста-
новки их в исходное состояние. В процессе логического расчета
входы R и S не учитываются. Лишь после того как будет постро-
ен автомат (не являющийся инициальным), в нем необходимо
Рис. 13
Q
S
J
C
K
R
Q
ТТ

54
предусмотреть вход для его установки в исходное состояние.
Тогда автомат перейдет в разряд инициальных.
Многотактный автомат на JK-триггерах. В синхронных
многотактных автоматах импульсы, поступающие от генерато-
ра, подаются на синхровход каждого триггера, как показано на
рис. 14. Этот вход автомата условимся обозначать буквой φ.
В простейшем случае автомат реализует одну или несколь-
ко последовательностей своих внутренних состояний, где под
состоянием автомата понимается двоичное число, которое в
данный момент находится в
его внутренней памяти.
На рис. 14 внутренняя
память представлена регист-
ром, состоящим из триггеров
A, B, C,…, L. К их выходам
подключена комбинационная
схема, преобразующая со-
стояния регистра в код, по-
ступающий на управляющие
входы триггеров.
Задача синтеза много-
тактного автомата сводится к
разработке преобразователя
состояний автомата в выход-
ной код. Число выходов пре-
образователя в два раза
больше числа триггеров (так как JK-триггеры двухвходовые).
Строится преобразователь по очень простому принципу:
для каждого входного кода выходной код выбирается таким,
чтобы синхроимпульс переводил автомат в заранее заданное
состояние. Как выбирать эти выходные коды, показано на сле-
дующем примере.
Абстрактный синтез автоматов на JK-триггерах. Здесь и
далее показан образец решения задачи на тему «Синтез автома-
та на JK-триггерах» из второй контрольной работы Логические
условия для разработки автомата формулируются следующим
образом:
С
K
J ТТ
А
А
С
K
J ТТ
B
B
С
K
J ТТ
L
L
ϕ
J
A
…
…
Рис. 14
К
ом
бин
ац
ио
нн
ая
сх
ем
а K
A
J
B
K
B
J
L
K
L

55
Построить автомат на JK-триггерах, реализующий две по-
следовательности:
если A = 0, то 0, 2, 5, 6, 4, 1, 3, 7;
если A = 1, то 1, 6, 4, 7, 2, 3, 0, 5,
где десятичные цифры обозначают состояния автомата. Обе по-
следовательности являются циклически замкнутыми. Это зна-
чит, что при A = 0 после очередного тактового импульса автомат
из состояния 7 переходит в состояние 0, а при A = 1 после со-
стояния 5 автомат переходит в состояние 1 (также под действи-
ем синхроимпульса).
Исходным является нулевое состояние, т.е. 000.
Всего в каждой последовательности 8 состояний, следова-
тельно, для автомата необходимо предусмотреть три триггера. А
так как последовательностей две, то необходимо добавить еще
один триггер. Таким образом, для построения автомата, реали-
зующего две последовательности, необходимо четыре триггера.
Обозначим триггеры автомата буквами A, B, C, D. Триггеру
A отведем роль переключателя последовательностей с одной на
другую в соответствии с заданным условием.
Строим таблицу пере-
ходов состояний автомата
(табл. 2). Последовательно-
сти состояний, представ-
ленных в двоичных кодах,
указаны в колонках B, C, D.
Таблица по горизонта-
ли разделена линией на две
равные части, отделяющие
один цикл от другого. В
первой части, где A = 0, в
колонках B, C, D приведена
первая замкнутая последо-
вательность
трехзначных
двоичных кодов. Во второй
части — вторая последова-
тельность, также замкнутая
в своем цикле.
А B C D J
B
K
B
J
C
K
C
J
D
K
D
0 0 0 0 0 0
× 1 × 0 ×
2 0 0 1 0 1
× × 1 1 ×
5 0 1 0 1
× 0 1 × × 1
6 0 1 1 0
× 0 × 1 0 ×
4 0 1 0 0
× 1 0 × 1 ×
1 0 0 0 1 0
× 1 × × 0
3 0 0 1 1 1
× × 0 × 0
7 0 1 1 1
× 1 × 1 × 1
9 1 0 0 1 1
× 1 × × 1
14 1 1 1 0
× 0 × 1 0 ×
12 1 1 0 0
× 0 1 × 1 ×
15 1 1 1 1
× 1 × 0 × 1
10 1 0 1 0 0
× × 0 1 ×
11 1 0 1 1 0
× × 1 × 1
8 1 0 0 0 1
× 0 × 1 ×
13 1 1 0 1
× 1 0 × × 0
Таблица 2