ВУЗ: Томский государственный университет систем управления и радиоэлектроники
Категория: Учебное пособие
Дисциплина: Дискретная математика
Добавлен: 28.11.2018
Просмотров: 6267
Скачиваний: 13

61
óÄëíú 4
äéåÅàçÄíéêàäÄ
1 Ç‚Ó‰Ì˚ Á‡Ï˜‡ÌËfl
По комбинаторике предусмотрено два тестовых задания и
одна контрольная задача.
Первое тестовое задание представлено задачей о шахмат-
ном городе. Для успешного его выполнения необходимо знать
основное правило комбинаторики (правило произведения) и
уметь применять формулу числа сочетаний без повторений.
Второе тестовое задание относится к применению комбина-
торики в теории вероятностей. Для выполнения этого задания
необходимо, кроме правила умножения и формулы числа соче-
таний, знать и другие формулы комбинаторики: число переста-
новок и размещений с повторением и без повторений.
В контрольной работе предусмотрено решение только од-
ной задачи, в основном из области комбинаторики двоичных
чисел. В отличие от тестов контрольная работа содержит задачу,
решение которой состоит из нескольких действий.
В следующих трех подразделах представлены образцы вы-
полнения тестовых заданий и приведен ряд задач с решениями,
относящихся к контрольным работам.
2 íÂÒÚ Ì‡ ÚÂÏÛ № 7: «Задача о шахматном городе»
Для тестирования по комбинаторике выбрана задача о шах-
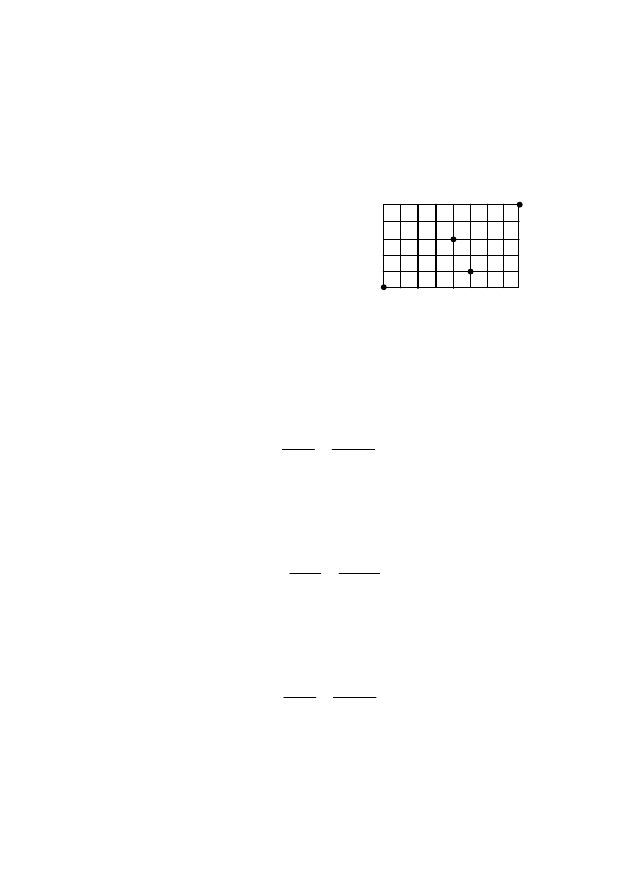
матном городе. Шахматный город размером 5×8 приведен на
рис. 1. На его площади, разграфленной вертикальными и гори-
зонтальными линиями, расположены точки, обозначенные бук-
вами A, B, C, D. Требуется определить число кратчайших путей,
ведущих от точки A до точки B и проходящих через точки C и D
(в заданном порядке). Движение возможно только по верти-
кальным и горизонтальным отрезкам.
Путь условимся обозначать упорядоченной последователь-
ностью букв, обозначающих точки на рис. 1: A-C-D-B. Согласно
записи A-C-D-B путь должен начаться в точке A, пройти через
точку C, затем — через точку D к точке B. При этом все вариан-
ты путей должны быть кратчайшими.
62
Это условие является одинаковым для всех вариантов дан-
ного тестового задания.
Пример 1. Найти число кратчайших путей вида A-C-D-B (рис. 1).
Решение. Сначала определим число кратчайших путей, ве-
дущих от точки A к точке C. Очевидно, что всякий кратчайший
путь состоит из трех вертикальных
отрезков и четырех горизонталь-
ных.
Обозначим вертикальные от-
резки единицами, а горизонталь-
ные — нулями. Тогда всякий путь
от A до C можно представить 7-
значным двоичным числом, содер-
жащим точно три единицы. Для нахождения количества этих 7-
значных чисел можно воспользоваться формулой числа сочета-
ний без повторений либо формулой числа перестановок с по-
вторениями. Согласно формуле числа сочетаний существует k
1
искомых чисел, где
3
1
7
7!
5 6 7
35.
4! 3!
1 2 3
k
С
⋅ ⋅
=
=
=
=
⋅
⋅ ⋅
Глядя на рис. 1, легко определить, что k
2
= 3, т.е. от точки C
до точки D ведут три пути, в каждом из которых два вертикаль-
ных отрезка и один горизонтальный.
Тот же результат дает формула числа сочетаний:
2
2
3
3!
1 2 3
3.
2! 1!
1 2 1
k
С
⋅ ⋅
=
=
=
=
⋅
⋅ ⋅
От точки D до точки B каждый кратчайший путь предста-
вится 7-значным двоичным числом, содержащим четыре едини-
цы и три нуля. Количество таких путей определим при помощи
формулы числа сочетаний без повторений:
4
3
7
7!
5 6 7
35.
3! 4!
1 2 3
k
С
⋅ ⋅
=
=
=
=
⋅
⋅ ⋅
Общее число k искомых путей определяется по основному
правилу комбинаторики — правилу произведения:
1
2
3
;
35 3 35
3675.
k
k k
k
k
= ⋅ ⋅
=
⋅ ⋅
=
Ответ: 3675.
Рис. 1
A
B
C
D

63
3 íÂÒÚ Ì‡ ÚÂÏÛ № 8: «íÂÓðËfl ‚ÂðÓflÚÌÓÒÚÂÈ»
Для выполнения задания по этой теме необходимы некото-
рые сведения из теории вероятностей. Объем этих сведений не-
велик. Вполне достаточно представления о вероятности как о
дроби, знаменатель которой показывает, сколько всего сущест-
вует исходов некоторого эксперимента, а числитель — сколько
из этих исходов удовлетворяют заданным условиям. Кроме это-
го, в некоторых случаях может оказаться полезным понятие
произведения вероятностей. Если рассматривается несколько
случайных событий и требуется найти вероятность того, что со-
стоятся все события, то сначала необходимо определить вероят-
ности каждого события, а затем найти произведение всех этих
вероятностей.
В общем случае события могут быть зависимыми и незави-
симыми. Если события независимы, то нахождение их вероят-
ностей обычно особых затруднений не вызывает. Если же собы-
тия зависимы, то потребуется лишь учесть то обстоятельство,
что если одно событие состоялось, то это необходимо учитывать
при нахождении вероятности второго события. В таких случаях
пользуются не очень удачным термином «условная вероят-
ность». Здесь слово «условная» говорит не о том, что мы о чем-
то собираемся условиться (договориться). Оно обозначает лишь
следующее: вероятность второго события определяется при ус-
ловии, что первое событие состоялось.
Все особенности, относящиеся к вычислению вероятностей
в пределах темы данного теста, рассмотрим на примерах.
Пример 1. Монету подбрасывают 8 раз. Найти вероятность
того, что первым выпадет герб и последним также выпадет герб.
Решение. Вероятность того, что первым выпадет герб, рав-
на 1/2. Вероятность того, что при последнем подбрасывании
монеты выпадет герб, также равна 1/2. Оба эти события незави-
симы. Следовательно,
1 1
1
.
2 2
4
p
= ⋅ =
Ответ: p = 1/4.

64
Пример 2. Игральную кость подбрасывают 2 раза. Найти
вероятность того, что второе выпавшее число будет в 2 раза
больше первого.
Решение. Первый бросок может закончиться шестью исхо-
дами, и второй шестью. Следовательно, число всех исходов экс-
перимента равно 36. Это знаменатель искомой вероятности.
Числитель равен 3. Это исходы 1 и 2, 2 и 4, 3 и 6. Таким обра-
зом, искомая вероятность равна 1/12.
Ответ: 1/12.
Пример 3. Некто задумал двузначное десятичное число N
(с нуля двузначные числа не начинается). Найти вероятность
того, что если каждую цифру представить в двоичном коде
8421, то в восьмизначном двоично-десятичном коде будет точно
две единицы.
Решение. Всего двузначных десятичных чисел, не начи-
нающихся с нуля, существует 90: 10, 11, 12, .., 99. Это знамена-
тель искомой вероятности. Определим числитель. В двоично-
десятичном коде каждая десятичная цифра заменяется тетрадой —
четырехзначным двоичным кодом. Например:
35|
10
= 00110101|
2
; 48|
10
= 01001000|
2
; 30|
10
= 00110000|
2
.
Если две единицы находятся в первой тетраде, то во второй
их нет. Всего существует шесть тетрад с двумя единицами. Че-
тырьмя тетрадами кодируются десятичные цифры 3, 5, 6 и 9,
следовательно, существует четыре двоично-десятичных кода,
оканчивающихся четырьмя нулями:
00110000, 01010000, 01100000, 10010000.
Если в первой тетраде одна единица, то и во второй одна.
Это тетрады вида: 0001, 0010, 0100, 1000. Из них можно соста-
вить 16 двоично-десятичных кодов:
00010001, 00100001, 01000001, 10000001,
00010010, 00100010, 01000010, 10000010,
00010100, 00100100, 01000100, 10000100,
00011000, 00101000, 01001000, 10001000.
Таким образом, всего существует 20 двоично-десятичных
кодов, в каждом из которых точно две единицы. Искомая веро-
ятность равна 20/90. После сокращения: 2/9.
Ответ: 2/9.

65
Пример 3. В тире три мишени. Перед мишенями пять
стрелков. Каждый стрелок самостоятельно, независимо от дру-
гих, выбирает мишень и производит один выстрел без промаха.
Найти вероятность того, что поражена будет только одна ми-
шень (пятью выстрелами).
Решение. Пронумеруем мишени цифрами троичной систе-
мы 0, 1, 2 и поставим в соответствие каждому исходу стрельбы
пятизначное троичное число. Например, код 10021 обозначает:
первый стрелок выбрал первую мишень, второй и третий — ну-
левую, четвертый — вторую, пятый — первую. Всего существу-
ет 3
5
= 243 пятизначных троичных кодов, которые могут начи-
наться с нуля. Столько же существует и исходов стрельбы. Это
знаменатель искомой вероятности. Определим числитель. Всего
существует только три исхода стрельбы, когда поражена одна
мишень из трех. Им соответствуют коды: 00000 — все пули по-
пали в нулевую мишень, 11111 — все пули попали в первую
мишень, 22222 — все пули попали в вторую мишень. Искомая
вероятность равна 3/242. После сокращения на 3 получаем 1/81.
Ответ: 1/81.
Пример 4. В урне 4 белых и 8 черных шаров. Найти веро-
ятность того, что если наугад извлечь 4 шара, то два из них бу-
дут белыми и два черными.
Решение. Всего шаров 12. Из них 4 шара можно выбрать
4
12
12!
9 10 11 12
495
8! 4!
1 2 3 4
С
⋅ ⋅ ⋅
=
=
=
⋅
⋅ ⋅ ⋅
способами. Это знаменатель искомой вероятности. Для выбора
двух черных шаров из восьми существует
2
8
28
С
=
вариантов.
Выбор двух белых шаров из четырех возможен
2
4
6
С
= способа-
ми. Тогда искомая вероятность равна:
28 6
56
.
495
165
p
⋅
=
=
Ответ: 56/165.