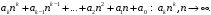Файл: Рекомендации по выполнению контрольной работы по дисциплине Математический анализ.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 06.11.2023
Просмотров: 58
Скачиваний: 2
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Для вычисления определенного интеграла используют формулу Ньютона – Лейбница
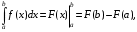
где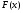 – первообразная функция для
– первообразная функция для 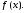
При использовании метода замены переменной (или метода подстановки) определенный интеграл вычисляют по формуле
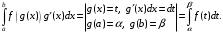
При нахождении определенного интеграла с помощью метода интегрирования по частям используют формулу
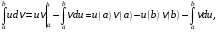 (2)
(2)
где
 – функции, дифференцируемые на
– функции, дифференцируемые на 
Задания 3.1 – 3.2. Несобственный интеграл от функции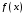 по бес-
по бес-
конечному промежутку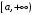 (или несобственный интеграл первого рода) определяется равенством
(или несобственный интеграл первого рода) определяется равенством
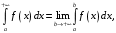
Если указанный предел существует, то интеграл называется сходящимся, в противном случае – расходящимся. Если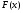 – первообразная функции
– первообразная функции 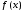 , то верна формула
, то верна формула
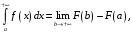
Аналогично определяется несобственный интеграл от функции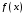 по бесконечному промежутку
по бесконечному промежутку 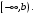 В случае сходимости верна формула
В случае сходимости верна формула
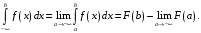
Задания 5.1 – 5.2. Дифференциальное уравнение вида
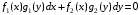
называется уравнением с разделяющимися переменными.
Предполагая, что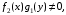 почленным делением на
почленным делением на 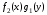 его сводят к уравнению
его сводят к уравнению
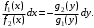
Далее равенство интегрируют и получают общий интеграл.
Линейное однородное дифференциальное уравнение n-го порядка с постоянными коэффициентами имеет вид
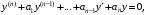
где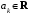
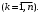
Общим решением этого уравнения является функция
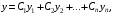
где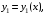
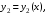 …,
…, 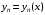 – линейно независимые частные решения;
– линейно независимые частные решения; 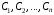 – произвольные постоянные.
– произвольные постоянные.
Для нахождения частных решений данного уравнения составляют характеристическое уравнение
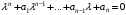
и решают его.
Каждому корню характеристического уравнения соответствует определенное частное решение:
а) если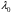 – простой действительный корень, то ему соответствует решение вида
– простой действительный корень, то ему соответствует решение вида
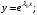 (4)
(4)
б) если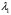 – действительный корень кратностью k
– действительный корень кратностью k 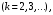 то ему соответствует k частных решений
то ему соответствует k частных решений
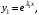
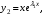 …,
…, 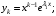 (5)
(5)
в) если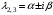 – пара комплексно-сопряженных корней, то им соответствуют два частных решения:
– пара комплексно-сопряженных корней, то им соответствуют два частных решения:
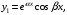
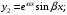 (6)
(6)
г) если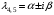 – пара комплексно-сопряженных корней кратностью k
– пара комплексно-сопряженных корней кратностью k  то им соответствуют
то им соответствуют 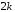 частных решения:
частных решения:
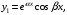
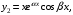 …,
…, 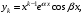
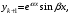
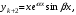 …,
…,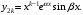
Задания 6.1 – 6.2. Дифференциальное уравнение вида
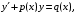
где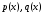 – заданные непрерывные функции, называется линейным дифференциальным уравнением первого порядка.
– заданные непрерывные функции, называется линейным дифференциальным уравнением первого порядка.
Метод Бернулли. Для решения линейного дифференциального уравнения первого порядка необходимо:
1) искать общее решение уравнения в виде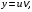 где
где 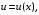
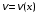 – функции, которые надо найти;
– функции, которые надо найти;
2) подставить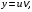
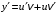 в заданное уравнение;
в заданное уравнение;
3) записать уравнение в виде
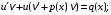
4) найти функцию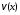 как частное решение дифференциального уравнения
как частное решение дифференциального уравнения 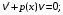
5) найти общее решение уравнения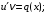
6) записать общее решение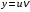 исходного уравнения для найденных функций u, v.
исходного уравнения для найденных функций u, v.
Задачей Коши для дифференциального уравнения первого порядка называется задача нахождения частного решения дифференциального уравнения, удовлетворяющего заданному начальному условию
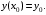
Рис. 2
Если область интегрирования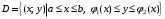 – правильная в отношении оси
– правильная в отношении оси 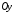 (рис. 14), то
(рис. 14), то
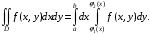
Если область интегрирования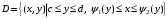 – правильная в отношении оси
– правильная в отношении оси 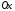 (рис. 15), то
(рис. 15), то
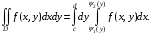
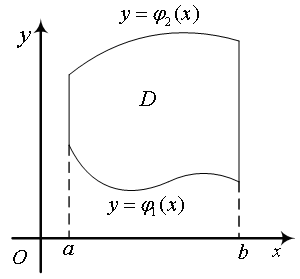
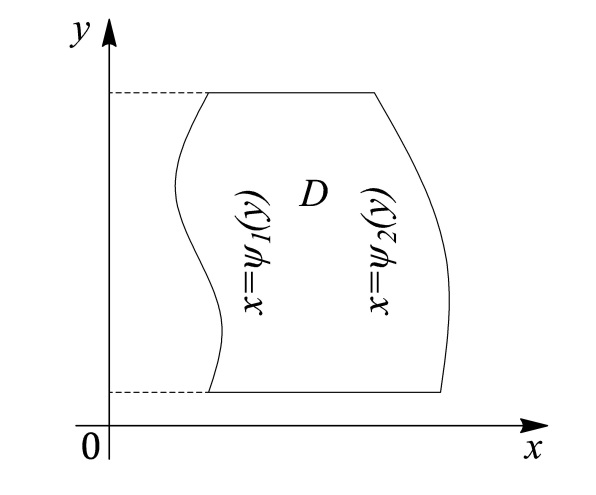 Рис. 3 Рис. 4
Рис. 3 Рис. 4
Задания 8.1 – 8.2. Числовым рядом называется выражение вида
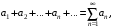
где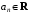
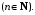
Сумма
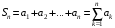
называется n-й частичной суммой.
Если существует предел
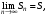
то ряд называется сходящимся, а S – его суммой; пишут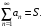
Если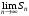 не существует, то ряд называется расходящимся.
не существует, то ряд называется расходящимся.
Необходимый признак сходимости. Если ряд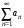 сходится, то
сходится, то
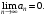
Следствие необходимого признака сходимости. Если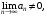 то ряд
то ряд  расходится.
расходится.
Признак сравнения. Пусть для знакоположительных рядов и
и 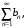 начиная с некоторого n
начиная с некоторого n 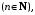 выполняется неравенство
выполняется неравенство
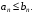
Тогда:
а) из сходимости ряда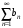 следует сходимость ряда
следует сходимость ряда 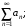
б) из расходимости ряда следует расходимость ряда
следует расходимость ряда 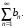
Предельный признак сравнения. Если для знакоположительных рядов и
и 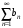 существует
существует
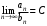
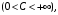
то оба эти ряда сходятся или оба расходятся.
Для исследования по признаку сравнения или предельному признаку сравнения часто используют следующие ряды:
а) ряд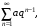 сходящийся при
сходящийся при 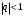 и расходящийся при
и расходящийся при 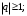
б) ряд Дирихле (обобщенный гармонический ряд)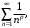 сходящийся при
сходящийся при 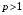 и расходящийся при
и расходящийся при 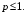
Если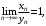 то последовательности
то последовательности 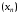 и
и 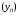 называются эквивалентными, что обозначают
называются эквивалентными, что обозначают 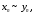
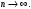
В частности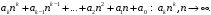
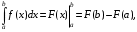
где
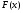 – первообразная функция для
– первообразная функция для 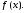
При использовании метода замены переменной (или метода подстановки) определенный интеграл вычисляют по формуле
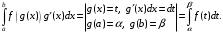
При нахождении определенного интеграла с помощью метода интегрирования по частям используют формулу
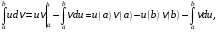 (2)
(2)где

 – функции, дифференцируемые на
– функции, дифференцируемые на 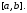
Задания 3.1 – 3.2. Несобственный интеграл от функции
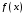 по бес-
по бес-конечному промежутку
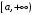 (или несобственный интеграл первого рода) определяется равенством
(или несобственный интеграл первого рода) определяется равенством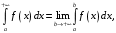
Если указанный предел существует, то интеграл называется сходящимся, в противном случае – расходящимся. Если
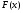 – первообразная функции
– первообразная функции 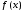 , то верна формула
, то верна формула 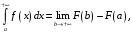
Аналогично определяется несобственный интеграл от функции
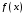 по бесконечному промежутку
по бесконечному промежутку 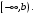 В случае сходимости верна формула
В случае сходимости верна формула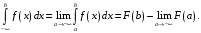
| Задания 4.1 – 4.2. Площадь плоской фигуры D (рис. 1), ограниченной кривыми 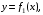 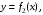 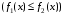 и прямыми и прямыми 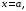 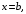 находится по формуле находится по формуле 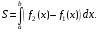 (3) (3) | 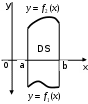 Рис. 1 |
Задания 5.1 – 5.2. Дифференциальное уравнение вида
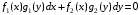
называется уравнением с разделяющимися переменными.
Предполагая, что
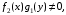 почленным делением на
почленным делением на 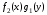 его сводят к уравнению
его сводят к уравнению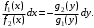
Далее равенство интегрируют и получают общий интеграл.
Линейное однородное дифференциальное уравнение n-го порядка с постоянными коэффициентами имеет вид
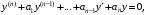
где
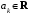
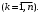
Общим решением этого уравнения является функция
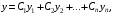
где
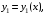
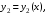 …,
…, 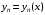 – линейно независимые частные решения;
– линейно независимые частные решения; 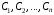 – произвольные постоянные.
– произвольные постоянные.Для нахождения частных решений данного уравнения составляют характеристическое уравнение
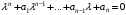
и решают его.
Каждому корню характеристического уравнения соответствует определенное частное решение:
а) если
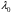 – простой действительный корень, то ему соответствует решение вида
– простой действительный корень, то ему соответствует решение вида 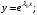 (4)
(4)б) если
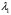 – действительный корень кратностью k
– действительный корень кратностью k 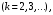 то ему соответствует k частных решений
то ему соответствует k частных решений 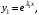
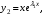 …,
…, 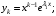 (5)
(5)в) если
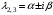 – пара комплексно-сопряженных корней, то им соответствуют два частных решения:
– пара комплексно-сопряженных корней, то им соответствуют два частных решения:
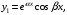
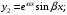 (6)
(6)г) если
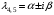 – пара комплексно-сопряженных корней кратностью k
– пара комплексно-сопряженных корней кратностью k  то им соответствуют
то им соответствуют 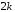 частных решения:
частных решения: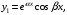
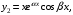 …,
…, 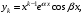
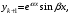
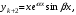 …,
…,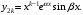
Задания 6.1 – 6.2. Дифференциальное уравнение вида
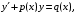
где
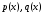 – заданные непрерывные функции, называется линейным дифференциальным уравнением первого порядка.
– заданные непрерывные функции, называется линейным дифференциальным уравнением первого порядка.Метод Бернулли. Для решения линейного дифференциального уравнения первого порядка необходимо:
1) искать общее решение уравнения в виде
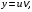 где
где 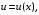
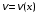 – функции, которые надо найти;
– функции, которые надо найти;2) подставить
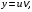
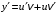 в заданное уравнение;
в заданное уравнение;3) записать уравнение в виде
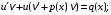
4) найти функцию
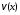 как частное решение дифференциального уравнения
как частное решение дифференциального уравнения 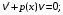
5) найти общее решение уравнения
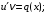
6) записать общее решение
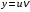 исходного уравнения для найденных функций u, v.
исходного уравнения для найденных функций u, v.Задачей Коши для дифференциального уравнения первого порядка называется задача нахождения частного решения дифференциального уравнения, удовлетворяющего заданному начальному условию
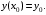
| Задания 7.1 – 7.2. Объем V цилиндрического тела T, ограниченного сверху поверхностью 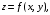 снизу плоскостью снизу плоскостью 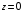 и сбоку цилиндрической поверхностью (рис. 2), вычисляют по формуле: и сбоку цилиндрической поверхностью (рис. 2), вычисляют по формуле: 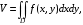 (7) (7)где область D – проекция тела на плоскость 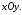 | 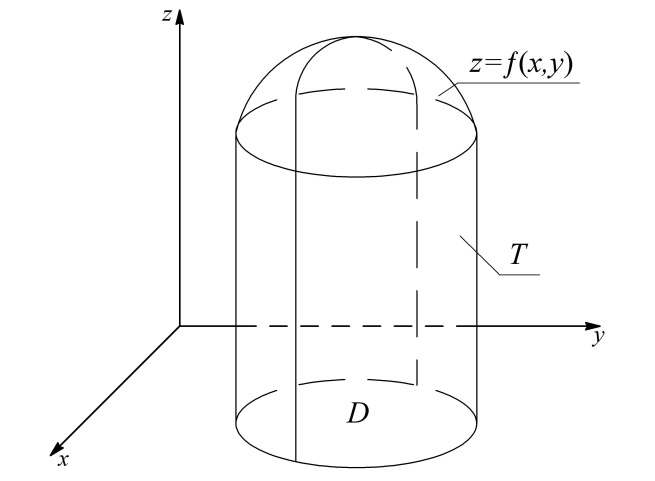 |
Рис. 2
Если область интегрирования
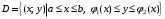 – правильная в отношении оси
– правильная в отношении оси 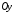 (рис. 14), то
(рис. 14), то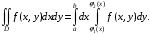
Если область интегрирования
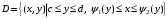 – правильная в отношении оси
– правильная в отношении оси 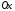 (рис. 15), то
(рис. 15), то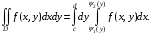

 Рис. 3 Рис. 4
Рис. 3 Рис. 4Задания 8.1 – 8.2. Числовым рядом называется выражение вида
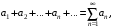
где
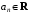
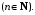
Сумма
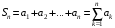
называется n-й частичной суммой.
Если существует предел
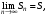
то ряд называется сходящимся, а S – его суммой; пишут
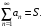
Если
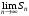 не существует, то ряд называется расходящимся.
не существует, то ряд называется расходящимся.Необходимый признак сходимости. Если ряд
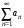 сходится, то
сходится, то
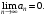
Следствие необходимого признака сходимости. Если
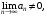 то ряд
то ряд  расходится.
расходится.Признак сравнения. Пусть для знакоположительных рядов
 и
и 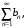 начиная с некоторого n
начиная с некоторого n 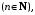 выполняется неравенство
выполняется неравенство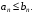
Тогда:
а) из сходимости ряда
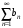 следует сходимость ряда
следует сходимость ряда 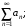
б) из расходимости ряда
 следует расходимость ряда
следует расходимость ряда 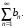
Предельный признак сравнения. Если для знакоположительных рядов
 и
и 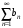 существует
существует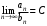
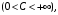
то оба эти ряда сходятся или оба расходятся.
Для исследования по признаку сравнения или предельному признаку сравнения часто используют следующие ряды:
а) ряд
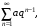 сходящийся при
сходящийся при 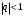 и расходящийся при
и расходящийся при 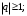
б) ряд Дирихле (обобщенный гармонический ряд)
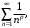 сходящийся при
сходящийся при 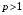 и расходящийся при
и расходящийся при 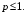
Если
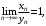 то последовательности
то последовательности 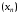 и
и 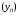 называются эквивалентными, что обозначают
называются эквивалентными, что обозначают 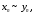
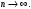
В частности