Файл: Рекомендации по выполнению контрольной работы по дисциплине Математический анализ.docx

Решение. Найдем радиус сходимости данного ряда. Выпишем коэффициенты -го и 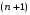-го членов ряда.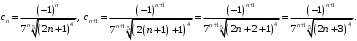



Тогда







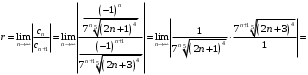
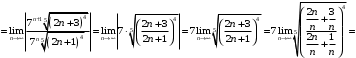
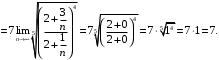
Радиус сходимости 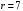. Так как ряд задан как степенной относительно основания 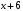( 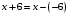), то центр интервала сходимости 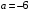. Ряд абсолютно сходится для всех значений из интервала 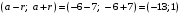. Для значений 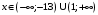ряд расходится. Исследуем поведение ряда на концах интервала сходимости, т. е. пр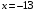и и .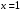

Подставляем в заданный степенной ряд :





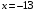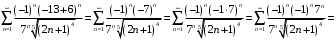
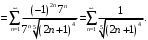
Получили знакоположительный ряд. Сравним его с рядом Дирихле.

Поскольку 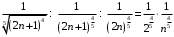при и ряд 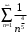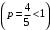расходится, то исследуемый числовой ряд расходится. Это означает, что степенной ряд расходится в точке .

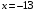Таким образом, ряд 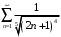расходится по предельному признаку сравнения, так как расходится ряд .

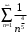Подставим в заданный степенной ряд :



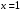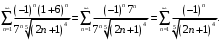
Получили знакочередующийся числовой ряд. Составим ряд из модулей его членов:

---

. Этот ряд расходится, как и ряд Дирихле ( 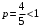). Значит, полученный при знакочередующийся ряд не сходится абсолютно. Исследуем на условную сходимость. Применим признак Лейбница.

Имеем



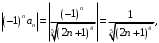
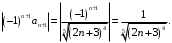
Так как 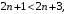то 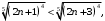тогда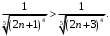

Таким образом, 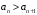, т. е. выполняется первое условие признака Лейбница. Поскольку 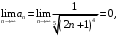то выполняется и второе условие

теоремы Лейбница. Следовательно, ряд 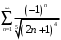сходится условно.

Окончательно получим, что степенной ряд 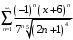сходится при 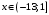, причем при 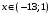сходится абсолютно, а при – условно.

Задание 10. Вычислить определенный интеграл с точностью до 0,001, разложив подынтегральную функцию в ряд Маклорена.



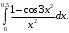
Решение. Разложим функцию 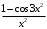в степенной ряд. Для любых имеет место разложение в ряд Маклорена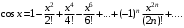



Тогда













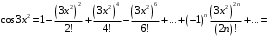
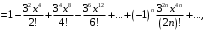
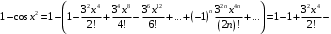
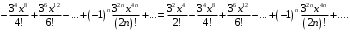
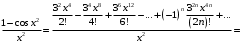
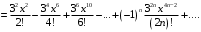
Почленно интегрируем полученный ряд:

---

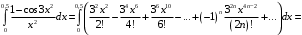
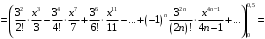
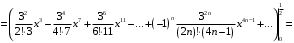
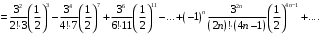
В итоге получаем знакочередующийся ряд



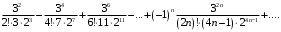
Интеграл 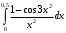равен сумме найденного знакочередующегося ряда. Найдем приближенное значение этой суммы с требуемой точностью. Поскольку для полученного знакочередующегося ряда выполняются условия теоремы Лейбница, то остаток этого ряда по абсолютной величине не превосходит модуля первого из отброшенных членов.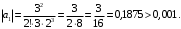







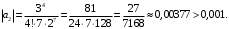
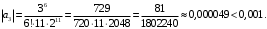
Так как 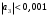, то с точностью до 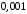имеем

---