Файл: Рекомендации по выполнению контрольной работы по дисциплине Математический анализ.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 06.11.2023
Просмотров: 50
Скачиваний: 2
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
, а внешнее по  . Для того, чтобы расставить пределы интегрирования, проведем через область
. Для того, чтобы расставить пределы интегрирования, проведем через область  прямые, параллельные оси
прямые, параллельные оси  . Они пересекут сначала дугу параболы
. Они пересекут сначала дугу параболы  затем прямую
затем прямую  . Следовательно, линией входа в область
. Следовательно, линией входа в область  будет
будет  , а линией выхода
, а линией выхода  . При этом область
. При этом область  проектируется на отрезок
проектируется на отрезок 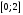 оси
оси  , т. е.
, т. е. 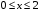 . Получим
. Получим
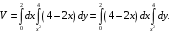
Сначала вычисляется внутренний интеграл, а затем внешний интеграл (из-под внутреннего интеграла вынесли множитель, который не зависит от ):
):
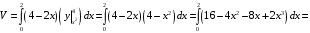
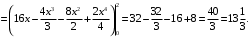
Так как область является правильной в отношении обеих координатных осей, то переходя к повторному (двукратному) интегралу можно выполнить внутреннее интегрирование по
является правильной в отношении обеих координатных осей, то переходя к повторному (двукратному) интегралу можно выполнить внутреннее интегрирование по  , а внешнее – по
, а внешнее – по  . Для того чтобы расставить пределы интнгрирования, проведем через область
. Для того чтобы расставить пределы интнгрирования, проведем через область  прямые, параллельные оси
прямые, параллельные оси  . Они пересекут сначала прямую
. Они пересекут сначала прямую 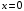 , затем дугу параболы
, затем дугу параболы 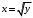 . Следовательно, линией входа в область
. Следовательно, линией входа в область  будет
будет 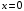 , а линией выхода
, а линией выхода 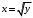
. При этом область проектируется на отрезок
проектируется на отрезок 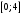 оси
оси  , т. е.
, т. е. 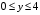 . Получим
. Получим
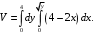
Сначала вычислим внутренний интеграл, а затем внешний интеграл.
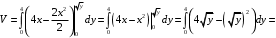
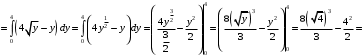
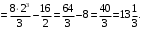
Ответ: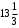 .
.
б) Данное тело (рис. 8) ограничено сверху частью параболического цилиндра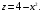 Боковая поверхность образована в результате пересечения плоскостей
Боковая поверхность образована в результате пересечения плоскостей 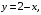

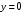 (плоскость
(плоскость 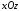 ), а снизу – плоскостью
), а снизу – плоскостью 
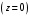 . Проекция тела на плоскость
. Проекция тела на плоскость  (область
(область  ) представляет собой треугольник, ограниченный прямыми
) представляет собой треугольник, ограниченный прямыми 
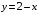 и
и 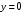 (ось
(ось  ) (рис. 9). Этот треугольник ограничивает тело снизу.
) (рис. 9). Этот треугольник ограничивает тело снизу.
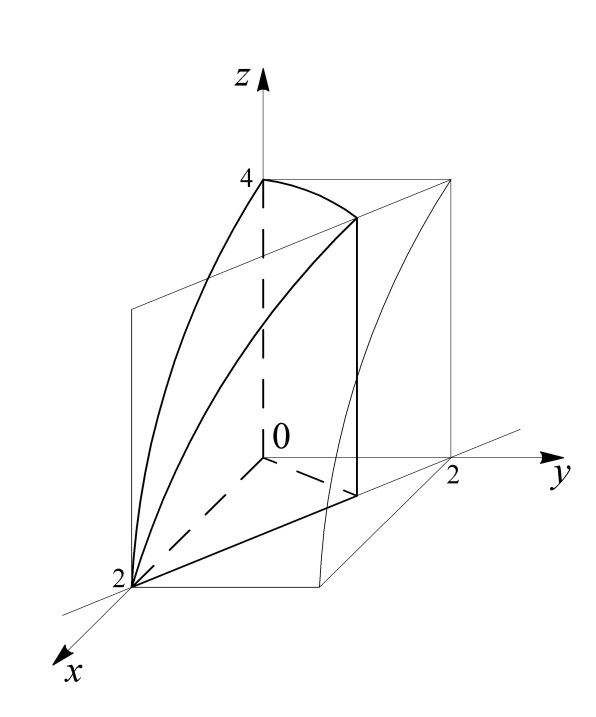
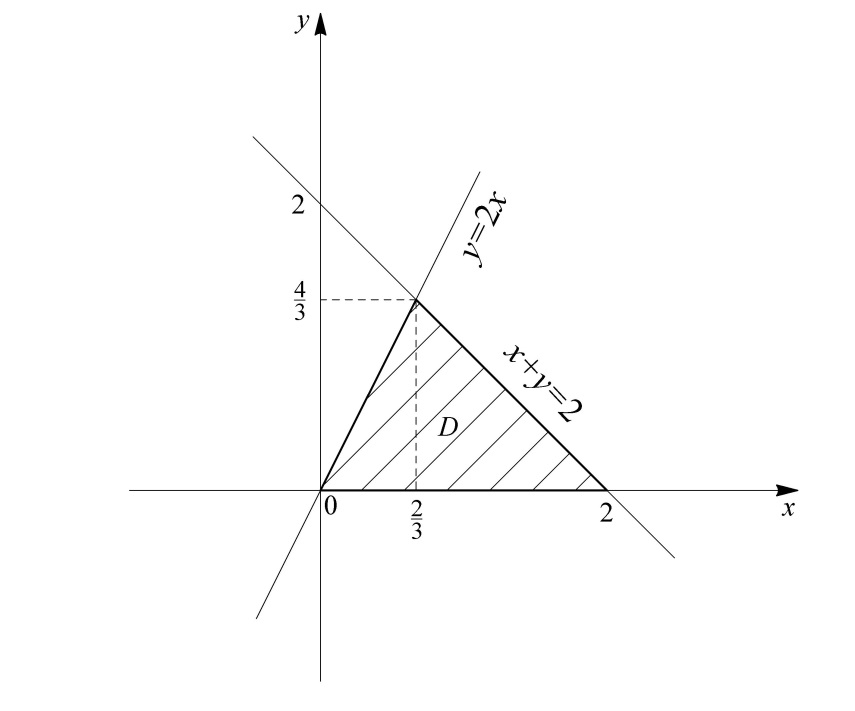
Рис. 8 Рис. 9
Объем тела вычисляется по формуле (7):
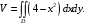
Область является правильной в отношении оси
является правильной в отношении оси  .
.
Переходим к повторному (двукратному) интегралу и выполним внутреннее интегрирование по
, а внешнее – по . Запишем границы области
. Запишем границы области  в виде
в виде 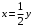 ,
, 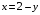 . Найдем отрезок на оси
. Найдем отрезок на оси  , на который проектируется область
, на который проектируется область  . Решая совместно уравнения
. Решая совместно уравнения 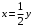 и
и 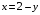 , находим координаты точки пересечения прямых:
, находим координаты точки пересечения прямых: 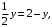
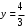 . Область
. Область  проектируется на отрезок
проектируется на отрезок 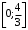 оси
оси  , т. е.
, т. е. 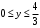 . Для того чтобы расставить пределы интегрирования, проведем через область
. Для того чтобы расставить пределы интегрирования, проведем через область  прямые, параллельные оси
прямые, параллельные оси  . Они пересекут сначала прямую
. Они пересекут сначала прямую 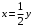 , затем прямую
, затем прямую 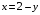 . Следовательно, линией входа в область
. Следовательно, линией входа в область  будет
будет 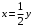
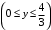 , а линией выхода будет
, а линией выхода будет 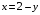
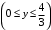 . Получим
. Получим
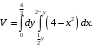
Вычислим сначала внутренний интеграл, а затем внешний интеграл.
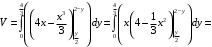
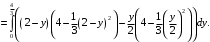
Преобразуем подынтегральное выражение и приходим к интегралу, который вычисляем:
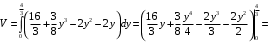
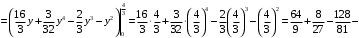
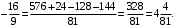
Ответ: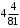 .
.
Задание 8. Исследовать ряд на сходимость:
а)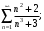 б)
б) 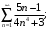 в)
в) 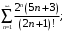 г)
г) 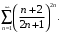
Решение. а) Для исследования на сходимость применим предельный признак сравнения. Сравним данный ряд с рядом Дирихле (обобщенным гармоническим рядом)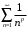 . Для определения показателя
. Для определения показателя 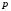 рассмотрим общий член заданного ряда
рассмотрим общий член заданного ряда 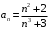 . Если
. Если 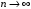 , то «скорость роста» числителя и знаменателя задают их старшие степени. Находим
, то «скорость роста» числителя и знаменателя задают их старшие степени. Находим 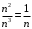 , поэтому
, поэтому 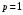 . Следовательно, сравниваем данный ряд с расходящимся гармоническим рядом
. Следовательно, сравниваем данный ряд с расходящимся гармоническим рядом 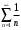 , общий член которого
, общий член которого 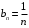 . Вычислим предел
. Вычислим предел
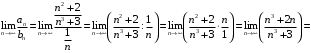
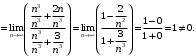
Так как гармонический ряд расходится, то по предельному прзнаку сравнения расходится ряд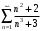 .
.
б) 1-й способ. Для исследования на сходимость применим признак сравнения. Так как
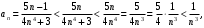
то сравним данный ряд со сходящимся рядом Дирихле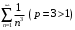 . Общий
. Общий
член ряда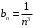 . Поскольку выполняется неравенство
. Поскольку выполняется неравенство 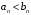 , то по признаку сравнения ряд
, то по признаку сравнения ряд 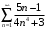 также сходится.
также сходится.
2-й способ. Для исследования на сходимость данного ряда можно применить предельный признак сравнения. Сравним данный ряд с рядом Дирихле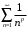 . Для определения показателя
. Для определения показателя
 рассмотрим общий член заданного ряда и определим выражение, к которому он эквивалентен, если
рассмотрим общий член заданного ряда и определим выражение, к которому он эквивалентен, если  .
.
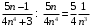 , где
, где 
Следовательно, сравниваем данный ряд с рядом Дирихле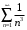 . Этот ряд сходится, так как
. Этот ряд сходится, так как 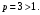 Общий член этого ряда
Общий член этого ряда  . Значит, и заданный ряд сходится. Вычислим предел отношения
. Значит, и заданный ряд сходится. Вычислим предел отношения
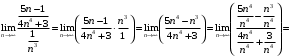
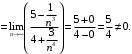
По предельному признаку сравнения из сходимости ряда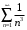 следует сходимость ряда
следует сходимость ряда  .
.
в) Применим признак Д’Аламбера, который является наиболее рациональным в случае присутствия факториала. Так как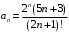 ,
, 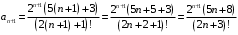 , то имеем
, то имеем
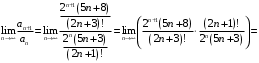
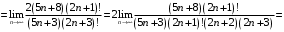
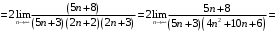
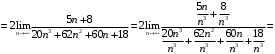
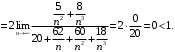
Таким образом, по признаку Д’Аламбера ряд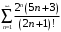 сходится.
сходится.
г) Применим признак Коши. Вычислим предел
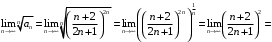
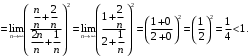
Отсюда следует, что по признаку Коши ряд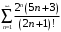 сходится.
сходится.
Задание 9. Найти радиус и область сходимости степенного ряда, установить тип сходимости (абсолютная, условная сходимость):
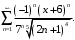
 . Для того, чтобы расставить пределы интегрирования, проведем через область
. Для того, чтобы расставить пределы интегрирования, проведем через область  прямые, параллельные оси
прямые, параллельные оси  . Они пересекут сначала дугу параболы
. Они пересекут сначала дугу параболы  затем прямую
затем прямую  . Следовательно, линией входа в область
. Следовательно, линией входа в область  будет
будет  , а линией выхода
, а линией выхода  . При этом область
. При этом область  проектируется на отрезок
проектируется на отрезок 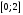 оси
оси  , т. е.
, т. е. 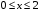 . Получим
. Получим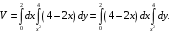
Сначала вычисляется внутренний интеграл, а затем внешний интеграл (из-под внутреннего интеграла вынесли множитель, который не зависит от
 ):
):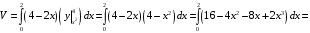
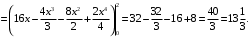
Так как область
 является правильной в отношении обеих координатных осей, то переходя к повторному (двукратному) интегралу можно выполнить внутреннее интегрирование по
является правильной в отношении обеих координатных осей, то переходя к повторному (двукратному) интегралу можно выполнить внутреннее интегрирование по  , а внешнее – по
, а внешнее – по  . Для того чтобы расставить пределы интнгрирования, проведем через область
. Для того чтобы расставить пределы интнгрирования, проведем через область  прямые, параллельные оси
прямые, параллельные оси  . Они пересекут сначала прямую
. Они пересекут сначала прямую 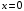 , затем дугу параболы
, затем дугу параболы 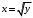 . Следовательно, линией входа в область
. Следовательно, линией входа в область  будет
будет 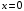 , а линией выхода
, а линией выхода 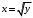
. При этом область
 проектируется на отрезок
проектируется на отрезок 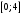 оси
оси  , т. е.
, т. е. 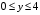 . Получим
. Получим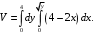
Сначала вычислим внутренний интеграл, а затем внешний интеграл.
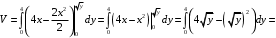
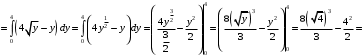
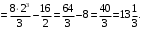
Ответ:
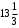 .
.б) Данное тело (рис. 8) ограничено сверху частью параболического цилиндра
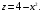 Боковая поверхность образована в результате пересечения плоскостей
Боковая поверхность образована в результате пересечения плоскостей 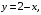

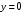 (плоскость
(плоскость 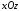 ), а снизу – плоскостью
), а снизу – плоскостью 
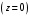 . Проекция тела на плоскость
. Проекция тела на плоскость  (область
(область  ) представляет собой треугольник, ограниченный прямыми
) представляет собой треугольник, ограниченный прямыми 
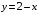 и
и 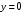 (ось
(ось  ) (рис. 9). Этот треугольник ограничивает тело снизу.
) (рис. 9). Этот треугольник ограничивает тело снизу. 

Рис. 8 Рис. 9
Объем тела вычисляется по формуле (7):
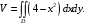
Область
 является правильной в отношении оси
является правильной в отношении оси  .
. Переходим к повторному (двукратному) интегралу и выполним внутреннее интегрирование по

, а внешнее – по
 . Запишем границы области
. Запишем границы области  в виде
в виде 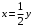 ,
, 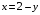 . Найдем отрезок на оси
. Найдем отрезок на оси  , на который проектируется область
, на который проектируется область  . Решая совместно уравнения
. Решая совместно уравнения 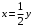 и
и 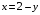 , находим координаты точки пересечения прямых:
, находим координаты точки пересечения прямых: 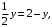
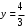 . Область
. Область  проектируется на отрезок
проектируется на отрезок 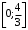 оси
оси  , т. е.
, т. е. 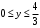 . Для того чтобы расставить пределы интегрирования, проведем через область
. Для того чтобы расставить пределы интегрирования, проведем через область  прямые, параллельные оси
прямые, параллельные оси  . Они пересекут сначала прямую
. Они пересекут сначала прямую 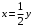 , затем прямую
, затем прямую 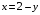 . Следовательно, линией входа в область
. Следовательно, линией входа в область  будет
будет 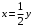
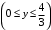 , а линией выхода будет
, а линией выхода будет 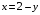
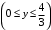 . Получим
. Получим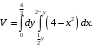
Вычислим сначала внутренний интеграл, а затем внешний интеграл.
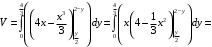
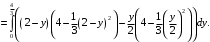
Преобразуем подынтегральное выражение и приходим к интегралу, который вычисляем:
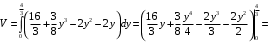
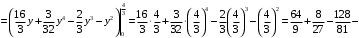
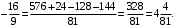
Ответ:
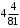 .
.Задание 8. Исследовать ряд на сходимость:
а)
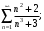 б)
б) 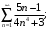 в)
в) 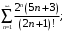 г)
г) 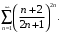
Решение. а) Для исследования на сходимость применим предельный признак сравнения. Сравним данный ряд с рядом Дирихле (обобщенным гармоническим рядом)
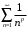 . Для определения показателя
. Для определения показателя 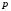 рассмотрим общий член заданного ряда
рассмотрим общий член заданного ряда 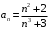 . Если
. Если 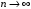 , то «скорость роста» числителя и знаменателя задают их старшие степени. Находим
, то «скорость роста» числителя и знаменателя задают их старшие степени. Находим 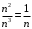 , поэтому
, поэтому 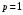 . Следовательно, сравниваем данный ряд с расходящимся гармоническим рядом
. Следовательно, сравниваем данный ряд с расходящимся гармоническим рядом 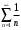 , общий член которого
, общий член которого 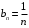 . Вычислим предел
. Вычислим предел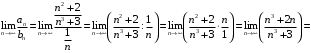
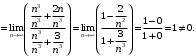
Так как гармонический ряд расходится, то по предельному прзнаку сравнения расходится ряд
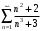 .
.б) 1-й способ. Для исследования на сходимость применим признак сравнения. Так как
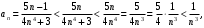
то сравним данный ряд со сходящимся рядом Дирихле
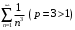 . Общий
. Общий член ряда
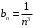 . Поскольку выполняется неравенство
. Поскольку выполняется неравенство 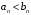 , то по признаку сравнения ряд
, то по признаку сравнения ряд 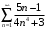 также сходится.
также сходится.2-й способ. Для исследования на сходимость данного ряда можно применить предельный признак сравнения. Сравним данный ряд с рядом Дирихле
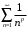 . Для определения показателя
. Для определения показателя
 рассмотрим общий член заданного ряда и определим выражение, к которому он эквивалентен, если
рассмотрим общий член заданного ряда и определим выражение, к которому он эквивалентен, если  .
. 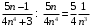 , где
, где 
Следовательно, сравниваем данный ряд с рядом Дирихле
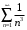 . Этот ряд сходится, так как
. Этот ряд сходится, так как 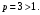 Общий член этого ряда
Общий член этого ряда  . Значит, и заданный ряд сходится. Вычислим предел отношения
. Значит, и заданный ряд сходится. Вычислим предел отношения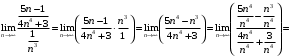
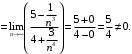
По предельному признаку сравнения из сходимости ряда
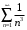 следует сходимость ряда
следует сходимость ряда  .
.в) Применим признак Д’Аламбера, который является наиболее рациональным в случае присутствия факториала. Так как
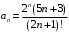 ,
, 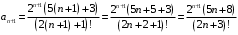 , то имеем
, то имеем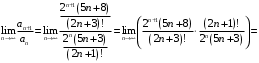
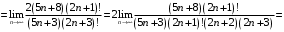
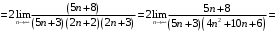
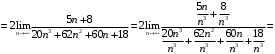
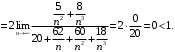
Таким образом, по признаку Д’Аламбера ряд
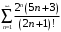 сходится.
сходится.г) Применим признак Коши. Вычислим предел
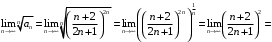
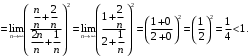
Отсюда следует, что по признаку Коши ряд
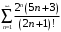 сходится.
сходится.Задание 9. Найти радиус и область сходимости степенного ряда, установить тип сходимости (абсолютная, условная сходимость):