Файл: Рекомендации по выполнению контрольной работы по дисциплине Математический анализ.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 06.11.2023
Просмотров: 57
Скачиваний: 2
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Предельный признак Д’Аламбера. Пусть для знакоположительного ряда
 существует
существует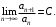
Тогда:
а) при
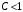 ряд сходится;
ряд сходится;б) при
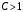 ряд расходится.
ряд расходится.Предельный признак Коши. Пусть для знакоположительного ряда
 существует
существует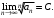
Тогда:
а) при
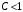 ряд сходится;
ряд сходится;б) при
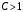 ряд расходится.
ряд расходится.Если в предельных признаках Д’Аламбера и Коши получаем
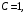 то нужны дополнительные исследования по другим признакам.
то нужны дополнительные исследования по другим признакам.При использовании предельного признака Коши часто применяют формулу
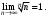
Интегральный критерий сходимости. Пусть члены ряда
 имеют вид
имеют вид 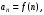 где
где 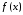 – неотрицательная монотонно убывающая на
– неотрицательная монотонно убывающая на 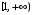 функция. Ряд сходится (расходится) тогда и только тогда, когда сходится (расходится) несобственный интеграл
функция. Ряд сходится (расходится) тогда и только тогда, когда сходится (расходится) несобственный интеграл 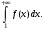
Задания 9.1 – 9.2. Знакопеременный числовой ряд
 называется абсолютно сходящимся, если сходится ряд
называется абсолютно сходящимся, если сходится ряд 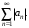
Абсолютно сходящийся ряд сходится.
Знакопеременный ряд называется условно сходящимся, если он сходится, но не абсолютно.
Знакопеременный ряд называется знакочередующимся, если любые два его соседних члена имеют разные знаки:
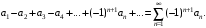
где
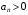
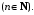
Признак Лейбница. Если для знакочередующегося ряда
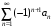
выполняются условия:
1)
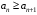 (начиная с некоторого номера
(начиная с некоторого номера  );
);2)
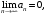
то ряд сходится, а его сумма
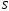 удовлетворяет условию
удовлетворяет условию 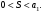
Следствие признака Лейбница. Если
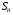 – n-я частичная сумма знакочередующегося ряда
– n-я частичная сумма знакочередующегося ряда 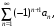 то
то 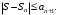
Степенным рядом называется ряд вида
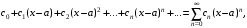
где
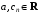
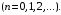
Радиусом сходимости степенного ряда называется число r, которое находят по формуле
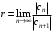 или
или 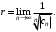
Ряд
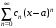 сходится, причем абсолютно, на интервале сходимости
сходится, причем абсолютно, на интервале сходимости 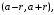 где
где 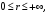 и расходится на
и расходится на 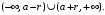
Для определения области сходимости степенного ряда следует:
1) найти его радиус сходимости;
2) определить интервал сходимости с центром в точке a;
3) выяснить вопрос о сходимости ряда в граничных точках этого интервала, подставив их вместо x в заданный ряд.
Задания 10.1 – 10.2. Пусть требуется вычислить значение функции
 при
при 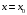 с заданной точностью
с заданной точностью  и функцию
и функцию  можно разложить в степенной ряд
можно разложить в степенной ряд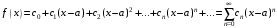
в интервале
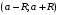 и
и 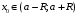
.Тогда
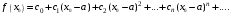
Взяв достаточное число членов ряда, получим приближенное равенство
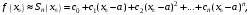
точность которого увеличивается с возрастанием
 .
. Для того чтобы вычислить значение функции
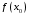 с точностью
с точностью 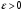 ,
, необходимо взять сумму такого количества
 первых членов ряда, чтобы
первых членов ряда, чтобы 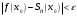 .
.Степенной ряд вида
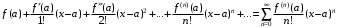
называется рядом Тейлора функции
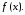
Рядом Маклорена функции
 называется ряд Тейлора вида
называется ряд Тейлора вида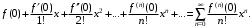
Имеют место разложения элементарных функций в ряд Маклорена:
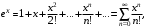
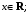
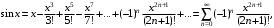
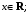
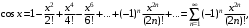
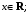
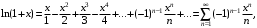
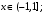
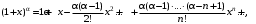
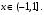
4. Методические рекомендации к выполнению
контрольной работы
Задание 1. Найти неопределенные интегралы:
а)
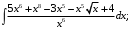 б)
б) 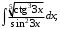 в)
в) 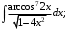
Решение. а) Преобразуем подынтегральное выражение, а затем используем правила интегрирования и формулы (3), (4) таблицы интегралов:
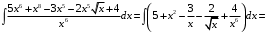
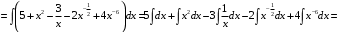
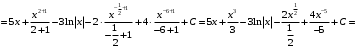
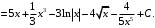
б) 1-й способ. Выполним подстановку
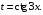 Тогда
Тогда 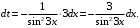
Получим
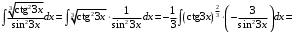
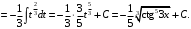
2-й способ. Применим метод поднесения под знак дифференциала. Так как
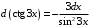 , то
, то 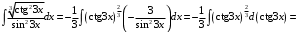
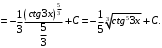
в) 1-й способ. Применим подстановку
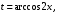 тогда
тогда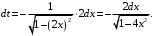 Получим
Получим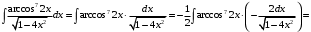
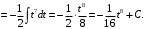
Перейдя к переменной
 , получим
, получим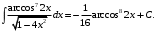
2-й способ. Применим метод поднесения под знак дифференциала. Так как
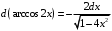 , то
, то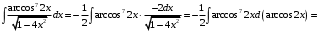
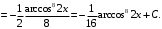
Задание 2. Вычислить определенные интегралы:
а)
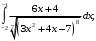 б)
б) 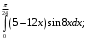
в)
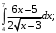
Решение. а) Применим метод поднесения под знак дифференциала. Поскольку
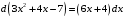 , то
, то 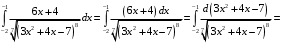
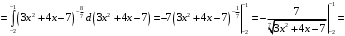
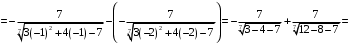
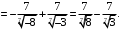
б) Применим формулу (2) интегрирования по частям для определенного интеграла:
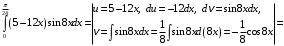
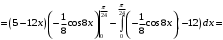
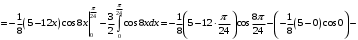
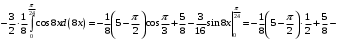
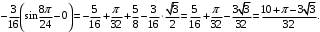
в) Заменяем
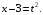 Тогда
Тогда 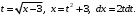 Определим новые пределы интегрирования. Если
Определим новые пределы интегрирования. Если 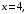 то
то 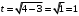 . Если
. Если 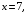 то
то 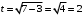 . Следовательно,
. Следовательно,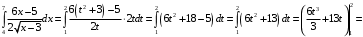
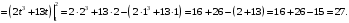
Задание 3. Вычислить несобственный интеграл первого рода:
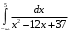 ;
;Решение. 1) По определению несобственного интеграла имеем
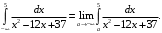
Выделим в знаменателе подынтегрального выражения полный квадрат и получим
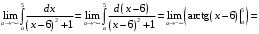
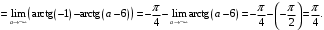
Задание 4. Вычислить площадь фигуры, ограниченной заданными линиями. Сделать рисунок.
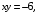
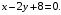
Решение. Искомая фигура изображена на (рис. 5).
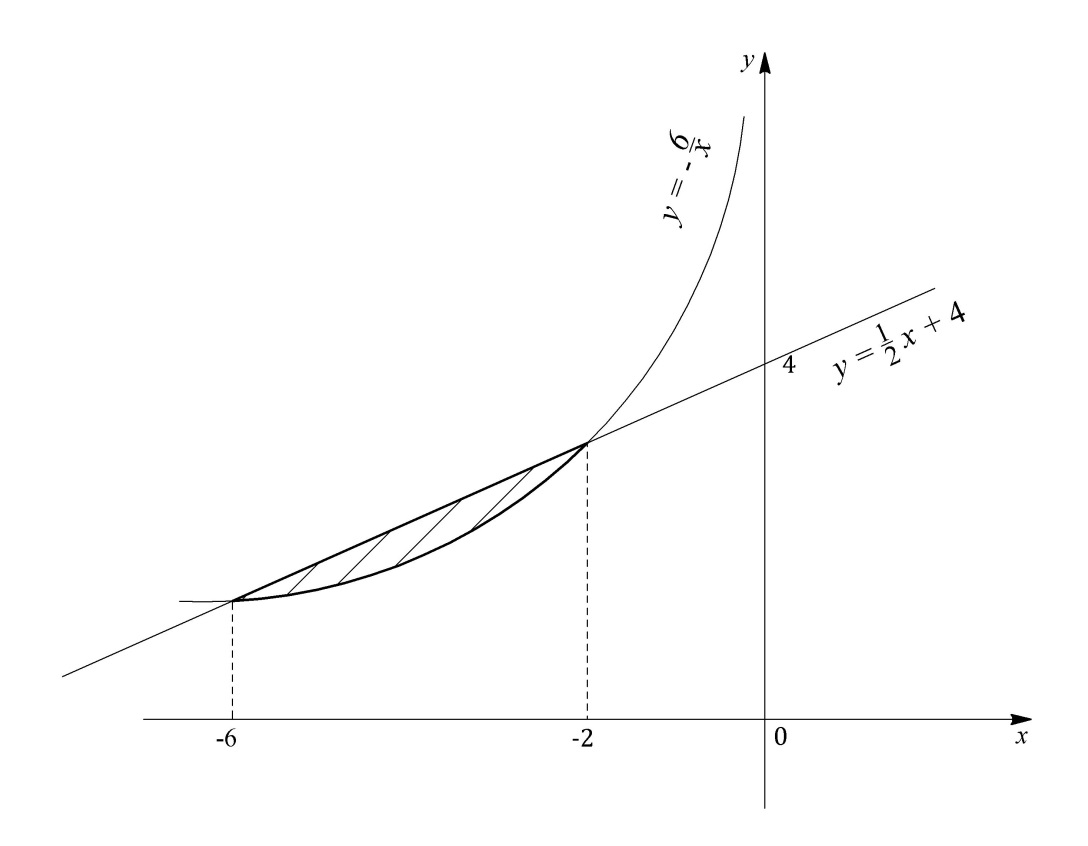
Рис. 5
Найдем точки пересечения данных кривых. Для этого решим систему уравнений: