Файл: Рекомендации по выполнению контрольной работы по дисциплине Математический анализ.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 06.11.2023
Просмотров: 53
Скачиваний: 2
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
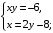
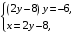
откуда
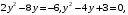 т. е.
т. е. 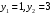 . Тогда
. Тогда 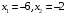 .
.Площадь данной фигуры, ограниченной линиями
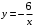 и
и 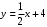 , находим по формуле (3).
, находим по формуле (3).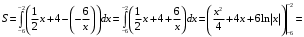
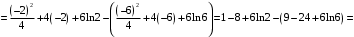
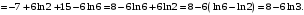
Задание 5. Найти общие решения дифференциальных уравнений:
а)
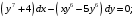 б)
б) 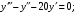
в)
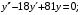 г)
г) 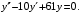
Решение. а) Это дифференциальное уравнение с разделяющимися переменными.
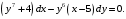
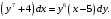
Разделим обе части уравнения на
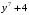 и на
и на 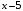 при условии
при условии 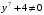 и
и 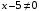 :
: 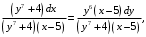
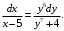
Теперь переменные разделены. Интегрируем обе части уравнения:
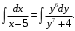
Вычислим второй интеграл используя метод поднесения под знак дифференциала. Поскольку
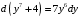 , то
, то 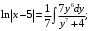
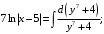
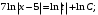
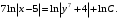
Произвольную константу записали в форме
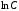 (где
(где 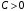
), чтобы в итоге получить решение в удобной форме записи.
Применим свойства логарифма
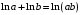 и
и 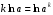 . Получим
. Получим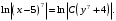
Отсюда общее решение запишется в виде
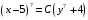 , где
, где 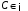 .
.б) Это линейное однородное дифференциальное уравнение с постоянными коэффициентами. Его характеристическое уравнение имеет вид
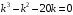 , найдем корни. Разлагаем левую часть этого уравнения на множители
, найдем корни. Разлагаем левую часть этого уравнения на множители 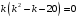 . Тогда
. Тогда 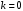 или
или 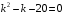 . Получили корни характеристического уравнения:
. Получили корни характеристического уравнения: 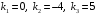 . Все корни различные вещественные числа. Частными решениями дифференциального уравнения, соответствующими полученным корням характеристического уравнения, на основании (4, будут
. Все корни различные вещественные числа. Частными решениями дифференциального уравнения, соответствующими полученным корням характеристического уравнения, на основании (4, будут 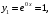
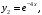
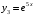 . Общее решение принимает вид
. Общее решение принимает вид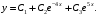
в) Составим характеристическое уравнение
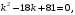
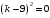 . Поэтому
. Поэтому 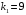 ,
, 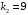 . Корни вещественны и равны, т. е.
. Корни вещественны и равны, т. е. 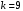 корень кратности 2. Частными решениями дифференциального уравнения, на основании (5), будут
корень кратности 2. Частными решениями дифференциального уравнения, на основании (5), будут 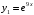 ,
, 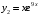 , а общее решение запишется в виде
, а общее решение запишется в виде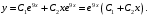
г) Запишем характеристическое уравнение
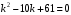 . Решаем его как квадратное:
. Решаем его как квадратное: 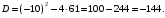
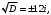
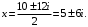 Получили два комплексно сопряженных корня вида
Получили два комплексно сопряженных корня вида 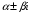 , где
, где 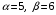 . Тогда частными решениями данного уравнения, на основании (6), будут
. Тогда частными решениями данного уравнения, на основании (6), будут 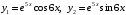 . Общее решение принимает вид
. Общее решение принимает вид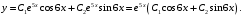
Задание 6. Решить задачу Коши при начальном условии

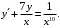
Решение. Данное уравнение является линейным дифференциальным уравнением первого порядка, так как искомая функция
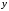 и ее производная
и ее производная 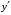 входят в него в первой степени. Решим его методом Бернулли. Общее решение уравнения будем искать в виде
входят в него в первой степени. Решим его методом Бернулли. Общее решение уравнения будем искать в виде 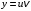 , где
, где 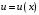 и
и 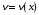 – дифференцируемые функции. Находим
– дифференцируемые функции. Находим 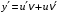 . Подставим
. Подставим 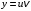 и
и 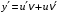 в заданное уравнение:
в заданное уравнение: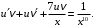
Сгруппируем второе и третье слагаемые и вынесем за скобки общий множитель
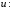
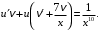
Согласно используемому методу решения находим функцию
 как частное решение дифференциального уравнения
как частное решение дифференциального уравнения 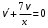 . Последнее уравнение решаем как дифференциальное уравнение с разделяющимися переменными. Получаем
. Последнее уравнение решаем как дифференциальное уравнение с разделяющимися переменными. Получаем 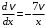 , откуда
, откуда 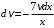 . Разделим обе части уравнения на
. Разделим обе части уравнения на  и получим
и получим 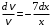 ( при условии
( при условии 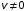 ). Почленно интегрируя, имеем
). Почленно интегрируя, имеем
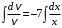 ,
, 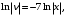
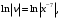
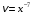 ,
, 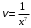 .
.В итоге для определения функции
 имеем уравнение
имеем уравнение 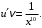 Подставим в него найденную функцию
Подставим в него найденную функцию  и снова получаем дифференциальное уравнение с разделяющимися переменными:
и снова получаем дифференциальное уравнение с разделяющимися переменными: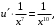
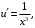
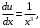
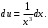
Интегрируем и получаем
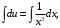
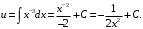
Запишем общее решение
 для найденных функций
для найденных функций  и
и  :
: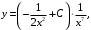
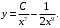
Используя начальное условие
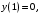 подставляем в общее решение заданные значения переменных
подставляем в общее решение заданные значения переменных 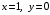 и определяем соответствующее значение произвольной постоянной
и определяем соответствующее значение произвольной постоянной 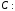
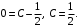 При этом значении
При этом значении 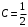 из общего решения получаем частное решение задачи Коши
из общего решения получаем частное решение задачи Коши 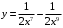 , удовлетворяющее заданному начальному условию.
, удовлетворяющее заданному начальному условию.Задание 7. Изобразить заданное тело и его проекцию на плоскость
 С помощью двойного интеграла вычислить объем тела, ограниченного указанными поверхностями.
С помощью двойного интеграла вычислить объем тела, ограниченного указанными поверхностями. а)
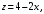


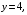
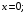
б)
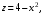

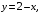
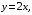
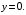
Решение. а) Данное тело (рис. 6) ограничено сверху частью плоскости
 а боковая поверхность образована в результате пересечения параболического цилиндра
а боковая поверхность образована в результате пересечения параболического цилиндра 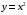 , плоскости
, плоскости 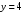 и плоскости
и плоскости 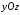
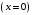 .
. 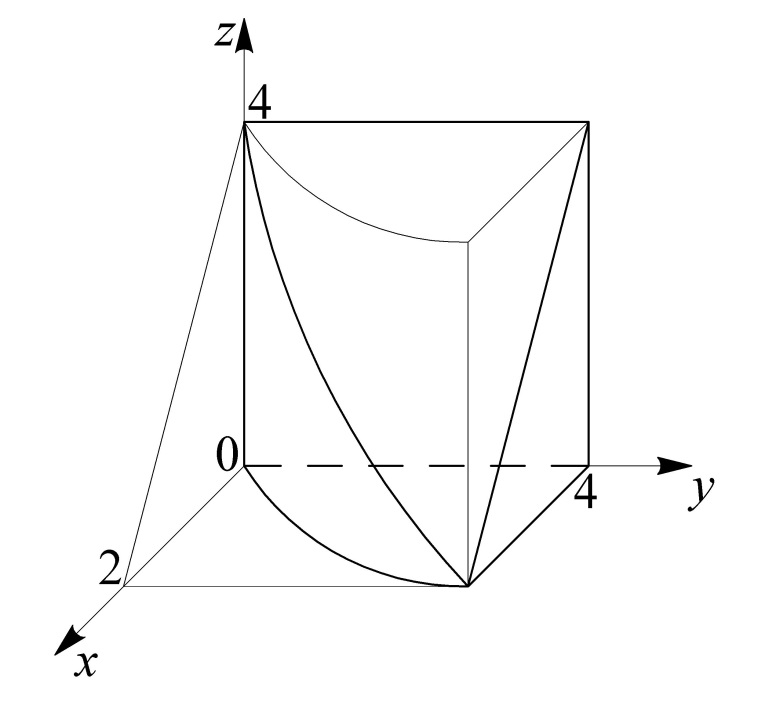
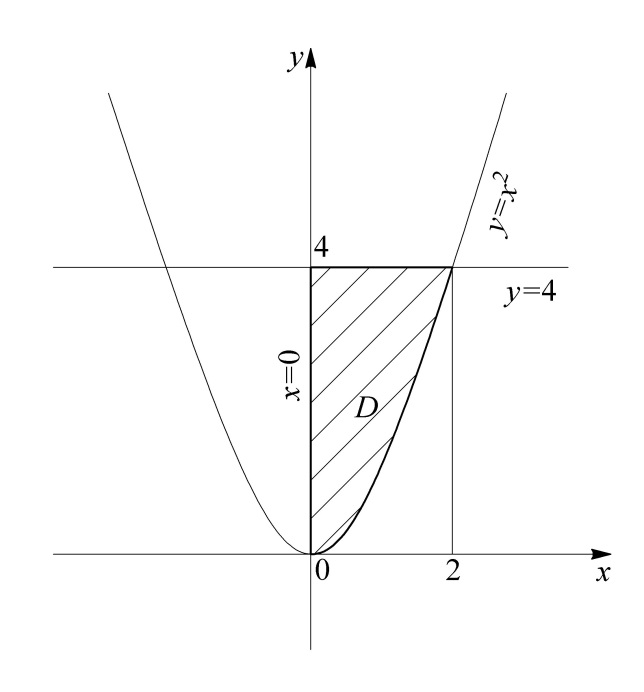
Рис. 6 Рис. 7
Область
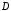 (проекция тела на плоскость
(проекция тела на плоскость 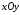 ) ограничена параболой
) ограничена параболой  прямыми
прямыми 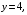
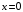 (рис. 7). Область
(рис. 7). Область 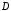 ограничивает тело снизу. Область
ограничивает тело снизу. Область 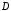 является правильной в отношении оси
является правильной в отношении оси  .
. Объем тела вычисляется по формуле (7):
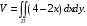
Решая совместно уравнения
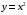 и
и 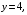 находим координаты точки пересечения параболы и прямой:
находим координаты точки пересечения параболы и прямой: 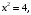
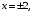
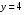 . Переходим к повторному (двукратному) интегралу и выполняем внутреннее интегрирование по
. Переходим к повторному (двукратному) интегралу и выполняем внутреннее интегрирование по 