Файл: Дана Система Линейных Алгебраических Уравнений. Требуется решить её тремя способами 1) Решить её методом Гаусса (исключения неизвестных элементарными преобразованиями матрицы) Проверить решение.doc
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 08.11.2023
Просмотров: 69
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
СОДЕРЖАНИЕ
Задание «Решение СЛАУ»
Оглавление
Условие задания 1
Примеры решения СЛАУ. 4
1. ПРИМЕР Решения СЛАУ методом Гаусса (исключения неизвестных элементарными преобразованиями расширенной матрицы системы). 4
2. Пример решения СЛАУ «матричным методом» (с использованием обратной матрицы). Вычисление обратной матрицы методом Жордана-Гаусса. 8
3. Пример Решения СЛАУ методом Крамера 12
Условие задания
Дана Система Линейных Алгебраических Уравнений. Требуется решить её тремя способами:
1) Решить её методом Гаусса (исключения неизвестных элементарными преобразованиями матрицы); Проверить решение подстановкой в исходную систему.
2) Решить её методом Крамера (с помощью главного и вспомогательных определителей);
3) Вычислить для матрицы системы обратную матрицу методом Жордана-Гаусса, умножить обратную матрицу на столбец правых частей. Проверить, что получилось решение системы.
(«Решить СЛАУ матричным методом»).
1.
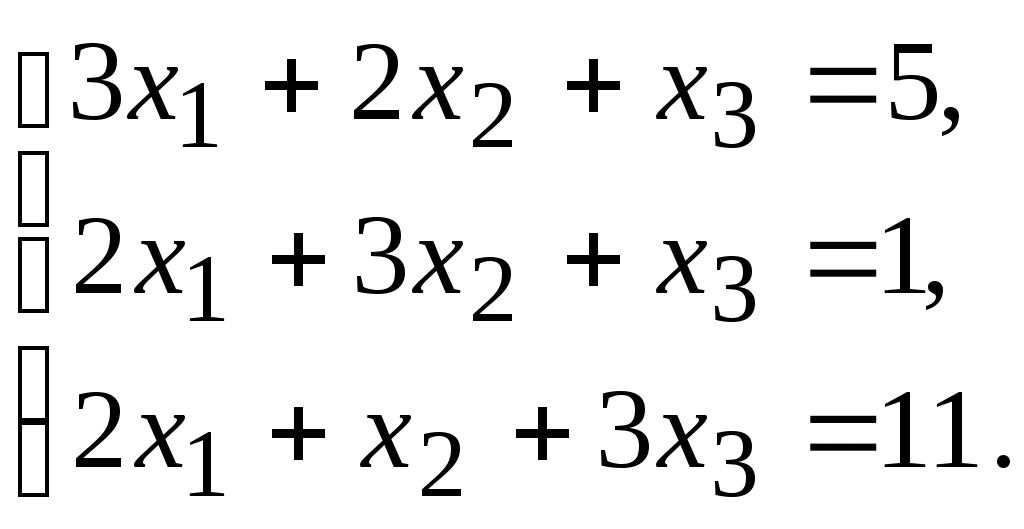 2.
2. 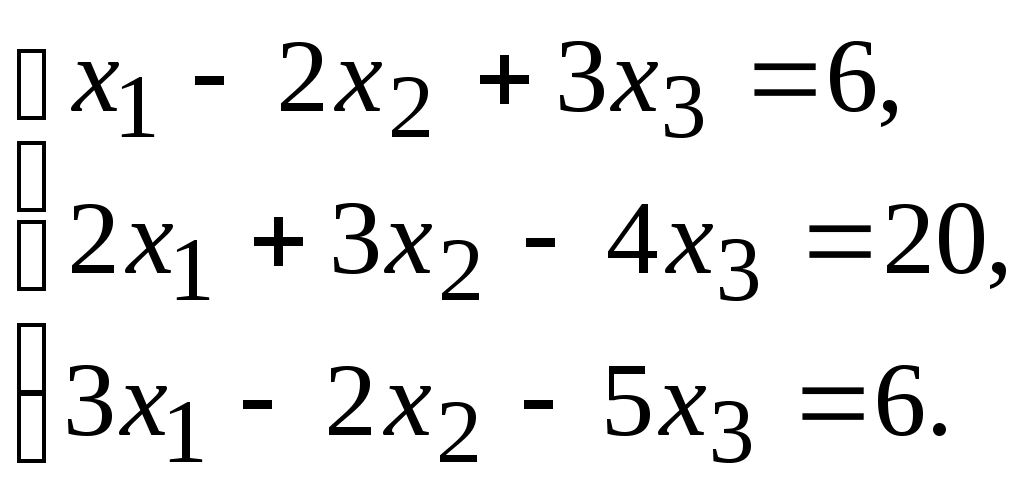
3.
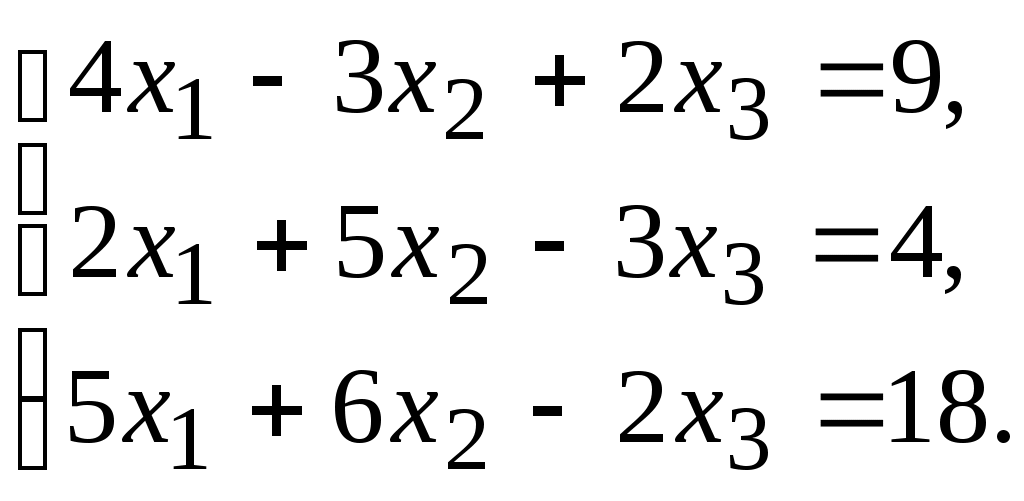 4.
4. 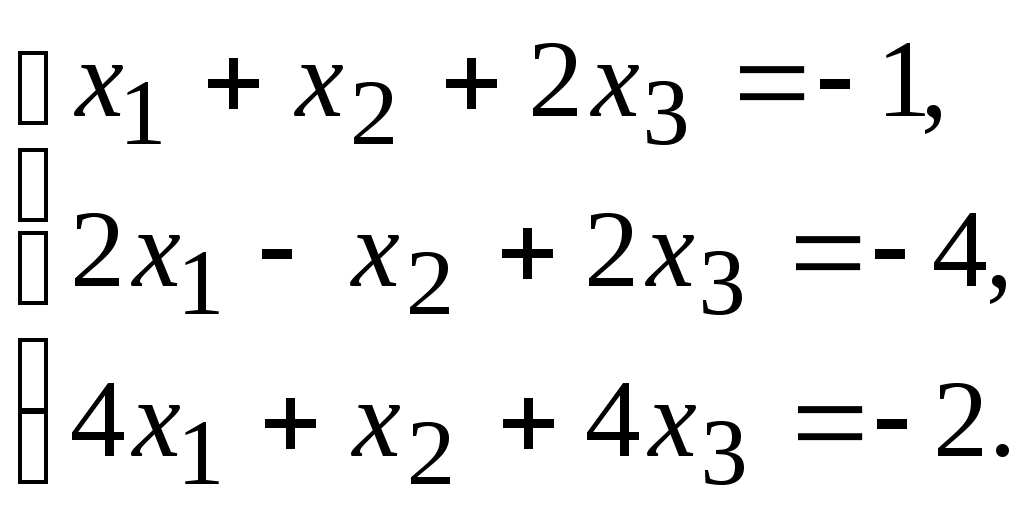
5.
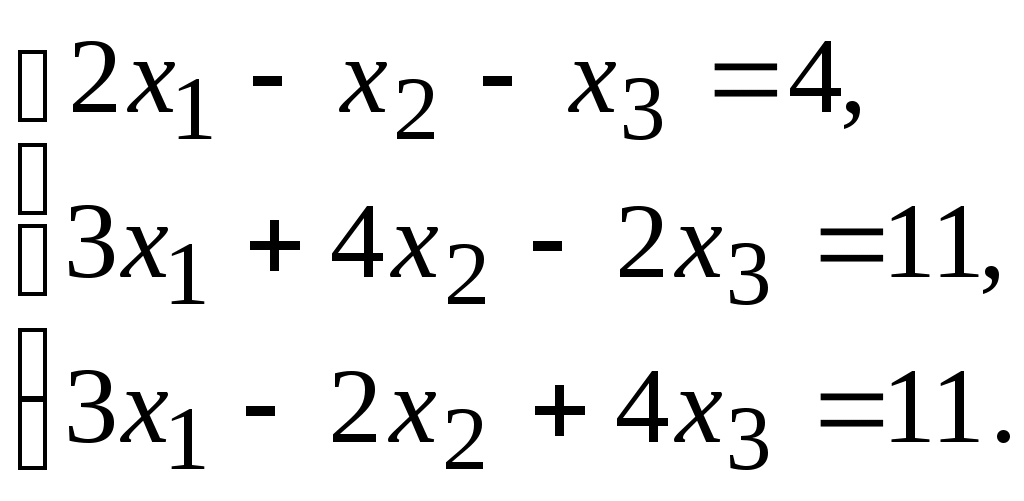 6.
6. 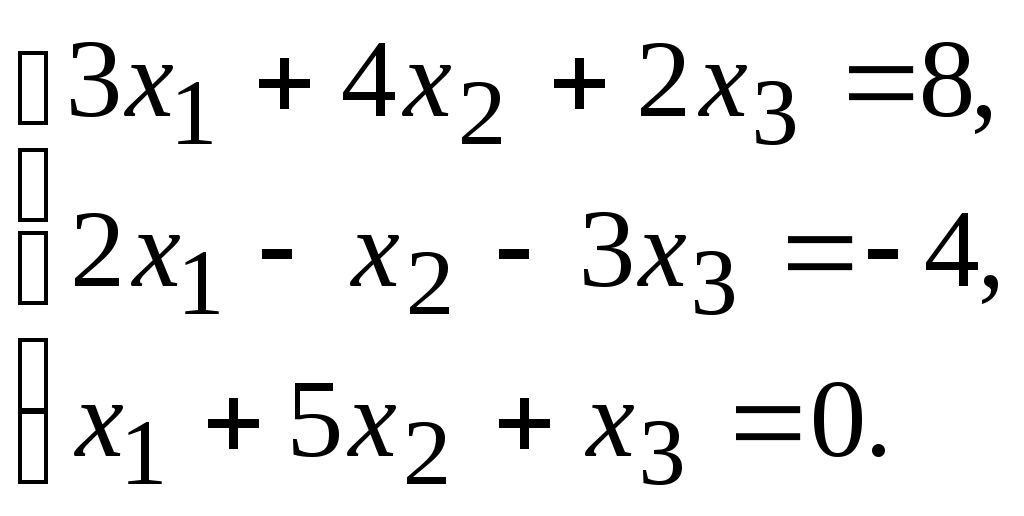
7.
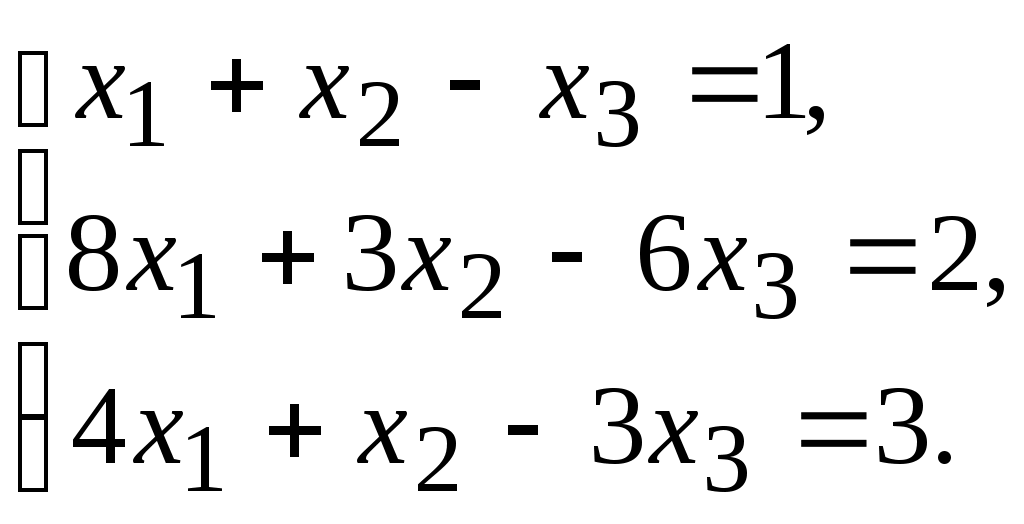 8.
8. 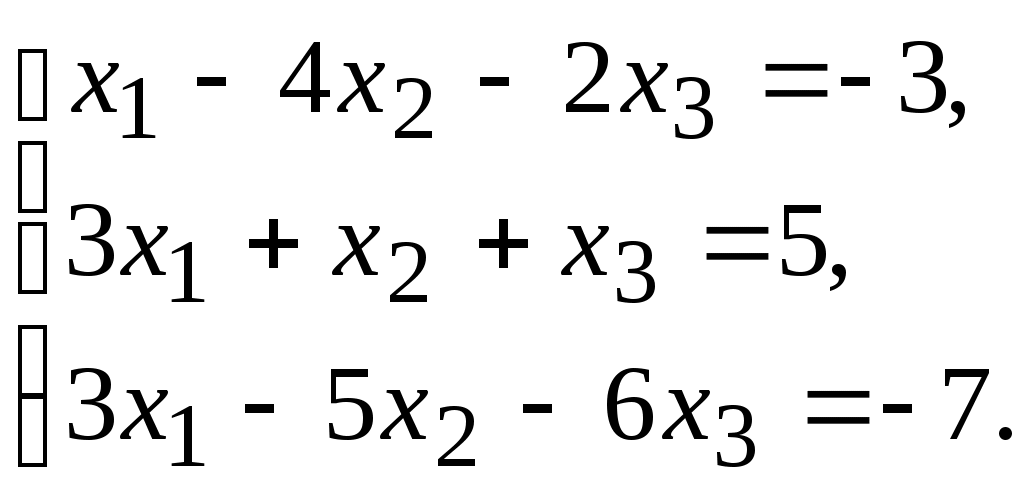
9.
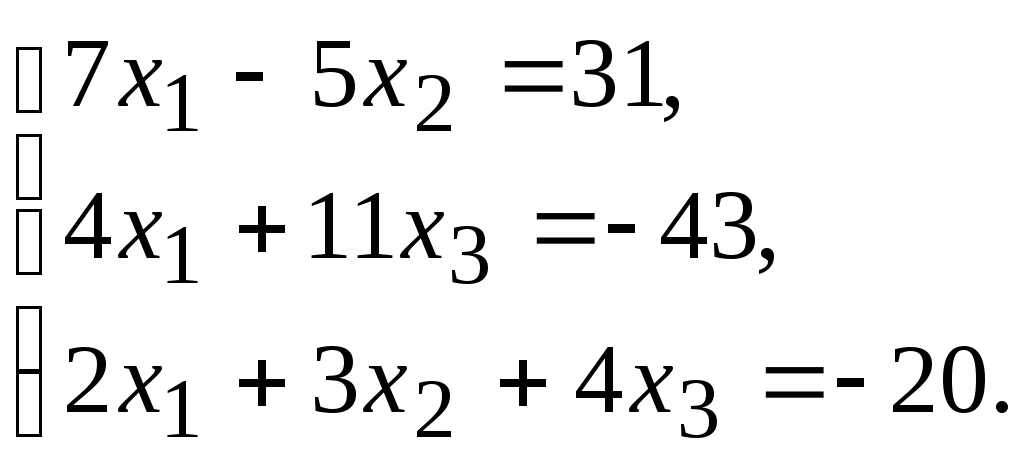 10.
10. 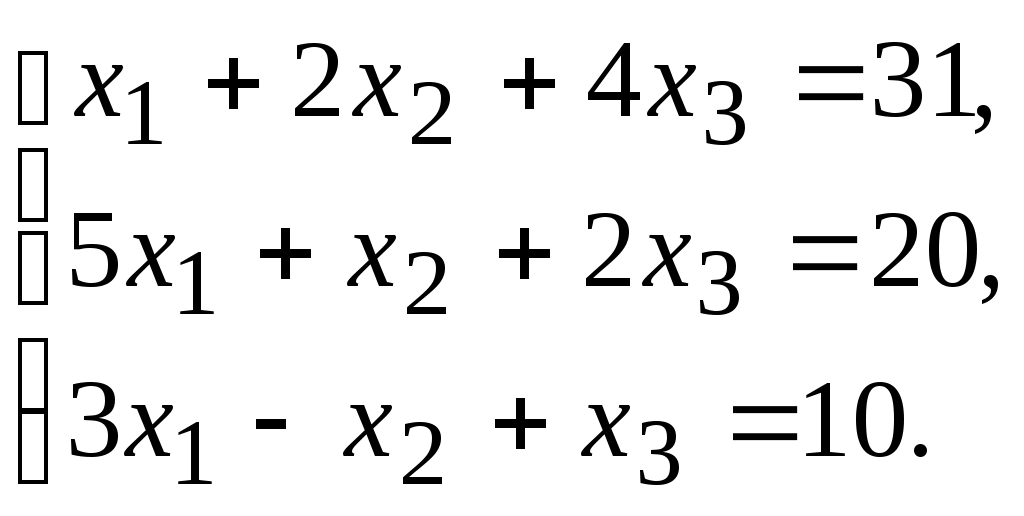
11.
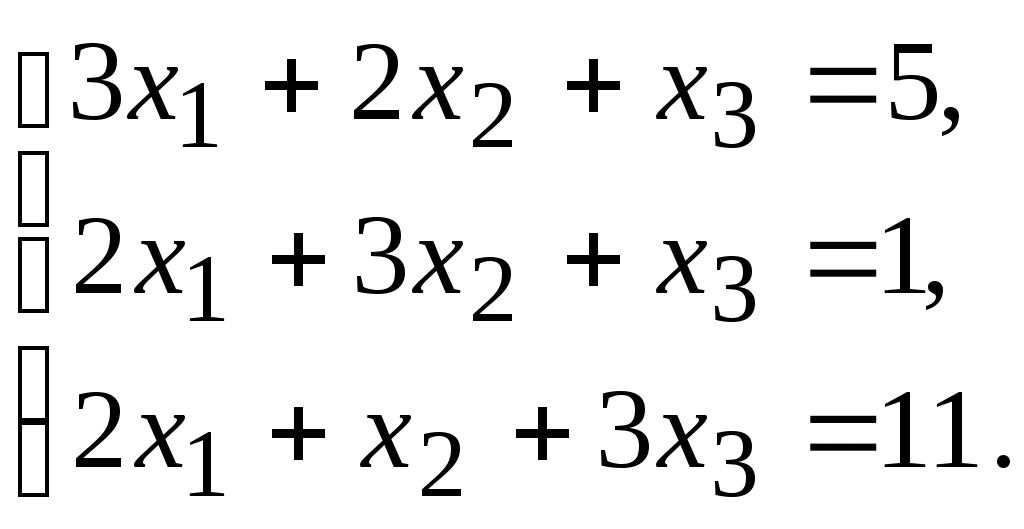 12.
12. 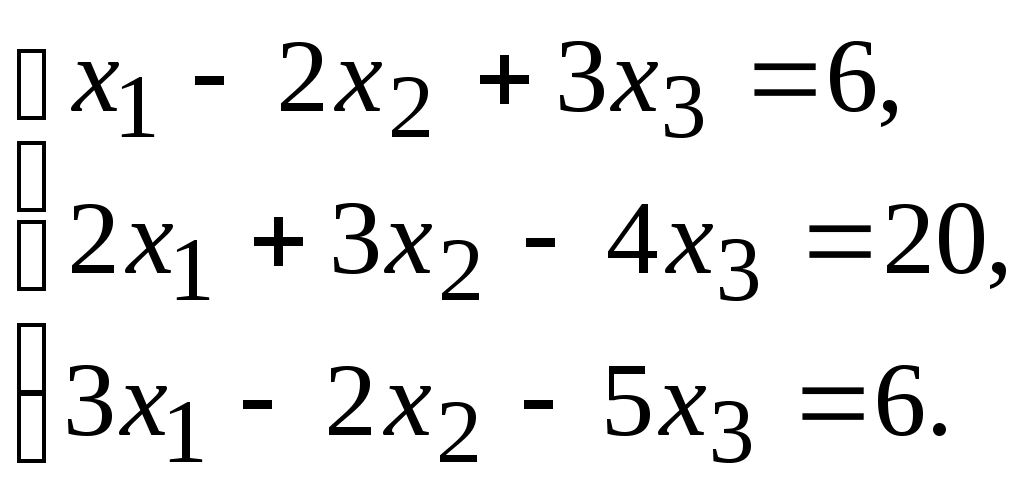
13.
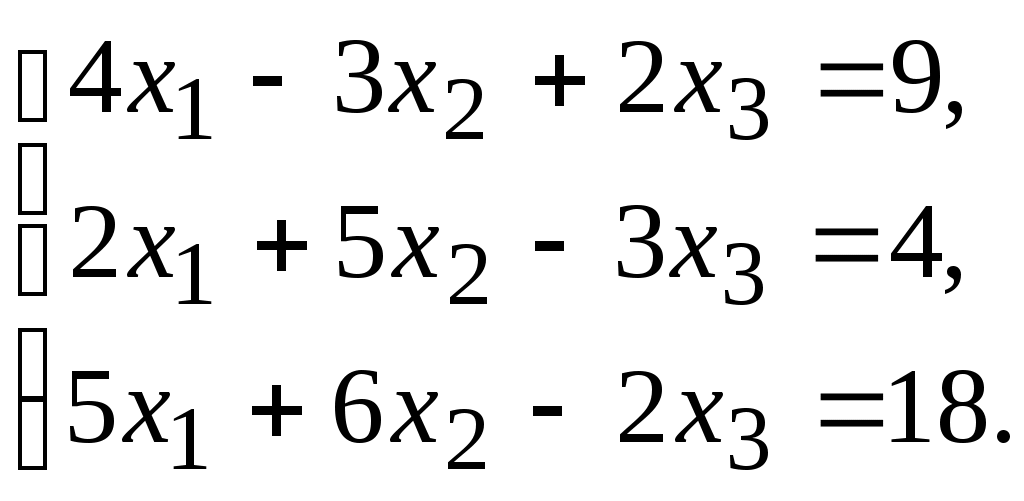 14.
14. 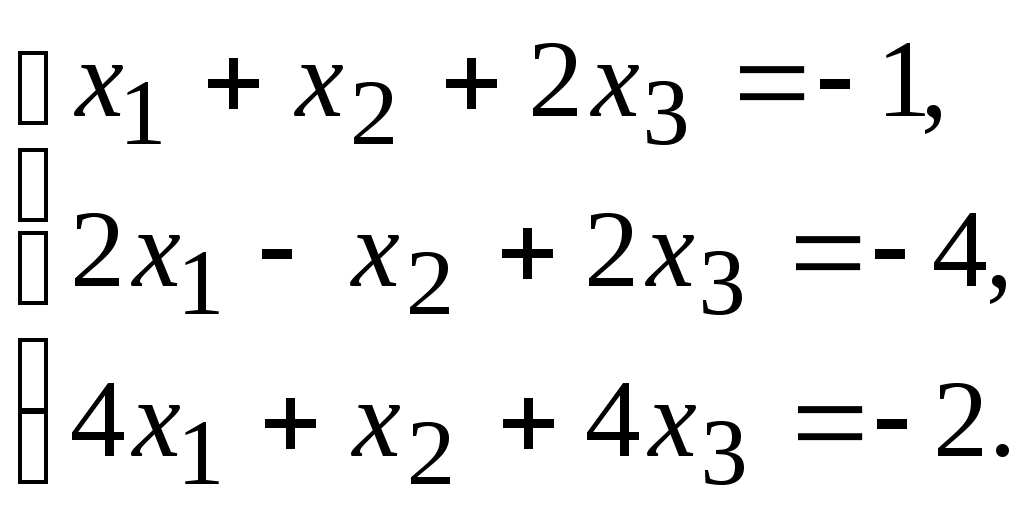
15.
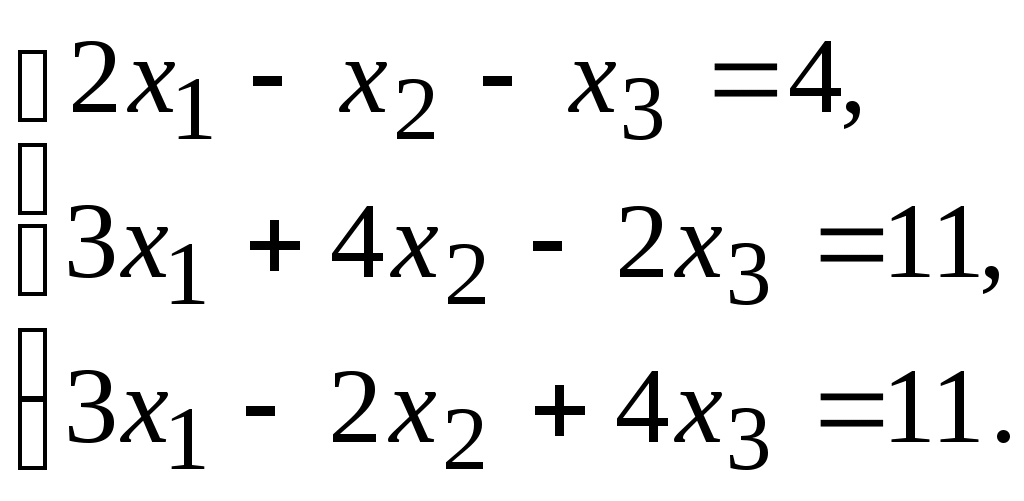
16.

17.
 18.
18. 
19.
 20.
20. 
21.
 22.
22. 
23.
 24.
24. 
25.
 26.
26. 
27.
 28.
28. 
29.
 30.
30. 
Примеры решения СЛАУ.
Дана система уравнений
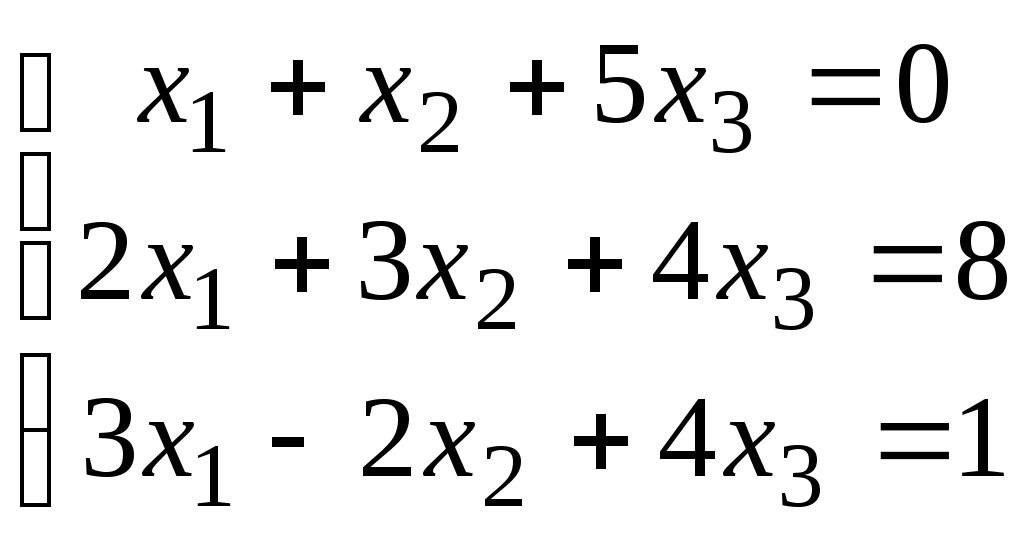
1. ПРИМЕР Решения СЛАУ методом Гаусса (исключения неизвестных элементарными преобразованиями расширенной матрицы системы).
Метод Гаусса – это метод последовательного исключения неизвестных.
Суть метода применительно к системе
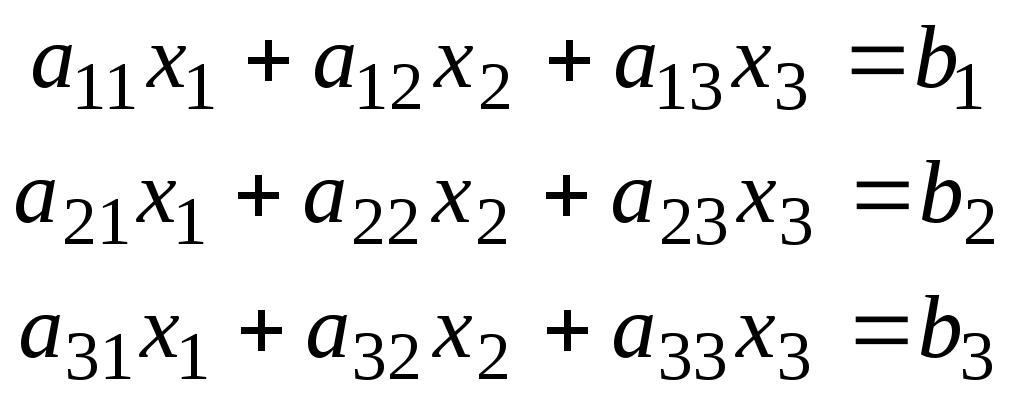
состоит в поочередном исключении неизвестных из уравнений, «перебираемых сверху вниз», а затем в вычислении переменных «снизу вверх»:
1. Прямой ход метода Гаусса
Переменная
Полученное выражение для x1 подставляется во 2-е и 3-е уравнения вместо
Таким образом переменная
Переменная x2 выражается из 2-го уравнения через переменную x3;
Полученное выражение для x2 подставляется в 3-е уравнения вместо x2.
Таким образом переменная x2 исключается из 3-го уравнения.
В результате система преобразуется в равносильную ей систему треугольного вида
(с другими коэффициентами и правыми частями, но с теми же решениями):
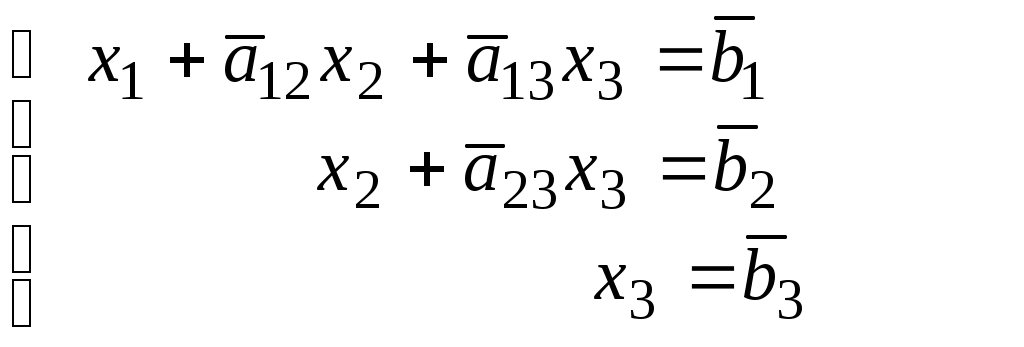
2. Обратный ход метода Гаусса.
Значения неизвестных вычисляются из системы треугольного вида при «движении снизу вверх»:
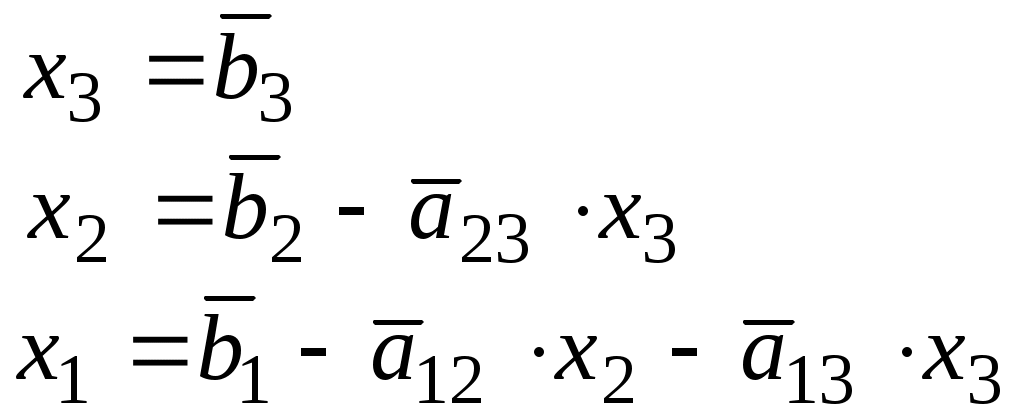 .
.При решении систем линейных уравнений удобно работать не с самой системой, а с ее расширенной матрицей. Исключение неизвестных «на языке матриц» проводится с помощью т.н. элементарных преобразований матриц.
В методе Гаусса в основном применяется следующее элементарное преобразование:
(1) Прибавление к одной строке матрицы другой строки, умноженной на число; (соответствует прибавлению к одному уравнению системы другого).
Это преобразование используется для «зануления» нужного элемента строки.
Иногда необходимо преобразование
(2) Перестановка строк матрицы (соответствует перестановке уравнений в системе).
Это преобразование используется, чтобы на нужное место строки поставить ненулевой элемент.
Далее в примере решения СЛАУ используется преобразование (1) – сложение строк.
| Рассмотрим СЛАУ |
|
Выпишем матрицу коэффициентов СЛАУ, столбец правых частей и столбец неизвестных:
(матрицы и столбцы ниже заключены в квадратные скобки)
| A = |
| , | b = |
| , | x = |
| , |
| Расширенная матрица СЛАУ такова: |
|
Применим к матрице следующие элементарные преобразования:
Прибавим ко 2-й строке 1-ю строку, умноженную на -2;
прибавим к 3-й строке 1-ю строку, умноженную на -3
(первая строка не меняется):
| ≡ |
|
Говоря на языке уравнений мы исключили первую переменную из уравнений 2 и 3.
| Соответствующая система уравнений выглядит так: |
|
В системе появилась подсистема из 2-х уравнений №2 и 3 с двумя неизвестными x2 и x3.
Применим к получившейся матрице элементарное преобразование:
прибавим к 3-й строке 2-ю строку, умноженную на 5:
(первая и вторая строка не меняется):
| ≡ |
|
Говоря на языке уравнений мы исключили вторую переменную из уравнения 3.
Преобразованной матрице соответствует преобразованная СЛАУ:
1*x1 + 1*x2 + 5*x3 = 0
0*x1 + 1*x2 + (-6)*x3 = 8
0*x1 + 0*x2 + (-41)*x3 = 41
или
x 1 + x2 + 5x3 = 0
x2 – 6x3 = 8
– 41 x3 = 41
Выполним обратный ход метода Гаусса для определения значений неизвестных из уравнений «снизу вверх»:
x 3 = 41/(-41) = –1
x 2 = 8 + 6x 3 = 8 + 6*(– 1) = 8 – 6 = 2
x 1 = 0 – x 2 – 5x 3 = –2 – 5(–1) = –2 + 5 = 3
| Можно записать вектор решения: | x = |
| = |
| . |