ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 08.11.2023
Просмотров: 152
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
СОДЕРЖАНИЕ
2. ОПРЕДЕЛЕНИЕ КОЭФФИЦИЕНТА ПОВЕРХНОСТНОГО НАТЯЖЕНИЯ.
3. ОПРЕДЕЛЕНИЕ КОЭФФИЦИЕНТА ЛИНЕЙНОГО РАСШИРЕНИЯ МЕТАЛЛОВ
4. ОПРЕДЕЛЕНИЕ УДЕЛЬНОЙ ТЕПЛОЕМКОСТИ ТВЕРДЫХ ТЕЛ.
5. ОПРЕДЕЛЕНИЕ КОЭФФИЦИЕНТА ВЯЗКОСТИ ГАЗОВ И СРЕДНЕЙ ДЛИНЫ ПРОБЕГА МОЛЕКУЛ.
6. ОПРЕДЕЛЕНИЕ ПОКАЗАТЕЛЯ АДИАБАТЫ ДЛЯ ВОЗДУХА МЕТОДОМ КЛЕМАНА-ДЕЗОРМА.
5. ОПРЕДЕЛЕНИЕ КОЭФФИЦИЕНТА ВЯЗКОСТИ ГАЗОВ И СРЕДНЕЙ ДЛИНЫ ПРОБЕГА МОЛЕКУЛ.
ЦЕЛИ РАБОТЫ:
-
Ознакомиться с явлением вязкости и теоретическими представлениями о механизме возникновения сил вязкого трения. -
Изучить особенности протекания жидкостей и газов по трубам. -
Освоить метод капиллярного вискозиметра для измерения вязкости газа.
ПРИБОРЫ И ПРИНАДЛЕЖНОСТИ:
-
Капилляр; -
Манометр; -
Аспиратор; -
Секундомер; -
Миллиметровая линейка; -
Мензурка.
КРАТКАЯ ТЕОРИЯ
Явления вязкости, теплопроводности, диффузии относятся к явлениям переноса. Они возникают в термодинамических системах при отклонении их от равновесного состояния. Так, если создать разность температур в различных областях объема газа, то возникнет поток тепла, стремящейся восстановить равновесие. Это явление переноса тепла в неравновесной термодинамической системе называется теплопроводностью.
При перемещении одного слоя жидкости относительно другого между слоями жидкости возникают силы, стремящиеся затормозить это движение. Это явление называют внутренним трением, или вязкостью. Закон, описывающий силы внутреннего трения, был установлен экспериментально Исааком Ньютоном и носит его имя. Поскольку жидкость «прилипает» к поверхности твердых тел, то для изучения внутреннего трения между слоями жидкостями можно рассмотреть два параллельных плоских тела площадью
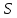 каждое, одно из которых движется относительно другого со скоростью
каждое, одно из которых движется относительно другого со скоростью  и находится на малом расстоянии h от другого. Если пространство между телами заполнено жидкостью, то на движущееся тело действует сила трения, примерно равная
и находится на малом расстоянии h от другого. Если пространство между телами заполнено жидкостью, то на движущееся тело действует сила трения, примерно равная , (5.1)
, (5.1) Коэффициент пропорциональности
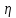 , зависящий от природы жидкости или газа, называют коэффициентом динамической вязкости.
, зависящий от природы жидкости или газа, называют коэффициентом динамической вязкости.
Рисунок 10.
Полученный закон можно сформулировать и точно. Для этого рассмотрим жидкость
, текущую вдоль оси
 , причем скорость течения зависит от координаты
, причем скорость течения зависит от координаты 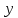 (см. Рис. 10). Выберем два слоя со скоростями
(см. Рис. 10). Выберем два слоя со скоростями  и
и 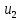 с разностью скоростей
с разностью скоростей 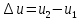 . Предел отношения
. Предел отношения 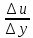 при
при 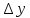 , стремящемся к нулю, называется градиентом скорости и показывает быстроту изменения скорости при переходе от слоя к слою в перпендикулярном скорости направлении. Этот предел обозначается как
, стремящемся к нулю, называется градиентом скорости и показывает быстроту изменения скорости при переходе от слоя к слою в перпендикулярном скорости направлении. Этот предел обозначается как 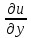 . Силу внутреннего трения, действующую на слой, согласно закону Ньютона, можно записать как
. Силу внутреннего трения, действующую на слой, согласно закону Ньютона, можно записать как , (5.2)
, (5.2) Сила
 направлена по касательной к границе разделов слоев. Единицы измерения коэффициента динамической вязкости η в Международной системе единиц (СИ) — паскаль·секунда (Па·с), в системе СГС — Пуаз (П). При этом 1 Па·с = 10 П.
направлена по касательной к границе разделов слоев. Единицы измерения коэффициента динамической вязкости η в Международной системе единиц (СИ) — паскаль·секунда (Па·с), в системе СГС — Пуаз (П). При этом 1 Па·с = 10 П.Закон вязкости Ньютона справедлив не только для жидкостей, но и для газов. Для газов теория внутреннего трения относительно проста. В газах основным фактором является перенос импульса вместе с молекулами из одного слоя в другой. В результате медленный слой обогащается быстрыми молекулами и ускоряется, а быстрый слой обедняется быстрыми молекулами и замедляется.
Молекулярно-кинетическая теория газов, с учетом распределения Максвелла молекул по скоростям, дает следующее выражение для коэффициента вязкости:
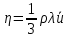 , (5.3)
, (5.3) где ρ - плотность газа,
 - средняя длина свободного пробега молекул,
- средняя длина свободного пробега молекул, 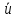 - средняя арифметическая скорость движения молекул. Распределение Максвелла дает
- средняя арифметическая скорость движения молекул. Распределение Максвелла дает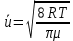 , (5.4)
, (5.4) где
 - универсальная газовая универсальная, а
- универсальная газовая универсальная, а
 - молярная масса газа.
- молярная масса газа.Если значение коэффициента динамической вязкости
 известно из опыта, то из двух формул выше можно выразить
известно из опыта, то из двух формул выше можно выразить  :
: , (5.5)
, (5.5) Плотность идеального газа выражается из уравнения Менделеева-Клапейрона
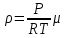 , (5.6)
, (5.6) где
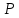 - атмосферное давление. Подстановка этого выражения приводит к
- атмосферное давление. Подстановка этого выражения приводит к  . (5.7)
. (5.7) Молекулярно-кинетическая теория газов также позволяет связать среднюю длину свободного пробега
 с эффективным диаметром молекул
с эффективным диаметром молекул 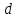 :
: , (5.8)
, (5.8) где
 - постоянная Больцмана. С учетом этого эффективный диаметр молекул газа можно определить по формуле
- постоянная Больцмана. С учетом этого эффективный диаметр молекул газа можно определить по формуле . (5.9)
. (5.9) ТЕОРИЯ МЕТОДА КАПИЛЛЯРНОГО ВИСКОЗИМЕТРА
Рассмотрим движение газа (или вязкой жидкости) по трубе круглого сечения в направлении оси
 . При достаточно малых скоростях потока движение оказывается ламинарным (слоистым). Скорости направленного движения частиц газа медленно изменяются в сечении трубы (на рисунке - вдоль оси
. При достаточно малых скоростях потока движение оказывается ламинарным (слоистым). Скорости направленного движения частиц газа медленно изменяются в сечении трубы (на рисунке - вдоль оси  ) и параллельны оси
) и параллельны оси  .
. 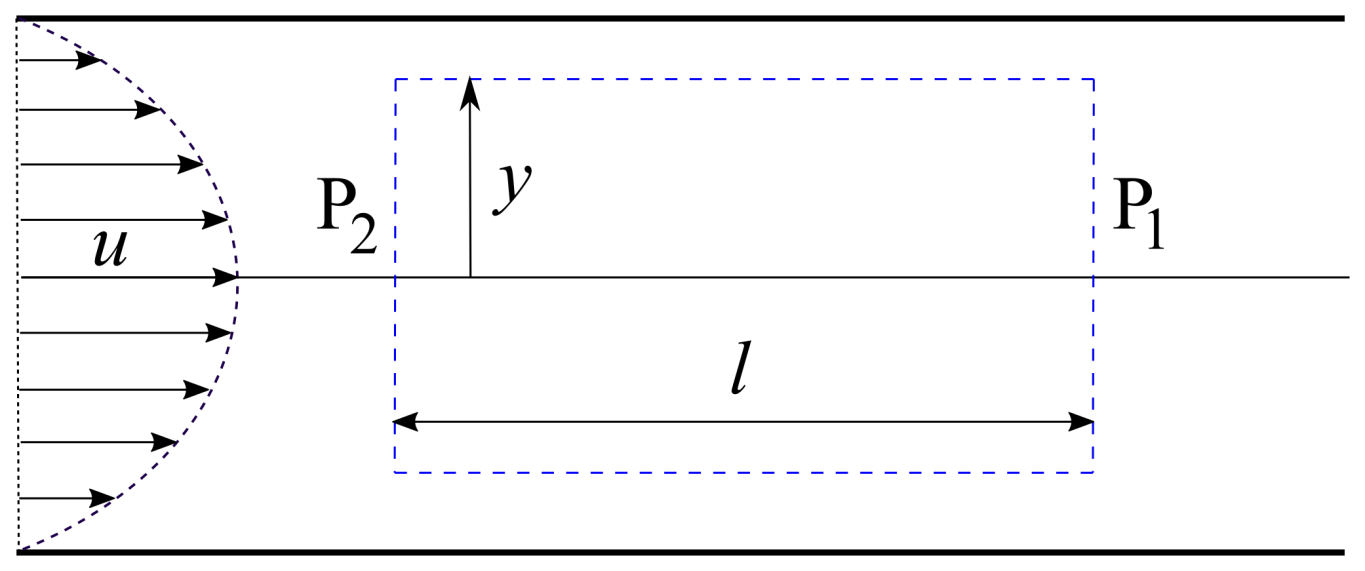
Рисунок 11. Распределение скоростей в круглой трубе и мысленно выделенный цилиндр.
Выделим в газе малый цилиндр радиуса
 и длины
и длины 
. Обозначим давления на его торцах
 и Р2. В режиме установившегося течения сила давления на выделенный цилиндр
и Р2. В режиме установившегося течения сила давления на выделенный цилиндр  (5.10)
(5.10) уравновешивается силой внутреннего трения, действующей на поверхность цилиндра со стороны окружающих его слоев газа. Условие стационарности потока тогда запишется как
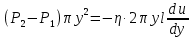 , (5.11)
, (5.11) откуда
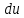 равно
равно . (5.12)
. (5.12) Интегрируя это равенство по у, найдем
 , (5.13)
, (5.13) где
 – постоянная интегрирования, которую найдем из граничного условия.
– постоянная интегрирования, которую найдем из граничного условия.При
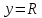 скорость газа обращается в нуль – т.е. молекулы газа как бы прилипают к стенке (движение молекул газа здесь тормозится до нуля, из-за взаимодействия их с молекулами стенки). Тогда
скорость газа обращается в нуль – т.е. молекулы газа как бы прилипают к стенке (движение молекул газа здесь тормозится до нуля, из-за взаимодействия их с молекулами стенки). Тогда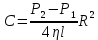 . (5.14)
. (5.14) Для зависимости скорости слоя газа от его координаты получили
 . (5.15)
. (5.15) Скорость максимальна на оси трубы и квадратично убывает до нуля с приближением к стенке (см. рис.2).
Объем
 газа, протекающий через трубу за время
газа, протекающий через трубу за время , находится интегрированием и равен
, находится интегрированием и равен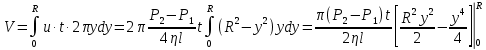 ,
,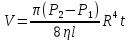 . (5.16)
. (5.16)Это равенство называется формулой Пуазейля-Хагена. Используя ее, можно экспериментально определить вязкость газа, если известен объем газа
 , прошедший через трубку длиной
, прошедший через трубку длиной  за время
за время  , ее радиус
, ее радиус 
и перепад давления на торцах трубы:
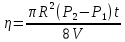 . (5.17)
. (5.17) При рассмотрении выше течение газа считалось ламинарным (расслоенным). Кроме ламинарного течения существует еще турбулентное течение, при котором слои выделить нельзя. Характер течения газа (жидкости) определяется числом Рейнольда Re:
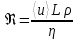 , (5.18)
, (5.18) где
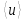 - средняя скорость потока,
- средняя скорость потока,  – характерный размер,
– характерный размер, 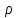 – плотность газа,
– плотность газа,  – вязкость.
– вязкость. В длинных гладких трубах круглого сечения ламинарный характер потока сохраняется при Re < 2300 (при вычислении числа Рейнольдса берется
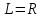 ). У резких внешних границ круглых труб даже при Re < 2300 возможны области турбулентного движения. Расстояние
). У резких внешних границ круглых труб даже при Re < 2300 возможны области турбулентного движения. Расстояние 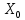 , после которого устанавливается ламинарный поток, приблизительно можно оценить по формуле
, после которого устанавливается ламинарный поток, приблизительно можно оценить по формуле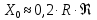 . (5.19)
. (5.19) Хорошие результаты описанный метод дает при
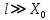 . Как следствие, для проверки обоснованности результатов, полученных на капиллярном вискозиметре, нам надо подсчитать число Рейнольдса и сравнить его с критическим значением. Также требуется оценить значение
. Как следствие, для проверки обоснованности результатов, полученных на капиллярном вискозиметре, нам надо подсчитать число Рейнольдса и сравнить его с критическим значением. Также требуется оценить значение 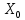 и сравнить его с длиной используемого капилляра.
и сравнить его с длиной используемого капилляра.Для оценки чисел Re и
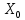 , средняя скорость потока находится из очевидного равенства
, средняя скорость потока находится из очевидного равенства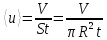 . (5.20)
. (5.20) ОПИСАНИЕ ЭКСПЕРИМЕНТАЛЬНОЙ УСТАНОВКИ

Рисунок 12. Схема экспериментальной установки.