ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 08.11.2023
Просмотров: 143
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
СОДЕРЖАНИЕ
2. ОПРЕДЕЛЕНИЕ КОЭФФИЦИЕНТА ПОВЕРХНОСТНОГО НАТЯЖЕНИЯ.
3. ОПРЕДЕЛЕНИЕ КОЭФФИЦИЕНТА ЛИНЕЙНОГО РАСШИРЕНИЯ МЕТАЛЛОВ
4. ОПРЕДЕЛЕНИЕ УДЕЛЬНОЙ ТЕПЛОЕМКОСТИ ТВЕРДЫХ ТЕЛ.
5. ОПРЕДЕЛЕНИЕ КОЭФФИЦИЕНТА ВЯЗКОСТИ ГАЗОВ И СРЕДНЕЙ ДЛИНЫ ПРОБЕГА МОЛЕКУЛ.
6. ОПРЕДЕЛЕНИЕ ПОКАЗАТЕЛЯ АДИАБАТЫ ДЛЯ ВОЗДУХА МЕТОДОМ КЛЕМАНА-ДЕЗОРМА.
1, Т2 и Т3 на рисунке 5). Асимметрия потенциала приводит к тому, что при колебаниях атом находится на расстояниях, больших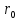 
, дольше, чем на расстояниях, меньших 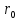. Среднее по времени расстояние между атомами становится больше, чем 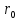- с повышением температуры среднее по времени расстояние между атомами увеличивается.
Надо отметить, что новее среднее положение колеблющегося атома соответствует равенству нулю средней силы, действующей на него. Если среднее расстояние не увеличится, то средняя сила, действующая на колеблющийся атом, окажется ненулевой и направленной в сторону меньших значений расстояния. Это неучтенная здесь внешняя сжимающая сила. Она может присутствовать в кристаллах, если образец кристалла сдавливают.
Количественно тепловое расширение характеризуется коэффициентами линейного и объемного расширения, которые определяются следующим образом. Пусть тело длиной l0 при изменении температуры на Т изменяет свою длину на l. Обычно при малых изменениях температуры соответствующая зависимость линейная, поэтому коэффициент линейного расширения определяется как относительное изменение длины образца, деленное на изменение температуры, вызвавшего это удлинение:
(3.1)
Точно так же коэффициент объемного расширения
определяется из соотношения
(3.2)
где V0 – начальный объем тела, V изменение объема тела при изменении его температуры на Т.
Вследствие анизотропии кристаллов коэффициент линейного расширения монокристаллических тел может быть различным в разных направлениях. Это означает, что если из данного кристалла вырезать шар, то после его нагревания он потеряет свою сферическую форму. Можно показать, что в самом общем случае такой шар при нагревании превращается в трехосный эллипсоид, оси которого связаны с кристаллографическими осями атома кристалла. Коэффициенты теплового расширения по трем осям эллипсоида называются главными коэффициентами расширения кристалла. Если их обозначить соответственно через
1, 2, 3, то коэффициент объемного расширения кристалла
(3.3)
Шар, вырезанный из кристаллов с кубической симметрией (как и из изотропных тел), остаётся шаром и после нагревания. Коэффициенты линейного и объемного расширения практически остаются постоянными, если интервалы температур, в которых они измеряются, малы, а сами температуры высокие. Вообще же коэффициенты теплового расширения зависят от температуры.
ОПИСАНИЕ ЭКСПЕРИМЕНТАЛЬНОЙ УСТАНОВКИ
И
спытуемый образец твердого тела нагревается в воде, находящейся в стеклянной пробирке. Изменение длины нагретого образца по сравнению с его первоначальной длиной (при комнатной температуре) измеряется индикатором малых перемещений.
П
Рисунок 6
рибор (Рис. 6) состоит из корпуса 1, к которому крепится защитный кожух 2. Внутри кожуха установлен нагреватель, центрирующийся с торцов в опоре и крышке 3. Электрическая схема прибора состоит из нагревателя на базе эмалированного сопротивления, соединенного последовательно с предохранителем и индикаторной лампой. При проведении опытов в нагреватель через прокладку помещается стеклянная пробирка 4 со стержнем 5. На корпусе прибора установлена стойка с кронштейном для индикатора малых перемещений 6. Кронштейн может поворачиваться вокруг оси стойки на 900. На панели корпуса расположены индикаторная лампа 7 и кнопочный выключатель 8, а на внутренней перегородке – винт заземления. Внутри корпуса на опоре расположен держатель с предохранителем.
Рисунок 7. Внешний вид установки.
ПОРЯДОК ВЫПОЛНЕНИЯ РАБОТЫ И ОБРАБОТКА ИЗМЕРЕНИЙ
1. Пробирки из комплекта принадлежностей прибора на ½ объема наполнить водой комнатной температуры, опустить в каждую по испытуемому стержню и поместить на штатив.
2. Обратить внимание на то, чтобы сферический конец стержня упирался в дно пробирки.
3. Проверить заземление прибора!
4. Штепсельную вилку прибора включить в сеть 220 В.
5. В поворотный кронштейн вставить индикатор и отвести его на четверть оборота в сторону до упора.
6. Лабораторным термометром замерить температуру воды в одной из пробирок (стержень при этом извлекается из пробирки).
7. Пробирку с испытуемым стержнем через резиновую прокладку и отверстие в крышке прибора ввести в нагреватель.
8. Оттянуть шток индикатора вверх, установить индикатор над пробиркой (повернуть кронштейн в прорези до упора) и опустить шток в углубление на торце стержня.
9. Заметить положение на шкале индикатора (для первого опыта стрелку ставить на нулевую отметку).
10. Включить питание прибора кнопочным выключателем. При этом должна загореться индикаторная лампа.
При закипании воды в пробирке испытуемый образец принимает температуру, равную температуре кипения воды. Увеличение длины образца определяется по отклонению стрелки индикатора от первоначального положения. Отсчет ведут с точностью до половины деления шкалы индикатора, т.е. с точностью до 5 микрон.
Для продолжения работы и проведения опытов с другими образцами необходимо:
1. Кнопочным выключателем отключить питание прибора.
2. Индикатор на поворотном кронштейне отвести в сторону до упора.
3. Извлечь из прибора нагретую пробирку и поместить её в штатив.
4. Повторить операции 5-10 для другого образца.
Поскольку дальнейшая работа проводится при «разогретом» приборе, во избежание заметных искажений в замерах, время с момента помещения пробирки в зону нагрева до фиксации первоначального положения стрелки индикатора не должно превышать 30-40 сек. По окончании работы с прибором (после снятия показаний по всем образцам) необходимо рассчитать значения коэффициента линейного расширения, используя формулу
,
где
- увеличение длины образца, 
- начальная длина образца, 
- первоначальная температура в пробирке, 
- конечная температура воды в пробирке после нагревания.
Экспериментальные данные и результаты расчета для каждого образца занести в таблицы. Окончательный результат для каждого образца необходимо представить в виде α = α
ср
Δα.
ТАБЛИЦЫ
Таблица № 3.1
КОНТРОЛЬНЫЕ ВОПРОСЫ
ЛИТЕРАТУРА.
1. Савельев И.В. Курс физики. Т. 1. М., «Наука», 1987.
2. Сивухин Д.В. «Общий курс физики», Т. II, - М.: Физматлит, 2005
3. Матвеев А.Н. Молекулярная физика. М., «Высшая школа», 1987
4. Яковлев В.Ф. Курс физики. Теплота и молекулярная физика. М., «Просвещение», 1976.
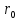, дольше, чем на расстояниях, меньших 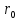. Среднее по времени расстояние между атомами становится больше, чем 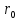- с повышением температуры среднее по времени расстояние между атомами увеличивается. Надо отметить, что новее среднее положение колеблющегося атома соответствует равенству нулю средней силы, действующей на него. Если среднее расстояние не увеличится, то средняя сила, действующая на колеблющийся атом, окажется ненулевой и направленной в сторону меньших значений расстояния. Это неучтенная здесь внешняя сжимающая сила. Она может присутствовать в кристаллах, если образец кристалла сдавливают.
Количественно тепловое расширение характеризуется коэффициентами линейного и объемного расширения, которые определяются следующим образом. Пусть тело длиной l0 при изменении температуры на Т изменяет свою длину на l. Обычно при малых изменениях температуры соответствующая зависимость линейная, поэтому коэффициент линейного расширения определяется как относительное изменение длины образца, деленное на изменение температуры, вызвавшего это удлинение:
(3.1) Точно так же коэффициент объемного расширения
определяется из соотношения (3.2) где V0 – начальный объем тела, V изменение объема тела при изменении его температуры на Т.
Вследствие анизотропии кристаллов коэффициент линейного расширения монокристаллических тел может быть различным в разных направлениях. Это означает, что если из данного кристалла вырезать шар, то после его нагревания он потеряет свою сферическую форму. Можно показать, что в самом общем случае такой шар при нагревании превращается в трехосный эллипсоид, оси которого связаны с кристаллографическими осями атома кристалла. Коэффициенты теплового расширения по трем осям эллипсоида называются главными коэффициентами расширения кристалла. Если их обозначить соответственно через
1, 2, 3, то коэффициент объемного расширения кристалла
(3.3) Шар, вырезанный из кристаллов с кубической симметрией (как и из изотропных тел), остаётся шаром и после нагревания. Коэффициенты линейного и объемного расширения практически остаются постоянными, если интервалы температур, в которых они измеряются, малы, а сами температуры высокие. Вообще же коэффициенты теплового расширения зависят от температуры.
ОПИСАНИЕ ЭКСПЕРИМЕНТАЛЬНОЙ УСТАНОВКИ
И
спытуемый образец твердого тела нагревается в воде, находящейся в стеклянной пробирке. Изменение длины нагретого образца по сравнению с его первоначальной длиной (при комнатной температуре) измеряется индикатором малых перемещений. П
Рисунок 6
рибор (Рис. 6) состоит из корпуса 1, к которому крепится защитный кожух 2. Внутри кожуха установлен нагреватель, центрирующийся с торцов в опоре и крышке 3. Электрическая схема прибора состоит из нагревателя на базе эмалированного сопротивления, соединенного последовательно с предохранителем и индикаторной лампой. При проведении опытов в нагреватель через прокладку помещается стеклянная пробирка 4 со стержнем 5. На корпусе прибора установлена стойка с кронштейном для индикатора малых перемещений 6. Кронштейн может поворачиваться вокруг оси стойки на 900. На панели корпуса расположены индикаторная лампа 7 и кнопочный выключатель 8, а на внутренней перегородке – винт заземления. Внутри корпуса на опоре расположен держатель с предохранителем.
Рисунок 7. Внешний вид установки.
ПОРЯДОК ВЫПОЛНЕНИЯ РАБОТЫ И ОБРАБОТКА ИЗМЕРЕНИЙ
1. Пробирки из комплекта принадлежностей прибора на ½ объема наполнить водой комнатной температуры, опустить в каждую по испытуемому стержню и поместить на штатив.
2. Обратить внимание на то, чтобы сферический конец стержня упирался в дно пробирки.
3. Проверить заземление прибора!
4. Штепсельную вилку прибора включить в сеть 220 В.
5. В поворотный кронштейн вставить индикатор и отвести его на четверть оборота в сторону до упора.
6. Лабораторным термометром замерить температуру воды в одной из пробирок (стержень при этом извлекается из пробирки).
7. Пробирку с испытуемым стержнем через резиновую прокладку и отверстие в крышке прибора ввести в нагреватель.
8. Оттянуть шток индикатора вверх, установить индикатор над пробиркой (повернуть кронштейн в прорези до упора) и опустить шток в углубление на торце стержня.
9. Заметить положение на шкале индикатора (для первого опыта стрелку ставить на нулевую отметку).
10. Включить питание прибора кнопочным выключателем. При этом должна загореться индикаторная лампа.
При закипании воды в пробирке испытуемый образец принимает температуру, равную температуре кипения воды. Увеличение длины образца определяется по отклонению стрелки индикатора от первоначального положения. Отсчет ведут с точностью до половины деления шкалы индикатора, т.е. с точностью до 5 микрон.
Для продолжения работы и проведения опытов с другими образцами необходимо:
1. Кнопочным выключателем отключить питание прибора.
2. Индикатор на поворотном кронштейне отвести в сторону до упора.
3. Извлечь из прибора нагретую пробирку и поместить её в штатив.
4. Повторить операции 5-10 для другого образца.
Поскольку дальнейшая работа проводится при «разогретом» приборе, во избежание заметных искажений в замерах, время с момента помещения пробирки в зону нагрева до фиксации первоначального положения стрелки индикатора не должно превышать 30-40 сек. По окончании работы с прибором (после снятия показаний по всем образцам) необходимо рассчитать значения коэффициента линейного расширения, используя формулу
,где
- увеличение длины образца, - начальная длина образца, - первоначальная температура в пробирке, - конечная температура воды в пробирке после нагревания.Экспериментальные данные и результаты расчета для каждого образца занести в таблицы. Окончательный результат для каждого образца необходимо представить в виде α = α
ср
Δα.ТАБЛИЦЫ
Таблица № 3.1
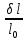| П/п | ,  | , |  , мм |  , мкм | 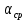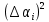 |  , |  , 1/ |  , 1/ |  , 1/ |  , 1/ |  , 1/ |
| 1. 2. 3. 4. 5. | | | | | | | | | | | |
| Ср.зн. | | | | | | | | | | | |
КОНТРОЛЬНЫЕ ВОПРОСЫ
-
Что такое тепловое расширение тел? -
Что такое коэффициент линейного расширения, коэффициент объемного расширения вещества? -
Возможно, ли описать тепловое расширение твердого тела, рассматривая его как систему гармонических осцилляторов? Если да, то как? Если нет, то почему? -
Как по величине коэффициента линейного расширения определить коэффициент объёмного расширения для данного вещества?
ЛИТЕРАТУРА.
1. Савельев И.В. Курс физики. Т. 1. М., «Наука», 1987.
2. Сивухин Д.В. «Общий курс физики», Т. II, - М.: Физматлит, 2005
3. Матвеев А.Н. Молекулярная физика. М., «Высшая школа», 1987
4. Яковлев В.Ф. Курс физики. Теплота и молекулярная физика. М., «Просвещение», 1976.
- 1 2 3 4 5 6 7