ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 08.11.2023
Просмотров: 138
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
СОДЕРЖАНИЕ
2. ОПРЕДЕЛЕНИЕ КОЭФФИЦИЕНТА ПОВЕРХНОСТНОГО НАТЯЖЕНИЯ.
3. ОПРЕДЕЛЕНИЕ КОЭФФИЦИЕНТА ЛИНЕЙНОГО РАСШИРЕНИЯ МЕТАЛЛОВ
4. ОПРЕДЕЛЕНИЕ УДЕЛЬНОЙ ТЕПЛОЕМКОСТИ ТВЕРДЫХ ТЕЛ.
5. ОПРЕДЕЛЕНИЕ КОЭФФИЦИЕНТА ВЯЗКОСТИ ГАЗОВ И СРЕДНЕЙ ДЛИНЫ ПРОБЕГА МОЛЕКУЛ.
6. ОПРЕДЕЛЕНИЕ ПОКАЗАТЕЛЯ АДИАБАТЫ ДЛЯ ВОЗДУХА МЕТОДОМ КЛЕМАНА-ДЕЗОРМА.
, получим
 . (6.11)
. (6.11)
Если нагревание проводилось при постоянном давлении, молярная теплоемкость обозначается и называется изобарной. Она равна
и называется изобарной. Она равна
 . (6.12)
. (6.12)
Воспользовавшись справедливым для идеального газа уравнением Менделеева-Клапейрона
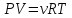 , (6.13)
, (6.13)
дифференцирование которого при постоянном давлении дает
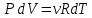 , (6.14)
, (6.14)
получаем
 , (6.15)
, (6.15)
Связь между и
и  :
:
 (6.16)
(6.16)
называется уравнением Майера.
Одним из важнейших термодинамических процессов является адиабатический. Это такой термодинамический процесс, при котором система не получает и не отдаёт теплоты.
Есть два основных способа сделать процесс изменения состояния газа приблизительно адиабатическим. Первый состоит в том, что обеспечивается хорошая теплоизоляция рассматриваемой системы, а процесс ее расширения или сжатия проводится очень медленно. Требования к теплоизоляции являются при этом очень жесткими. Второй способ заключается в том, что процесс проводят достаточно быстро для того, чтобы за время его протекания не успел произойти существенный теплообмен с окружающей средой. В то же время длительность процесса должна быть достаточной для поддержания термодинамического равновесия между отдельными частями системы. Теплоизоляция газа оказывается несущественной.
Поскольку при адиабатическом процессе , Первое начало принимает вид
, Первое начало принимает вид
 , (6.17)
, (6.17)
т.е. в условиях адиабатической изолированности расширение газа приводит к уменьшению его внутренней энергии и, наоборот, процесс совершения работы над газом (по его сжатию, ) будет приводить к повышению внутренней энергии газа. Уравнение адиабатического процесса получим, записав Первое начало (для одного моля газа) с учетом
) будет приводить к повышению внутренней энергии газа. Уравнение адиабатического процесса получим, записав Первое начало (для одного моля газа) с учетом
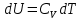 :
:
 . (6.18)
. (6.18)
Затем продифференцируем уравнение Менделеева-Клапейрона для одного моля
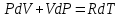 . (6.19)
. (6.19)
Разделив это уравнение на предыдущее, получим
 , (6.20)
, (6.20)
С учетом уравнения Майера уравнение переписывается как
 , (6.21)
, (6.21)
где называют показателем адиабаты. Это уравнение перепишем в виде
называют показателем адиабаты. Это уравнение перепишем в виде
 (6.22)
(6.22)
и после интегрирования получим
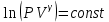 . (6.23)
. (6.23)
Тогда уравнение адиабатического процесса имеет вид
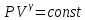 . (6.24)
. (6.24)
Полученное выражение называется уравнением Пуассона.
МЕТОД КЛЕМАНА-ДЕЗОРМА ОПРЕДЕЛЕНИЯ ПОКАЗАТЕЛЯ АДИАБАТЫ
О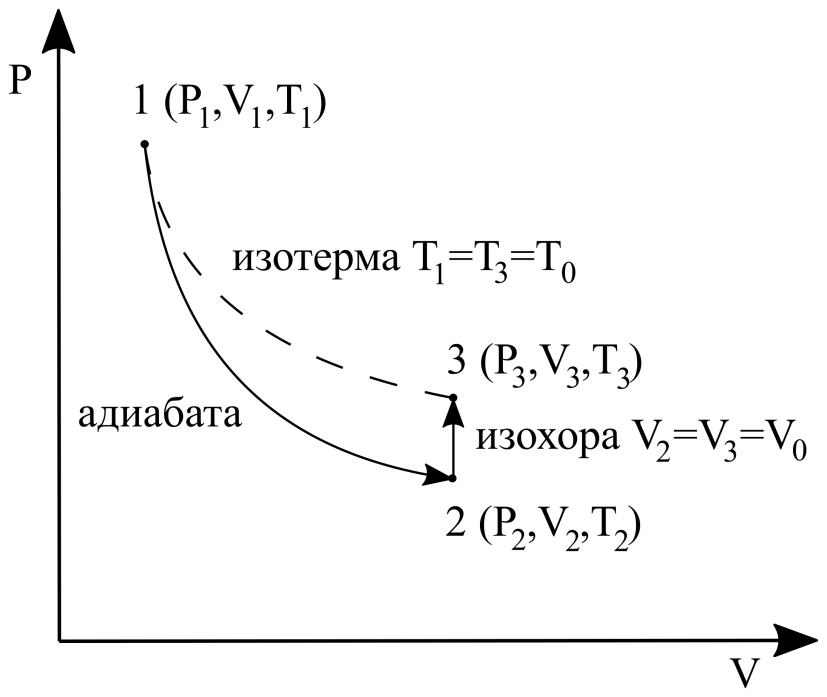
Рисунок 14. К принципу метода Клемана-Дезорма
пределение показателя адиабаты методом Клемана и Дезорма основывается на использовании двух последовательных процессов изменения параметра газа – адиабатического и изохорного.
Пусть некоторый газ изначально имеет объем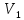 , температуру
, температуру 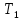 и находится под давлением
и находится под давлением  . На графике (Рис. 14) в координатах
. На графике (Рис. 14) в координатах  ,
,  это соответствует состоянию 1. Этому газу позволяют адиабатически расшириться и перейти в состояние 2 (давление
это соответствует состоянию 1. Этому газу позволяют адиабатически расшириться и перейти в состояние 2 (давление  , температура
, температура 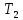 , объем
, объем 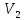
). Поскольку имеет место адиабатическое расширение, газ охлаждается ( ). Затем газ нагревают при постоянном объеме до исходной температуры. Конечное состояние 3 соответствует давлению
). Затем газ нагревают при постоянном объеме до исходной температуры. Конечное состояние 3 соответствует давлению  , температуре
, температуре 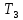 , объему
, объему  . В силу наложенных условий, имеем (см. Рис. 14)
. В силу наложенных условий, имеем (см. Рис. 14)
 , (6.25)
, (6.25)
 . (6.26)
. (6.26)
Параметры состояний 1 и 2 связаны уравнением Пуассона
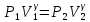 , (6.27)
, (6.27)
т.е.
 . (6.28)
. (6.28)
Параметры состояний 1 и 3 связаны уравнением изотермы
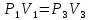 , (6.29)
, (6.29)
т.е.
 . (6.30)
. (6.30)
Из этих уравнений
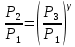 . (6.31)
. (6.31)
Из этого уравнения следует, что для определения показателя адиабаты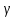 нам достаточно знать давления
нам достаточно знать давления  ,
,  ,
,  .
.
Теперь предположим, что имеется возможность измерять разности давлений и
и 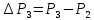 , причем эти разности оказываются малыми по сравнению с
, причем эти разности оказываются малыми по сравнению с  . Соотношение (6.31) принимает вид
. Соотношение (6.31) принимает вид
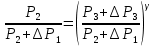 (6.32)
(6.32)
или
 . (6.33)
. (6.33)
В режиме ,
, 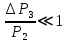
, с достаточной точностью можно ограничиться только двумя членами в разложении сумм в (6.35) по степеням γ-1 и γ
 . (6.34)
. (6.34)
Отсюда уже можно найти значение
 . (6.35)
. (6.35)
ОПИСАНИЕ ЭКСПЕРИМЕНТАЛЬНОЙ УСТАНОВКИ И МЕТОДИКИ ЭКСПЕРИМЕНТА
С
Рисунок 15. Схема экспериментальной установки.
хема установки, используемой в работе для реализации описанного выше процесса и измерения разностей давлений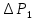 и
и 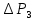 , показана на рис.3. Установка для определения показателя адиабаты состоит из стеклянного баллона, заполненного воздухом, соединенного с U-образным водяным манометром и насосом (Рис. 15). При закрытом кране
, показана на рис.3. Установка для определения показателя адиабаты состоит из стеклянного баллона, заполненного воздухом, соединенного с U-образным водяным манометром и насосом (Рис. 15). При закрытом кране  и открытом кране
и открытом кране  в баллон дополнительно накачивается небольшое количество воздуха, после чего кран
в баллон дополнительно накачивается небольшое количество воздуха, после чего кран  закрывается. Давление в баллоне увеличивается, температура газа в баллоне также увеличивается, становясь чуть выше комнатной. Затем, после некоторого промежутка времени, устанавливается тепловое равновесие, то есть температура газа опускается до комнатной. Таким образом, некоторая порция газа в баллоне приходит в исходное состояние 1 (см. Рис. 14). После открытия крана
закрывается. Давление в баллоне увеличивается, температура газа в баллоне также увеличивается, становясь чуть выше комнатной. Затем, после некоторого промежутка времени, устанавливается тепловое равновесие, то есть температура газа опускается до комнатной. Таким образом, некоторая порция газа в баллоне приходит в исходное состояние 1 (см. Рис. 14). После открытия крана  эта порция газа расширяется, пока ее давление не сравняется с атмосферным давлением. В этот момент кран
эта порция газа расширяется, пока ее давление не сравняется с атмосферным давлением. В этот момент кран  закрывается и порция газа оказывается в состоянии 2. Её объем в этот момент равен объему стеклянного баллона
закрывается и порция газа оказывается в состоянии 2. Её объем в этот момент равен объему стеклянного баллона 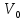 . Переход порции газа в состояние 3 происходит уже при постоянном объеме. Таким образом, реализована последовательность процессов метода Клемана и Дезорма.
. Переход порции газа в состояние 3 происходит уже при постоянном объеме. Таким образом, реализована последовательность процессов метода Клемана и Дезорма.
При проведении эксперимента на данной лабораторной установке температура
равна температуре воздуха в комнате, а давление равно атмосферному давлению. Так как
равно атмосферному давлению. Так как 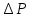 измеряется водяным манометром, то
измеряется водяным манометром, то 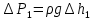 ,
, 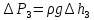 , где
, где  и
и  , разность высот уровней воды в коленах манометра, соответственно для состояний 1 и 3. Тогда выражение для расчета γ будет иметь вид:
, разность высот уровней воды в коленах манометра, соответственно для состояний 1 и 3. Тогда выражение для расчета γ будет иметь вид:
 . (6.36)
. (6.36)
Описание эксперимента выше крайне идеализированное. На практике закрыть кран точно в момент выравнивания давления газа в баллоне с атмосферным давлением невозможно. По показаниям U-образного манометра определить момент выравнивания давлений нельзя из-за инерционности манометра (вода между его коленами перетекает медленно, в манометре могут
точно в момент выравнивания давления газа в баллоне с атмосферным давлением невозможно. По показаниям U-образного манометра определить момент выравнивания давлений нельзя из-за инерционности манометра (вода между его коленами перетекает медленно, в манометре могут
в
Рисунок 16. Иллюстрация реального процесса в эксперименте.
озникать колебания уровня воды в коленах). Также надо учесть инерционность крана . Оценка показывает, что для данной установки длительность процесса 1
. Оценка показывает, что для данной установки длительность процесса 1  2 составляет только 0,1-0,3 секунды. Поэтому после состояния 2 порция газа некоторое время расширяется при постоянном давлении, переходя из состояния 2 в состояние 4 (см. Рис. 16), а по достижению состояния 4 начинается процесс изохорного перехода в состояние 5. Точность измерения показателя адиабаты
2 составляет только 0,1-0,3 секунды. Поэтому после состояния 2 порция газа некоторое время расширяется при постоянном давлении, переходя из состояния 2 в состояние 4 (см. Рис. 16), а по достижению состояния 4 начинается процесс изохорного перехода в состояние 5. Точность измерения показателя адиабаты  можно улучшить, если значение
можно улучшить, если значение  , соответствующее состоянию 3, определять из серии измерений при разных временах открытия клапана
, соответствующее состоянию 3, определять из серии измерений при разных временах открытия клапана  с помощью графической экстраполяции.
с помощью графической экстраполяции.
 . (6.11)
. (6.11) Если нагревание проводилось при постоянном давлении, молярная теплоемкость обозначается
 и называется изобарной. Она равна
и называется изобарной. Она равна . (6.12)
. (6.12) Воспользовавшись справедливым для идеального газа уравнением Менделеева-Клапейрона
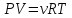 , (6.13)
, (6.13) дифференцирование которого при постоянном давлении дает
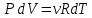 , (6.14)
, (6.14) получаем
 , (6.15)
, (6.15) Связь между
 и
и  :
: (6.16)
(6.16) называется уравнением Майера.
Одним из важнейших термодинамических процессов является адиабатический. Это такой термодинамический процесс, при котором система не получает и не отдаёт теплоты.
Есть два основных способа сделать процесс изменения состояния газа приблизительно адиабатическим. Первый состоит в том, что обеспечивается хорошая теплоизоляция рассматриваемой системы, а процесс ее расширения или сжатия проводится очень медленно. Требования к теплоизоляции являются при этом очень жесткими. Второй способ заключается в том, что процесс проводят достаточно быстро для того, чтобы за время его протекания не успел произойти существенный теплообмен с окружающей средой. В то же время длительность процесса должна быть достаточной для поддержания термодинамического равновесия между отдельными частями системы. Теплоизоляция газа оказывается несущественной.
Поскольку при адиабатическом процессе
 , Первое начало принимает вид
, Первое начало принимает вид  , (6.17)
, (6.17) т.е. в условиях адиабатической изолированности расширение газа приводит к уменьшению его внутренней энергии и, наоборот, процесс совершения работы над газом (по его сжатию,
 ) будет приводить к повышению внутренней энергии газа. Уравнение адиабатического процесса получим, записав Первое начало (для одного моля газа) с учетом
) будет приводить к повышению внутренней энергии газа. Уравнение адиабатического процесса получим, записав Первое начало (для одного моля газа) с учетом
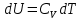 :
: . (6.18)
. (6.18) Затем продифференцируем уравнение Менделеева-Клапейрона для одного моля
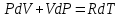 . (6.19)
. (6.19) Разделив это уравнение на предыдущее, получим
 , (6.20)
, (6.20) С учетом уравнения Майера уравнение переписывается как
 , (6.21)
, (6.21) где
 называют показателем адиабаты. Это уравнение перепишем в виде
называют показателем адиабаты. Это уравнение перепишем в виде  (6.22)
(6.22) и после интегрирования получим
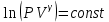 . (6.23)
. (6.23) Тогда уравнение адиабатического процесса имеет вид
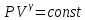 . (6.24)
. (6.24) Полученное выражение называется уравнением Пуассона.
МЕТОД КЛЕМАНА-ДЕЗОРМА ОПРЕДЕЛЕНИЯ ПОКАЗАТЕЛЯ АДИАБАТЫ
О

Рисунок 14. К принципу метода Клемана-Дезорма
пределение показателя адиабаты методом Клемана и Дезорма основывается на использовании двух последовательных процессов изменения параметра газа – адиабатического и изохорного.
Пусть некоторый газ изначально имеет объем
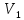 , температуру
, температуру 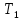 и находится под давлением
и находится под давлением  . На графике (Рис. 14) в координатах
. На графике (Рис. 14) в координатах  ,
,  это соответствует состоянию 1. Этому газу позволяют адиабатически расшириться и перейти в состояние 2 (давление
это соответствует состоянию 1. Этому газу позволяют адиабатически расшириться и перейти в состояние 2 (давление  , температура
, температура 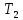 , объем
, объем 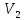
). Поскольку имеет место адиабатическое расширение, газ охлаждается (
 ). Затем газ нагревают при постоянном объеме до исходной температуры. Конечное состояние 3 соответствует давлению
). Затем газ нагревают при постоянном объеме до исходной температуры. Конечное состояние 3 соответствует давлению  , температуре
, температуре 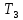 , объему
, объему  . В силу наложенных условий, имеем (см. Рис. 14)
. В силу наложенных условий, имеем (см. Рис. 14) , (6.25)
, (6.25)  . (6.26)
. (6.26) Параметры состояний 1 и 2 связаны уравнением Пуассона
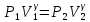 , (6.27)
, (6.27) т.е.
 . (6.28)
. (6.28) Параметры состояний 1 и 3 связаны уравнением изотермы
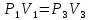 , (6.29)
, (6.29) т.е.
 . (6.30)
. (6.30) Из этих уравнений
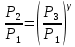 . (6.31)
. (6.31) Из этого уравнения следует, что для определения показателя адиабаты
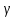 нам достаточно знать давления
нам достаточно знать давления  ,
,  ,
,  .
.Теперь предположим, что имеется возможность измерять разности давлений
 и
и 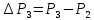 , причем эти разности оказываются малыми по сравнению с
, причем эти разности оказываются малыми по сравнению с  . Соотношение (6.31) принимает вид
. Соотношение (6.31) принимает вид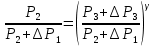 (6.32)
(6.32) или
 . (6.33)
. (6.33) В режиме
 ,
, 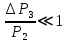
, с достаточной точностью можно ограничиться только двумя членами в разложении сумм в (6.35) по степеням γ-1 и γ
 . (6.34)
. (6.34) Отсюда уже можно найти значение
 . (6.35)
. (6.35) ОПИСАНИЕ ЭКСПЕРИМЕНТАЛЬНОЙ УСТАНОВКИ И МЕТОДИКИ ЭКСПЕРИМЕНТА
С

Рисунок 15. Схема экспериментальной установки.
хема установки, используемой в работе для реализации описанного выше процесса и измерения разностей давлений
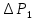 и
и 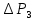 , показана на рис.3. Установка для определения показателя адиабаты состоит из стеклянного баллона, заполненного воздухом, соединенного с U-образным водяным манометром и насосом (Рис. 15). При закрытом кране
, показана на рис.3. Установка для определения показателя адиабаты состоит из стеклянного баллона, заполненного воздухом, соединенного с U-образным водяным манометром и насосом (Рис. 15). При закрытом кране  и открытом кране
и открытом кране  в баллон дополнительно накачивается небольшое количество воздуха, после чего кран
в баллон дополнительно накачивается небольшое количество воздуха, после чего кран  закрывается. Давление в баллоне увеличивается, температура газа в баллоне также увеличивается, становясь чуть выше комнатной. Затем, после некоторого промежутка времени, устанавливается тепловое равновесие, то есть температура газа опускается до комнатной. Таким образом, некоторая порция газа в баллоне приходит в исходное состояние 1 (см. Рис. 14). После открытия крана
закрывается. Давление в баллоне увеличивается, температура газа в баллоне также увеличивается, становясь чуть выше комнатной. Затем, после некоторого промежутка времени, устанавливается тепловое равновесие, то есть температура газа опускается до комнатной. Таким образом, некоторая порция газа в баллоне приходит в исходное состояние 1 (см. Рис. 14). После открытия крана  эта порция газа расширяется, пока ее давление не сравняется с атмосферным давлением. В этот момент кран
эта порция газа расширяется, пока ее давление не сравняется с атмосферным давлением. В этот момент кран  закрывается и порция газа оказывается в состоянии 2. Её объем в этот момент равен объему стеклянного баллона
закрывается и порция газа оказывается в состоянии 2. Её объем в этот момент равен объему стеклянного баллона 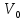 . Переход порции газа в состояние 3 происходит уже при постоянном объеме. Таким образом, реализована последовательность процессов метода Клемана и Дезорма.
. Переход порции газа в состояние 3 происходит уже при постоянном объеме. Таким образом, реализована последовательность процессов метода Клемана и Дезорма. При проведении эксперимента на данной лабораторной установке температура

равна температуре воздуха в комнате, а давление
 равно атмосферному давлению. Так как
равно атмосферному давлению. Так как 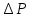 измеряется водяным манометром, то
измеряется водяным манометром, то 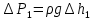 ,
, 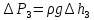 , где
, где  и
и  , разность высот уровней воды в коленах манометра, соответственно для состояний 1 и 3. Тогда выражение для расчета γ будет иметь вид:
, разность высот уровней воды в коленах манометра, соответственно для состояний 1 и 3. Тогда выражение для расчета γ будет иметь вид: . (6.36)
. (6.36)Описание эксперимента выше крайне идеализированное. На практике закрыть кран
 точно в момент выравнивания давления газа в баллоне с атмосферным давлением невозможно. По показаниям U-образного манометра определить момент выравнивания давлений нельзя из-за инерционности манометра (вода между его коленами перетекает медленно, в манометре могут
точно в момент выравнивания давления газа в баллоне с атмосферным давлением невозможно. По показаниям U-образного манометра определить момент выравнивания давлений нельзя из-за инерционности манометра (вода между его коленами перетекает медленно, в манометре могут в

Рисунок 16. Иллюстрация реального процесса в эксперименте.
озникать колебания уровня воды в коленах). Также надо учесть инерционность крана
 . Оценка показывает, что для данной установки длительность процесса 1
. Оценка показывает, что для данной установки длительность процесса 1  2 составляет только 0,1-0,3 секунды. Поэтому после состояния 2 порция газа некоторое время расширяется при постоянном давлении, переходя из состояния 2 в состояние 4 (см. Рис. 16), а по достижению состояния 4 начинается процесс изохорного перехода в состояние 5. Точность измерения показателя адиабаты
2 составляет только 0,1-0,3 секунды. Поэтому после состояния 2 порция газа некоторое время расширяется при постоянном давлении, переходя из состояния 2 в состояние 4 (см. Рис. 16), а по достижению состояния 4 начинается процесс изохорного перехода в состояние 5. Точность измерения показателя адиабаты  можно улучшить, если значение
можно улучшить, если значение  , соответствующее состоянию 3, определять из серии измерений при разных временах открытия клапана
, соответствующее состоянию 3, определять из серии измерений при разных временах открытия клапана  с помощью графической экстраполяции.
с помощью графической экстраполяции.